Introduction
This scenario provides uncertainty facing the XYZ Health insurance regarding the effects of adding the cost of premiums as a result of increasing standard of living because of recession and some risk factors that affects the amount of premiums that needs to be paid.
In order for the XYZ Health to determine the most reasonable increase that will be appropriate in order to avoid making the insured patients seek alternative medical options, it will be of essence for XYZ Health to use statistical analysis to determine the most appropriate premium additions that will aid in the decision making process.
The major aim of this analysis is thus to give reasonable estimates of using statistical tools based on the given data and other external factors to determine the most appropriate premium amount in dollars that will be reasonable for the XYZ Health to add without affection the decision making process of the insured people. Confidence level based on the mean, median and the standard deviation using SPSS will be appropriate in this case (Cooper, 2008).
Probability concepts
During the investigation of XYZ’s health insurance scheme, we looked at various methods of sampling data to come up with conclusive results to use in decision making. Various probability concepts could be used in this scenario, however we narrowed them down to these methods; confidence intervals, point estimates and Poisson distribution.
The probability concepts can be discussed as; the use of point estimates is applicable when it’s used to analyze a single number, in that it is limited to estimating up to a single figure, in this case a single amount like $40.While, confidence interval concept is a statistical method used to sample an array of diverse numbers or scores to come up with a level of accuracy and the figure is expressed in percentages.
Finally the Poisson distribution method is used in sampling the occurrence of various averaged numbers within a specified fixed time and if the occurrence of these numbers are time independent of the last occurrence. Poisson distribution method relies on probability of occurrences and is suited for scenarios which require speculation.
Due to the fact that XYZ sampled a small section of employees within the geographical are they operate; the probability concept that would be most appropriate to apply was the confidence interval method. This is because we were sampling various premium rates provided by employees, which they would comfortable with.
The use of the confidence interval method enables us to come up with a figure which estimates with high accuracy levels of the amount employees would be willing to increase to their insurance premium. Thus in this case confidence interval probability method would be the most suitable approach to use.
Statistical analysis
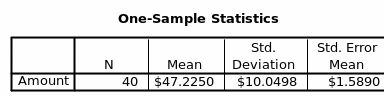
Based on the data given, statistical analysis to determine the mean, median, variance and standard deviation are done using spreadsheet and SPSS as shown below;
Mean
=$47.225
Median
The middle numbers are 48 and 49 hence
= (48+49)/2 =$48.5
Variance
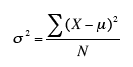
= 100.9994
Standard deviation
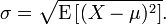
= $10.04984

As shown in the above calculations, the mean is about $47.225 and the standard deviation is about $10.04984 which shows that the dispersion about the mean which is $47.225 is about $10.04984, the standard deviation thus shows the minimum and the maximum amount of dollars that the sample group could tolerate before reaching the ‘breaking point’.
In order to appropriately determine the minimum and the maximum amount that XYZ Health can afford to add without affecting the clients commitment is determined more accurately using SPSS statistical tool.
As shown in the SPSS output, the 95 % confidence level is gained through determination of the maximum and the minimum amount of dollars that the clients are willing to tolerate without opting for other means of taking care of their health insurance. From the SPSS output, the minimum amount is about $44.01 and the maximum is about $50.44.
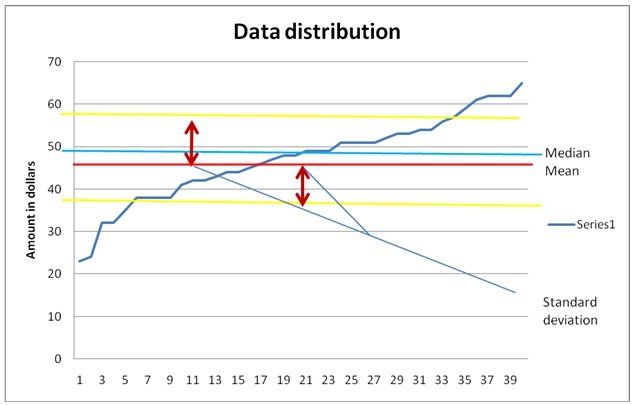
The XYZ Health can thus add amount between these two figures without affecting the perception or the decision making process of the clients. The figure presented here is based on the dispersion range from the mean which thus present 95 % confidence level. The data distribution above shows the ranges of data based on the standard deviation, the standard deviation marked by red arrows shows the ‘tolerable’ ranges which the clients will not be lost.
The maximum and the minimum amount based on the standard deviation are about $57.27 and $37.19, these values are within acceptable rates but the SPSS confidence level presents a more precise and accurate figure of about $44.01and $50.44.
Accuracy of probability concept
When using the various probability concepts we have to look and determine the accuracy and precision of using these methods. Accuracy and precision help an organization to come up with decisions which to a certainty will make them achieve their business goals.
With the use of point estimate method as statistical sampling technique, we arbitrarily come up with a certain amount to use as an insurance premium increase. This method is not an appropriate concept due to the fact that high accuracy and precision levels cannot be achieved (Lind, 2008).
In the case of Poisson distribution method being used in probability sampling, the accuracy and precision levels are high but they are not appropriate to be used in the scenario of XYZ Health Company. Poisson distribution method’s accuracy levels in this case would low in the range of 60-70%, owing to the fact that this method when used it is tied to occurrences of numbers or events in relation to time.
However XYZ Company’s insurance scheme is not to be implemented within a specific time range as the amount that agreed on will not be tied to the previous figures but due to sampled amount that matches the employees’ expectations.
Accuracy and precision levels with the use of confidence interval method are high and appropriate to this case. The accuracy levels with the use of this method range from 90 and 95%, this is because this method when used with sampled data, it calculates the confidence interval by using the mean (Broyles, 2006).
Confidence levels of 90% and above have fewer marginal errors in coming up with a desired figure or amount to be used, this is an advantage in that the organization will used results from the sampled data to come up with decisions which can be easily agreed to.
Recommendations
Based on the statistical data analysis, the premium rates should not exceed $50.44, this is the highest level that the premiums can be raised by XYZ Health without affecting its clients. The SPSS 95 % confidence level as calculated above supports this figure and hence useful for the firm decision making process regarding its addition of premium cost. The minimum figure that the firm needs to add is $44.01; this figure will provide an even more comfortable addition for most of the clients of the XYZ Health (Broyles, 2006).
I would therefore advice the XYZ Health to add at least $44.01 and not exceed $50, the rationale for this is purely based on the statistical 95 % confidence level which has projected that this range will be suitable for the XYZ Health to add without affecting the loyalty of the clients. The other imperative recommendation that I will give the company regarding the increase of premium is the need to cut down on the other costs through downsizing schemes in order to avoid passing on the overall cost to the customer.
Conclusion
As described in this analysis based on the statistical manipulations, the most suitable range for the XYZ Health to add on its premiums without affecting the response of the clientele is $44.01 to $50, this range provides what is statistically called 95 % confidence level. It is thus recommended for the insurance firm to base its decision making process on this statistics in order to maintain the clientele while trading off the increased cost which necessitated the increase of the premium rates.
On the other hand it is advisable for the firm to look for ways of minimizing the cost as a result of the external factors that the company has no control. One of such ways is company downsizing, this can be easily done to reduce the cost incurred by the company and enable the insurance firm to use the least addition to its clients.
References
Broyles, W. R. (2006). Fundamentals of statistics in health administration. Sudbury, MA: Jones and Barrlett.
Cooper, D. R., & Schindler, P. S. (2008). Business research methods (10th ed.). New York, NY: McGraw-Hill/Irwin.
Lind, D. A., Marchal, W. G., & Wathen, S. A. (2008). Statistical techniques in business & economics (13th ed.). New York, NY: McGraw-Hill/Irwin.