Introduction
Many of the physical quantities are direct or indirect functions of temperature. This means that as the ambient temperature increases, the value of the quantity in question changes: either upward or downward. For example, it is well known that solution viscosity and solubility of a substance have a strong positive correlation with heating, whereas, in contrast, the density of a substance tends to decrease with increasing temperature (Viscosity and density, 2019).
The temperature, in general, is one of the most understandable physical measurements because, although it is not tangible, its effect on bodies is not challenging to observe. The rise in body temperature, the warming of food, the melting of ice, and the weather are all literally everyday manifestations of temperature fluctuations. Given one’s intimate familiarity with the phenomenon of temperature, even without academic degrees, it can be postulated that this topic is one of the most accessible to explanation and discussion. This research report examines the superconductivity function of materials at high temperatures. This phenomenon is of great interest for theoretical and applied physics since the minimization of resistance to the electric field as the temperature rises is a valuable fact.
This paper discusses in detail the phenomenon of superconductivity of materials at high temperatures. This includes providing an evaluation of this phenomenon, an examination of its aspects, examples, and graphs revealing in more detail the dependencies discussed. The report will repeatedly use the names of superconductors written in the form of chemical formulas, as required by academic writing them. In addition, any temperature values to be provided in this report are on the Kelvin measurement scale. Ultimately, the report provides extensive, up-to-date material-gathering the most recent and fundamental knowledge on the topic of high-temperature superconductivity.
A Brief Background on the Phenomenon of Conduction
It is a well-known fact that when an electric field flows through a wire, the formation of a magnetic field initiated by the movement of charged particles inside a cylindrical wire is observed. In other words, the magnitude of the generated magnetic field is always equivalent to the current strength. The formula [1] clearly shows this relationship: when the value of current I increases, the magnetic field induction B increases, too. From a graphical point of view, if the current moves along a conditionally infinite cylindrical wire from bottom to top, then according to the right-hand rule, the magnetic lines of the generated field will form concentric circles with vector direction counterclockwise (Özdemir & Çoramık, 2018).
This relationship of the magnetic field with the current is critical and is constantly used in industries. Notably, one desirable area of manipulation [1] is to achieve high conductivity, or superconductivity, of materials, in which, due to the absence of resistance, the current traveling along the “wire” will have high stability and constancy, which in turn will lead to the creation of permanent magnetic fields (Ikram et al., 2021). In turn, such superconductivity cannot be achieved without temperature because it is a scientific fact that current resistance tends to zero only when the critical temperature reaches a specific value, set by the composition of the material of which the “wire” is made.
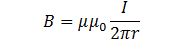
It is important to note that there is no strict connection between increasing the conductor temperature and achieving the condition of superconductivity. On the contrary, there is a unique value of the critical temperature point for each material, below which cooling leads to the appearance of high conductivity. Figure 1 shows some of the examples of super-high conductivity materials and indicates their critical temperature characteristic values. Consequently, using this figure as a source, one can confidently state that mercury has a critical point around 4 K — 4.1 K to be exact — and therefore the pure mercury material must be cooled to a temperature below this value to achieve its minimum resistivity conditions. This discovery is attributed to Heike Kamerling-Onnes, a Dutch scientist in the field of cryogenic temperatures (Bussmann-Holder & Keller, 2020). This works for other compounds as well, whose critical point is a known value.
History of Superconductivity Discovery
The value of Figure 1 lies not only in the worthy data provided on the critical points of each material but also in the ranking of these substances according to the chronology of the study of the phenomenon of superconductivity. More specifically, Figure 1 illustrates that Hg mercury is the first known material for which a critical point was determined in 1911 (Bussmann-Holder & Keller, 2020). One hundred ten years later, the number of refined critical points for materials has increased dramatically, and the number continues to grow. Even now, there are known cases of new, synthetic, or natural materials being discovered for which a good balance between an optimal critical point and high superconductivity is sought (Castelvecchi, 2020).
It is understandable that investing in cooling matter requires significant energy resources, so the fact that some of the available materials can also have high superconductivity at room temperature is industrially essential. As can be seen in Figure 1, for the first 70-75 years after the mercury critical point study, the academic community studied materials whose critical temperatures were below 30 K. During this period, a unified theory of superconductivity of materials by Bardeen, Cooper, and Schrieffer was formed (Zhou, 2019).
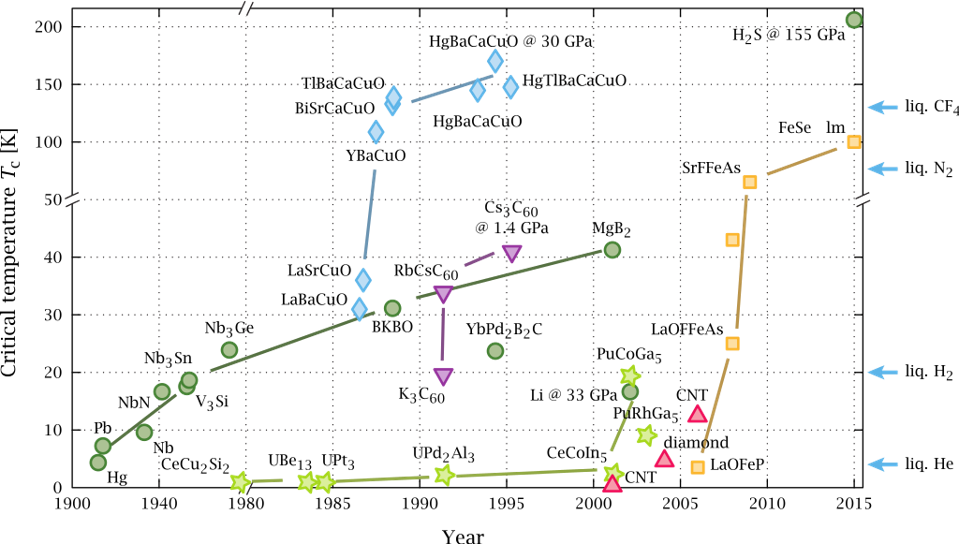
Created in 1957, the BCS theory (named after the authors) postulated that the particles that make up metals stop oscillating at extremely low temperatures because they no longer feel the pressure of thermal motion. Therefore atoms under such conditions can be considered virtually stationary. The BCS theory is inextricably linked to Cooper’s pair phenomenon: this effect is observed when valence electrons of metallic materials skip through positively charged atomic nuclei (Subedi, 2017). An excess positive potential is created during this process and forms the basis for in-line skipping and following electrons.
As a result, electrons migrate within the solid matrix in pairs to ensure the energy optimality of such movement. In turn, at ultra-low temperatures, all electrons form Cooper pairs: due to the high energy consumption for pair formation, electrons actually stop interacting with atomic nuclei, which from the outside can be regarded as slowing down of nuclei. To put it differently, the atomic nuclei of the conductor material now cannot slow down the electrons. Therefore, the latter can move virtually unhindered within the material matrix without experiencing any resistance: this phenomenon becomes the basis for the superconductivity of materials at low temperatures. BCS theory revolutionized the world of conductor physics by providing a microscopic understanding of how electrons interact with nuclei at lower temperatures.
Finally, the current milestone in the development of superconductor physics is tied, as seen in Figure 1, to the in-depth study of materials with a relatively high critical temperature. In this context, it is imperative to note what the term “high-temperature” means in conjunction with superconductors. In everyday life, it might seem that high temperatures are those parameter values that allow metals to red-hot or even melt. However, in the context of superconductivity, such a term does not mean such high temperatures but is generally limited to 30 K (Nishida, 2018; Palii & Belousov, 2021). In other words, reaching a temperature of 30 K (or -243.15 °C) is already sufficient to detect superconductivity phenomena in materials. In contrast, several authors suggest that the boundary condition is a temperature of 77 K (or -196.15 °C), which they associate with the boiling point of nitrogen (Miryala & Koblischka, 2018; Chigvinadze et al., 2019).
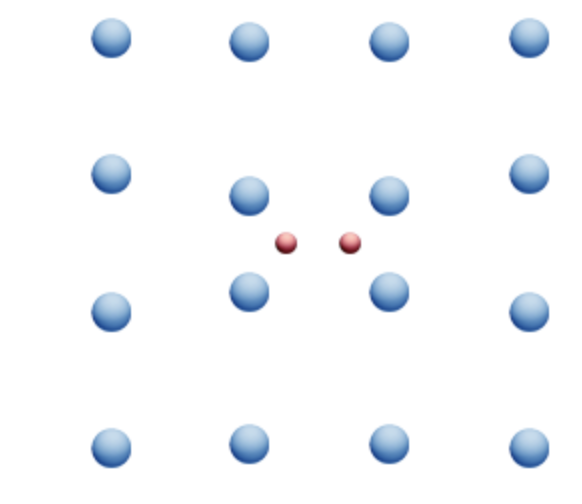
Another notable use of such “high-temperature” superconductors was their structure: unlike typical metals like mercury, niobium, or lead, high-critical-point superconducting materials tended to have a ceramic rather than metallic structure (Ikram et al., 2021). Most of these materials have a two-dimensional structure enclosed between oxygen-copper plates, as shown in Figure 3. It is essential that the generally accepted laws of conductive physics cannot yet explain the ability of ceramic materials to have such high conductivity in the absence of their characteristic metallic structure.
Properties of High-Temperature Superconducting Materials
It is important to note that superconductivity is realized in a stepwise rather than linear fashion as the material temperature decreases. If one refers to Figure 4, one can see that the resistivity of Bi4O4S3 increases dramatically when the temperature reaches 5.3 K, which is the critical transition point for this material (Hoshi & Mizuguchi, 2021). The same situation is achieved for all other conductors, and therefore one can conclude that the achievement of superconductivity conditions becomes possible only through a discontinuous movement. It is important to emphasize that the transition itself — as can be seen even from Figure 4 — takes place in the temperature range, and the size of this interval is the more comprehensive the more impurities the conductor contains.
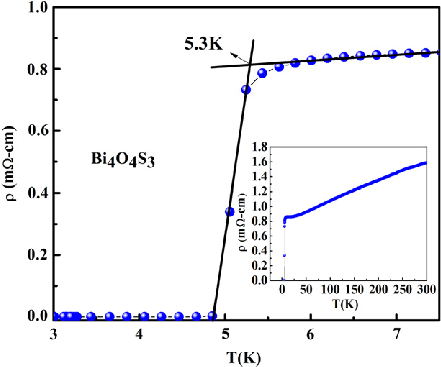
In addition, it is important not to identify the phenomenon of superconductivity only with the minimization of the material resistance. In reality, the achievement of such a state is also associated with a particular response of the conductor to the action of an external field: when a weak magnetic field (induction less than the critical value) acts on the conductor, it is completely pushed out of the body volume; this effect is called the Meissner effect (Parhizgar & Black-Schaffer, 2021).
More specifically, “inside” the superconductor, the magnetic field is wholly attenuated, and under these conditions, the body becomes a perfect diamagnet. The Meissner effect has a fascinating incarnation because as a result of achieving this situation, the magnet as a source of the external magnetic field appears to hover over the superconductor. This effect lies in the phenomenon of creating its own magnetic field: in fact, it is known that critical currents in the material can create its own magnetic field in the superconducting state. This, in turn, prevents the external magnetic field lines from penetrating inside the superconductor, which is observed as the neutralization of this field from the side. It is noteworthy that it is erroneous to say that there is no magnetic induction inside the superconductor at all since it is preserved only in the pre-surface layer, called the London depth (Torsello et al., 2019). Numerically, this value is defined as shown in equation [2].
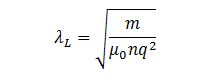
Peculiarities of New Superconductors
Turning again to Figure 1, it can be noticed an essential feature of all high-critical-temperature new-age superconductors. It is always a compound of several metals rather than pure elements since it is on the fact of synthesis that high synergy is achieved. However, with this phenomenon creates a significant problem — when trying to combine superconducting materials (or tapes) into a single complex, it is necessary to take into account the peculiarities of their geometry.
In particular, since it is crucial that the Cooper pairs pass from one superconductor to another, it is necessary to ensure a minimum gap between them. In fact, this gap should be so small that it does not exceed the size of a Cooper pair: it is talking about fractions of nanometers for YBCO-type materials. Failure to provide this size results in ceramic superconductors being unable to form stable magnetic fields due to the inability to pass critical currents. In other words, for industry, the lack of adequate clearance between crystals or superconductor grains becomes a threat to their practical use.
By now, there are several ways to solve this problem. One of the most obvious is to mechanically press the superconducting material to minimize grain spacing (Koch & Easton, 1977). Pressing produces superconducting thin ribbons of conductors: this formed the first-generation group of superconductors. Such materials are flexible and thin, have a silver hue, and can be used in industry, as shown in Figure 5. Despite the simplicity of obtaining such materials and the strategy of solving the problem of large grain spacing, first-generation superconductors are not entirely perfect. Their critical problem in such a case is the opposite effect: when the magnetic field caused by high superconductivity increases, the critical current transmittance drops rapidly (Yao & Ma, 2021). To put it differently, in the potential such conductors were effective only in the short term.
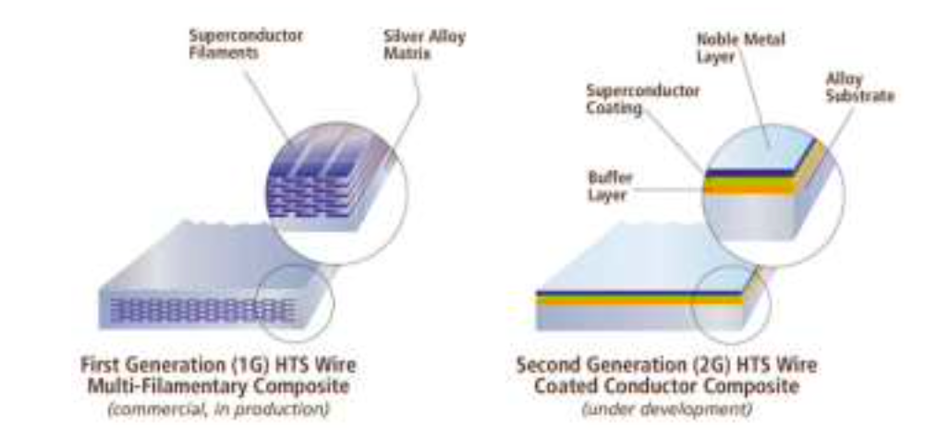
Another method of solving the mentioned problem is the creation of second-generation superconductors. Such materials were usually built using ReBCO as a conductor matrix (Yao & Ma, 2021). The peculiarity of the structure of the second-generation material is the use of a substrate, on which a thin nanoscopic layer of superconducting material is sputtered. The substrate is made uneven so as to set the direction of crystal growth. In other words, because of the given crystal growth vector, electron skipping is simplified because uniformity of the matrix is ensured. Although superconducting materials have the advantage to solve the previously outlined problems, there is still an essential threat to the mechanical strength of such compounds. In particular, as it is known, a magnetic field always tries to break an electromagnet, and extremely strong magnetic fields of several tens of Tesla are easily able to do this. As a result, second-generation superconducting materials are still fragile and cannot provide complete stability in use.
Superconductors in Nuclear Synthesis
One intriguing application of superconductors at high temperatures is in the fusion industry. In general, this area of the industry should be understood as the use of nuclear energy from reactive atoms to produce thermal and electrical energy (Galindo, 2021). The number of nuclear power generation plants worldwide is increasing, and the total contribution to global energy is projected to increase by 132 percent by 2050 compared to 2020 (Alves, 2021). The use of high-temperature superconducting materials in this industry has significant value. Unlike superconductors, which have low critical points, next-generation materials with extremely high critical temperatures allow for stronger critical currents, which in turn allow for more stable and stronger magnetic fields. It is well known that a stable magnetic field is the cornerstone of nuclear fusion, as it is what allows control of plasma confinement by large magnets in industrial machines (Shubov et al., 2021). To put it another way, high-temperature superconductors are critical to the energy optimization of nuclear reactors.
However, it is fair to point out that such technologies are still quite unreliable, as some problems cause difficulties in implementing revolutionary ideas. In particular, as noted earlier, the high-critical-temperature materials of most interest for nuclear power have a brittle ceramic structure, which means that their use is more complicated. In response to this challenge, laboratories worldwide are trying to find a good compromise between superconductivity and material strength by forming new compounds. One of these is YBCO, a mixture of yttrium, barium, and copper oxide (YBa2Cu3O7-x), whose transition temperature to the superconducting state is 93 K (Hasan et al., 2021).
It is essential that YBCOs can be modified by replacing some metals with others. For example, ReBCO is a compound where yttrium can be replaced by any rare-earth element, such as gadolinium (Iannone et al., 2020). In particular, one use of YBCO is to grind the material into powder and fill metal wires, which can then be coiled onto toroidal solenoids to achieve a stable magnetic field with the highest values of magnetic induction.
Conclusion
To summarize this review, it is essential to emphasize that superconducting materials are some of the most interesting physical bodies that find extremely high applications in industry. High-temperature superconducting materials are those bodies whose critical points are above 30 K or 77 K in different interpretations by different authors. When the temperature of these bodies drops below this value, high superconductivity is formed in them due to the formation of a Cooper pair. As a consequence, the nuclei of such materials have almost no effect on the electrons, and therefore their internal resistance tends to zero. This is important for the industrial industry, because in this case, the passage of critical currents through superconductors allows the creation of stable magnetic fields of great strength. The report showed that one such application of this effect is nuclear fusion, which, in turn, is critical for the energy industry. Modern research on high-temperature conductors continues, as fundamental problems of mechanical strength and the search for an optimal balance are still to be solved. The number of such materials is expected to increase in the near future.
References
Alves, B. (2021). Global outlook on electricity generation by energy source 2018-2050. Statista. Web.
Bussmann-Holder, A., & Keller, H. (2020). High-temperature superconductors: underlying physics and applications. Zeitschrift für Naturforschung B, 75(1-2), 3-14.
Castelvecchi, D. (2020). First room-temperature superconductor excites — and baffles — scientists. Nature. Web.
Chigvinadze, J. G., Ashimov, S. M., Acrivos, J. V., & Gulamova, D. D. (2019). Critical temperature of the superconducting transition of individual phases of bismuth multiphase cuprates after cooling in a magnetic field to a temperature of 77 K. Fizika Nizkikh Temperatur, 45(4), 447-456.
Czerwiński, D., & Jaroszyński, L. (2005). Circuit model for current leads made of HTS tapes. Web.
Galindo, A. (2021). What is nuclear energy? The science of nuclear power. IAEA. Web.
Hasan, N., Hafeath, H., & Ahmed, A. (2021). Synthesis and characterization of the bulk YBCO-target of superconducting material. Materials Today: Proceedings, 42, 2268-2272.
Hoshi, K., & Mizuguchi, Y. (2021). Experimental overview on pairing mechanisms of BiCh2-based (Ch: S, Se) layered superconductors. Journal of Physics: Condensed Matter, 33, 1-18.
Iannone, G., D’Agostino, D., Saggese, A., Celentano, G., & Gambardella, U. (2020). Quench propagation in commercial REBCO composite tapes. Cryogenics, 109, 1-6.
Ikram, M., Raza, A., Altaf, S., Rafi, A. A., Naz, M., Ali, S.,… & Haider, J. (2021). High temperature superconductors. Transition Metal Compounds: Synthesis, Properties, and Application, 8, 57-74.
Koch, C. C., & Easton, D. S. (1977). Mechanical behavior and stress effects in hard superconductors: A review. Web.
Miryala, M., & Koblischka, M. R. (2018). High-temperature superconductors: occurrence, synthesis and applications. Nova Science Publishers, Inc.
Nishida, M. (2018). The mystery of cuprate high temperature superconductors. Web.
Özdemir, E., & Çoramık, M. (2018). Reasons of student difficulties with right-hand rules in electromagnetism. Journal of Baltic Science Education, 17(2), 320-330.
Palii, N. A., & Belousov, O. K. (2021). Magnesium compounds as future high temperature superconductors. Journal of Physics: Conference Series, 1758(1), 1-5.
Parhizgar, F., & Black-Schaffer, A. M. (2021). Diamagnetic and paramagnetic Meissner effect from odd-frequency pairing in multiorbital superconductors. Physical Review B, 104(5), 1-11.
Patel, P. (2021). What are Cooper pairs & how are they responsible for superconductivity? Science ABC. Web.
Siegel, E. (2021). How close are we to the holy grail of room-temperature superconductors? Forbes. Web.
Shubov, M. (2021). Energy balance within thermonuclear reactors. Web.
Srivastava, P., & Patnaik, S. (2013). Evidence for fully gapped strong coupling s-wave superconductivity in Bi4O4S3. Journal of Physics: Condensed Matter, 25(31), 1-5.
Subedi, M. S. (2017). Superconductivity and Cooper pairs. Himalayan Physics, 6(7), 104-107.
Torsello, D., Cho, K., Joshi, K. R., Ghimire, S., Ummarino, G. A., Nusran, N. M.,… & Prozorov, R. (2019). Analysis of the London penetration depth in Ni-doped CaKFe 4 As 4. Physical Review B, 100(9), 1-7.
Viscosity and density. (2019). BYJU’S. Web.
Zhou, T. (2019). Mechanism of high temperature superconductivity-the BCS theory and a new electron pairing medium. Web.
Yao, C., & Ma, Y. (2021). Superconducting materials: Challenges and opportunities for large-scale applications. Iscience, 24(6), 1-13.