Electromagnetic Wave Propagation in the Stratified Medium Term Paper

Background

Electron interactions with the periodic ionic lattice modify wave functions, causing band gaps in the allowed states’ spectrum. This article presents electromagnetic wave propagation in the stratified medium that generalizes and simplifies the usual two-by-two matrix analysis. Through the presentation, the author demonstrates infinite periodic band structures’ implications for finite structure reflection and the universality of some reflectivity features, which was discernible in the early days of quantum mechanics. For example, while Isaac Newton examined the properties of elastic waves on a single-dimension lattice of spring-connected masses as a sound model, Rayleigh recognized stop band possibilities for periodic structure waves in relation to stratified medium’s high reflection. However, it was the French physicist Florin Abelès who advanced stratification’s modern optics.

Electromagnetic Waves in Stratified Medium

In developing the equation for wave propagation through a stratified medium, it is important to consider the nature of that stratification. Possible forms of stratifications include planar stratification, characteristic matrix, and a stack of discrete layers (Born & Wolf, 2013). For planar stratification and the propagation of light through this medium, one assumption is that a linearly polarized electromagnetic wave (such as light) travels through it. Because the wave is linearly polarized, it is a transverse (TE) electric wave.

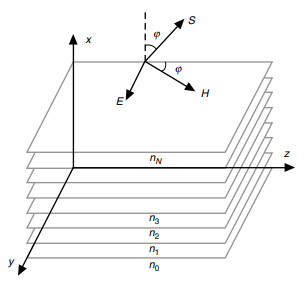
From Figure 1 above, the assumption is that an electromagnetic wave with a y-axis linear polarization is propagating through the medium. As seen in the picture, H is in the xz incidence plane alongside the S pointing vector, while E remains parallel to the y-axis. The y-direction invariant wave’s incidence angle is φ. Because the medium is stratified, a constant refraction index’s planar surface is perpendicular to the x-axis. Regarding their extent, the surfaces are infinite and parallel to the yz-plane. Therefore, it would be adequate for one to consider TE’s case and its xz-plane propagation as the starting point for the comprehension of the movement of electromagnetic waves through a stratified medium.

Notably, there are many reasons for analyzing the transverse electric case as the starting point. The resulting equations are simpler for TE waves through a medium where µ ≡ 1 than for the transverse magnetic (TM) waves involving the same medium. Obtaining results that are adequate for the transverse magnetic (TM) case requires the utilization of a mathematical description of the H, which is obtained from treating the TE case and combining it with Maxwell equation’s symmetry property. The noteworthy point is that Maxwell’s equations remain unchanged even with the simultaneous exchange of field vectors and their medium parameters according to the transformation. If from the TE case, one derives the value of H, then they can obtain E for the TM case.

In a planar wave’s plane of incidence (i.e., the xz-plane) for a TE wave, the curl equation is E_x = E₂ = 0. In Maxwell’s equation for a TE harmonic wave, the curl relationship gives:

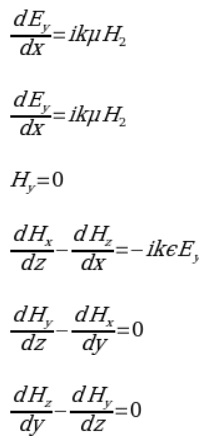
Where H_y≡ 0 and H_x, H_2, and E_y are functions of x and z only. From the equations above, the TE case’s electric field’s time-independent component must satisfy the Helmholtz equation given by:

We the technique for variable separation, one can set

as a trial solution. Then,

becomes:

Where the left side of the equation above is an x only function while the one on the right is a z only function. The assumption holds only when both the right and left sides of the equation above are constant. As such;

Since the solution for Z(z) is given by , then the z direction’s wave’s time-independent component’s phase accumulation rate is given by kn₀, and is invariant for a particular wave. Assuming, without generality’s loss, that the wave is moving rightwards from left, i.e., in positive z’s direction, one can adopt the positive sign in

, allowing the derivation of the harmonic wave’s electric field by:

From Maxwell’s equation

, the expression of the components of the magnetic field is in terms of x’s different functions but z and t’s similar functions, given by:

Another condition needed for the wave function to hold is that the U, W, and V functions satisfy specific requirements among themselves. From equations

,

,

,

,

, and

, these conditions are given by:

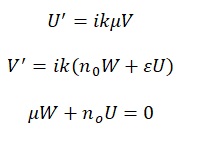
If one eliminates W, they get, for U and V, first-order differential equations’ coupled system given by

and

. It is possible to convert these two systems into two independent second-order differential equations. For the TM case,

, the transformation

yields

It is notable that for the TE case, U, W, and V are complex. Thus, from

, one can define the cophasal surface (a surface for E’s constant phase) by

, where ψ(x) is U(x)’s phase. The angle of incidence (φ) that the cophasal surface has with plane yz in Figure 1 is given by

. in special cases when the electromagnetic wave remains planar, then

From this, it follows that the constant in

is also equivalent to n₀ = nsinφ = constant, which is Snell’s law. Thus, one can consider the condition from the solution to

is Snell’s law generalization. The turning point for the wave is given by the value n₀, which remains related to Figure 1’s 0^th layer’s index of refraction and the layers in which φ = π/2; the wave’s turning point.

For the TM case, consider an electromagnetic wave hitting a nonmagnetic planar stratification from a medium of index n₁. The local value of the refractive index of the stratified planar surface is given by the dielectric function ∈(z) = n²(z)[(z). Given an isotropic medium with scalar (not tensor) dielectric function, one can write any plane wave as a transverse electric (TE) and transverse magnetic (TM) waves superposition (TE is also called the s wave and TM the p wave). The s wave’s electric vector is perpendicular to the incidence plane and p wave’s electric vector is perpendicular to the incidence plane. Assuming medium stratification in direction z, such that ∈ = ∈(z), and given that the incidence plane is (z,x), then the electric field vector of the s wave is E = (0, E_y, 0) and the magnetic field vector of p wave is B = (0, B_y, 0). From the curl equation by Maxwell, it follows that, if ω is the angular velocity, then:

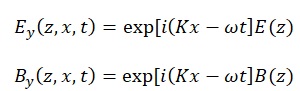
Where K is a separation-of-variables constant implying Snell’s law. Notably, K’s existence derives from the stratification’s planar nature. Both the E(z) and B(z) functions fulfill the ordinary differential equations:

Where q(z) is the wave vector’s nominal component’s local value given by:

Assuming that the incidence angle is 0₁, then:

Where 0₂ is the angle between the wave vector and the normal in the homogenous substrate of index n₂. Notably, from the foregoing, dE/dz and

remain continuous where ∈(z) has any discontinuity. If this was not true, delta function terms would become available in the second derivative of

. E and B are a fortiori continuous at any ∈(z) discontinuity.

If a stratification extends from z = a to z = b, bounded by the homogeneous indices n₁ and n₂ , and if ∈(z) is initially continuous for a<z<b, and if F(z) and G(z)

are s wave’s two linearly independent solutions of the differential equation

, then one may write E(z) as F and G’s linear superposition as: E(z) = f F(z) + g G(z) where f and g are constants. The approach has proven useful in calculating light propagation through a thin film with Cartesian stratification.

In the ordinary approach to the examination of light propagation through thin film, individuals initially treat the stratified medium as a multilayered one. Here, one must hold constant the index of refraction within each layer, although changes across boundaries are permissible by some finite number multiplied by the layer’s thickness. Notably, the finite number may correspond to the neighboring layer’s average gradient. However, things appear different within each layer because one can solve the wave equations using sinusoid functions. Maxwell equation’s continuity conditions enable one to connect solutions from adjacent layers together and across their boundaries. After that, one can drive each layer’s maximum thickness to zero, allowing the layers’ number to expand indefinitely such that the medium’s total thickness remains unchanged. From the ensemble of answers, the resulting estimated one can give an accurate description of the electromagnetic field propagating through the medium, provided that the “thin atmosphere” condition is true and the wave does not experience a turning point.

Reference

Born, M., & Wolf, E. (2013). Principles of optics: Electromagnetic theory of propagation, interference and diffraction of light. Elsevier.