Optics: The Experiment of Snell’s Law Research Paper

Introduction

Light travels in a straight line in a given medium and at a specific speed. The speed varies from one medium to the other depending on its make (Bend 3). When light strikes a smooth surface at an angle (angle of incidence), it is reflected back at an angle (angle of reflection). Light can also “proceed to the next medium at a different angle (angle of refraction), and this depends on refractive indices of the media involved” (Dudley 12). With refraction, light deviates from its initial path as it traverses the interface of two media. The degree of bending is proportional to the refractive index of the medium. Each medium has a different refractive index denoted by n. The refractive indices for some common substances under room temperatures are given in the following table:

Table 1: A table showing refractive indices of materials (Wolf 56)

With the knowledge of the refractive index of air, it is possible to calculate the refractive indices of other materials. In essence, with an incident ray traversing two media with different refractive indices, the incident ray, the normal to the interface separating the two media and the refracted ray intersect at a common point and occur on a common plane. If light travels from a medium with lower refractive index n₁ to another medium with a higher index n₂, it is bent towards the normal and vice versa (Dudley 12). Mathematically, the angle of incident and that of the refracted ray are connected by the equation n₁ *sin θ₁ = n₂*sin θ₂. This represents the Snell’s Law. As such, n₁ and n₂ represent the refractive indices of the media in question with θ₁ and θ₂ representing the angles of incident and refracted ray respectively.

Snell’s Law holds where the angle of incident does not exceed the critical angle (C) when the refracted ray is 90^o (Boilen 34). Beyond C, whatever happens is total internal reflection. In this report, the main objective is to ascertain the authenticity of Snell’s Law.

Experimental Systems

The experimental apparatus include optical accessories (glass block -parallel slab), sheets of white paper, ruler, protractor, pencil, soft board and safety pins.

Experimental Methods

In this experiment, the outline of the glass block was traced on a white piece of paper that was secured on a soft board. The block was removed and using a protractor; a normal was drawn on one side (long) of the outline. An angle θ_i (10^o) was then measured, and a line drawn using a pencil before the glass was replaced. Two safety pins were then placed perpendicularly above the line. While observing from the opposite end of the block, two other pins were placed to coincide with the initial two on the opposite side (see below). The glass block was then removed, and a line was drawn and produced joining the two pins to meet the outline. At the point of intersection with the outline, a line was drawn to meet the other line. The angle (θ_t) “was measured and recorded (see below)” (Dudley 12). This was repeated for θ_i = 20^o, 30^o and 40^o. A graph of sin θ_i against sin θ_t was then plotted for analyses.

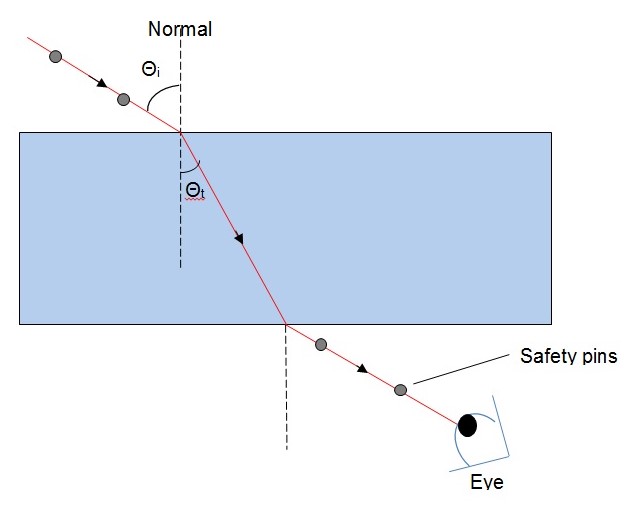
Theoretical model

According to Snell’s Law, n₁ *sin θ₁ = n₂*sin θ₂. But since our reference medium 1 is air (n=1) then it follows that:

sin θ₁ = n₂*sin θ₂ ( since n₁=1).

This equation is in the form of y = mx; where m = n₂ which is the refractive index of the second media. In this case, a graph of sin θ_i against sin θ_t yields a straight line with gradient equivalent to the refractive index of the glass (1.523).

Results and discussion

Table 2: showing the angles of incident plus their respective angles of refraction

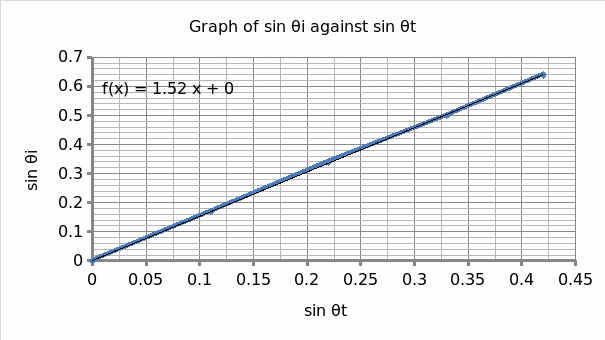
In this experiment, the authenticity of Snell’s Law was tested. As per this law, a plot of sin θ_i against sin θ_t would result in a straight line that passes through the origin with the slope representing the refractive index of the second media (glass =1.53). From the results above (figure 2), the experiment produced credible results though the best line of fit didn’t pass through the origin. This could be attributed to interference due to the reference medium (air). This could be averted in the future experiments by using the vacuum as the reference medium, and when performed under standard temperature condition. Also, white light is subject to interference, yielding incredible results. These are some of the uncertainties that culminated in the deviation of the resulting refractive index of glass (1.518). Future experiments ought to explore monochromatic (sodium D) as an incident ray to avoid interferences due to dispersions.

Conclusion

In this experiment, the results echoed Snell’s Law, which predicts a linear relationship between sin θ_incident and sin θ_refractive with the gradient representing the refractive index. However, the resulting refractive index (1.518) was not accurate for glass due to experimental errors. Future experiments should consider performing the experiment in a vacuum and using monochromatic (sodium D) light to obtain accurate results.

Works Cited

Bend, Glassner. An Introduction to Ray Tracing. Boston: Alley, 2000. Print.

Boilen, Marten. Refraction and reflection at a metal surface. New York: Penguin, 2006. Print.

Dudley, John. Physics World. Denver: MacMurray, 2003. Print.

Wolf, Brian. Geometry and dynamics in refracting systems. Denver: MacMurray, 1995. Print.