Utilization of Space and Time in Design Research Paper

Introduction

Generally, design entails planning for the construction of systems or objects. These include engineering drawings, circuit diagrams, and architectural blueprints. There are several connotations in various design disciplines such as architecture, planning, engineering, and other technological disciplines. Design, therefore, is defined as, “a strategic approach by individuals or roadmap to achieve a certain unique expectation.” It caters to parameters, activities, plans, processes, costs, and all that should be done within the environmental, political, economic, legal, social, and safety constraints to the objective (Lacey 318). Such is the wide denotation of design that there exist various approaches and philosophies towards design. For structural design, time, and space aspects from Newtonian physical equations of motion is a fundamental framework. Although there are several approaches to achieving the design frameworks, actually, Newtonian laws of motion of space and time are the basis of structural designs.

Newton’s equations of motion

There are three Newton’s equations of motion in basic classical mechanics all of which obey Galilean relativity. However, the equations do not obey Einstein’s principles of modern physics relativity hence effect of length contraction and/or speed of light barrier is not applicable in situations where the equations are used for deduction of principles.

First Newton’s equation of motion

“Consider a body that has travelled a distance x in time t. The velocity v of the body is given as the rate of change in displacement

V=x/t

If the body is travelling at an initial velocity of u and changes velocity to v within a given time t, then the acceleration of the body is defined as; rate of change in velocity and becomes

a = (v-u)/t (1)

Equation (1) assumes that the acceleration of the body is uniform throughout the given time period” (Lacey 337). Rearranging the above equation:

a= (v-u)/t

at = v-u

v-u = at

v= u + at (2)

Equation (2) is the first Newton’s equation of motion.

Second Newton’s equation of motion

Generally, objects move with uniform velocity, uniform acceleration or non-uniform acceleration. If a body is moving with a uniform velocity v, the total distance travelled s, in a time t is given as

V=s/t (3)

Equation (3) implies s=vt (4)

For a body under uniform acceleration, with the initial velocity u and velocity after time t given as v, average velocity is calculated as:

Average velocity= (u+v)/2

From equation (4),

s= {(u+v)/2} t (5)

Substituting equation (2) in equation (5), we get:

s = [(u+u+at)/2] t

s = [(2u + at)/2] t

s = [(u + (1/2) at)] t

s = ut + (1/2)at² (6)

Equation (6) is the second Newton’s equation of motion.

Third Newton’s equation of motion

In order to have an equation, which relates the final velocity of a body v and the distance travelled s, we use equation (2) as follows:

v=u+at

v² = (u+at)²

v² = u² + a²t² + 2uat

v² = u² + 2uat + a²t²

v² = u² + 2a(ut + (1/2)at²) (7)

Replacing equation (6) in equation (7), we get:

v² = u² + 2as (8)

Equation (8) is the third Newton’s equation of motion.

Space and time Newton’s equations of motion and design

Newton’s equations of motion play a prominent role in the design discipline and several areas of science and technology. This arises whenever there is a need to determine a relationship that involves some quantities that are continuously variable and their rates of change in space and/or time are known (Lacey 319). This is illustrated in situations where the motion of a body under design is described by its position and velocity as time varies. By applying Newton’s Laws, one is able to relate the position, velocity, acceleration and the various forces acting on the body and state. There are several examples of modeling Newtonian equations of motion into real-world applications of machines and objects. A ball falling through the sky, a rocket shot into space, amusement parks are just but a few to mention. In this paper, I will show in detail the effects of equations of motion in time and space on a rocket hence the significance in its actual design.

Discussion

Newton’s third law of motion states that “for every action, there is an equal and opposite reaction” (Lacey 338). The motion of a rocket is based on this principle. The ignited rocket propellant burns at very high temperatures and accelerates out of the rocket by squeezing through the small nozzle at the back. The exhaust produces an equal reaction force in the opposite direction which propels the rocket forward. The time and space equations governing this motion are as described below.

“To comprehend the concept properly, the application of the principle of momentum and impulse to a given system is necessary. We then use calculus to set up the governing equations of time and space” (DiSalle 92). Consider the rocket below moving in a vertical direction and in two states; stage 1 when the system is at time t and stage 2 when the system has moved an infinitesimal time dt hence is at time t+dt as shown below (“Rocket Physics” 1). This leads to the following conditions:

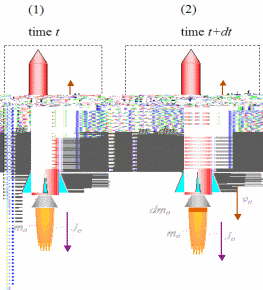
“m = mass of the rocket (including propellant), at stage (1)

m_e = total mass of the rocket exhaust (that has already exited the rocket), at stage (1)

v = velocity of the rocket, at stage (1)

J_e = linear momentum of the rocket exhaust (that has already exited the rocket), at stage (1). J_e is constant between (1) and (2)

dm_e = mass of rocket propellant that has exited the rocket (in the form of exhaust), between (1) and (2)

dv = change in velocity of the rocket, between (1) and (2)

v_e = velocity of the exhaust exiting the rocket, at stage (2)

The ground is our inertial frame of reference hence all velocities are measured with reference to it. Upward direction motions are considered positive and downward motions negative” (DiSalle 93). “We will also assume that the rocket is moving in a vacuum space hence neither air resistance nor gravity affects its motion. During the transition from stage 1 to the stage 2, there is an upward change in linear momentum due to the resultant external upward force acting on all the particles in the system” (DiSalle 94). This is expressed mathematically using equations of motion as below:

Where ΣF_y = the total external upward forces acting on all particles in the system (rocket + exhaust).

Expanding the above expression, we take the limits as dt→0 and neglecting the “second-order” term dm_edv. Dividing by dt and simplifying, we get:

Since gravity, and air resistance (drag) is negligible, ΣF_y = 0 as no external forces act on the system. Equation (1) above then changes to

Since a = dv/dt is the acceleration of the rocket, and according to Newton’s second law, ΣF = ma. The rocket thrust T is therefore mathematically represented as:

v+v_e = velocity of exhaust burning propellant gases. This velocity is approximately constant and is measured relative to the rocket. dm_e/dt = the rate at which the rocket propellant burns (“Derivation of Newton’s equations of motion” 1).

The rocket acceleration increases with the burning propellant, which reduces its mass. Maximum acceleration therefore is at the instantaneous moment when the propellant burns off for any given value of thrust T.

From equation (2),

This becomes

Mass of exhaust ejected by the rocket is equal to the negative mass change of the rocket hence

This implies

Using calculus to integrate the equation above and simplifying using u = v+v_e, we get

The equation we have come up with is very significant in the analysis of rocket physics. The variables in the equation have the following meaning: v_i is taken as initial rocket velocity. m_i = initial mass of the rocket. m= the mass of the rocket at any time t when the rocket is in motion and v= the velocity of the rocket. It should be noted that irrespective of the initial velocity v_i, the change in velocity (delta-v) is always constant (Reichenbach 289). This is very significant in such times when the speed of rockets is increased by powered gravity assist which entails acceleration of a rocket during the periapsis stage. The result is the maximization of the final kinetic energy and velocity of the rocket.

Consider the analogy of an elastic ball dropped on the floor by an observer so that it bounces back upwards upon hitting the ground. In order for the ball to bounce back with maximum velocity, its velocity must be increased by a constant dv at a time t when the ball is in flight. This means it will also have the highest possible kinetic energy. From the discussion equations above, this time t is the last moment prior to the ball hitting the floor. The increase in velocity increases the total energy of the ball to the maximum. On the rebound, maximum kinetic energy and velocity are achieved. Comparing the dropping ball to the rocket, the velocity achieved at this time t, therefore, is comparable to the velocity of the rocket when all the propellant fuel has just finished burning.

Conclusion

Design on a broader aspect is a necessary need without which major and minor projects would not get off the ground. There are several connotations and philosophies of desigingn each of its own ideologies with pros and cons covering vast aspects of life. As discussed above, there are three major Newtonian equations of space and time. Newton’s equations of motion for space and time are fundamental in the design of various objects in engineering structures. There are other ideologies for other forms of designs as the discipline is broad. The actual principle applied by an individual depends on the area of design. The Newtonian equations analyzed in this paper for the thrust of a rocket are a demonstration of the significance of space and time utilization in design. We can therefore conclude that Newtonian laws of motion for space and time are a basis of structural design.

Works Cited

Derivation of Newton’s equations of motion. 2002. Web.

DiSalle, Robert. Newton’s Philosophical Analysis of Space and Time. New York: Cohen and Smith, 2002. Print.

Lacey, Hugh. “The Scientific Intelligibility of Absolute Space: A Study of Newtonian Argument,” British Journal for the Philosophy of Science, 21(1970): 317–342. Print.

Reichenbach, Hans. The Philosophy of Space and Time. New York: Dover Publications, 1958. Print.

Rocket Physics. 2012. Web.