Background Information on Behavioral Differences of Mutual Fund Managers
Algorithmic Trading and Mutual Funds
It should be stressed that algorithmic trading is frequently used by mutual funds because it allows the managers to calculate securities in large amounts with the help of sophisticated mathematical formulas. In particular, this form of trading includes the division of larger amount of shares into smaller groups to provoke quick selling and buying.
Therefore, algorithmic trading is used by mutual funds to successfully manage opportunity cost, market impact, and risks (Bergan and Devine, 2005). Automated trading is also used to initiate orders premised on date received electronically to define such aspects as timing, price, and final income.
With regard to the above-presented considerations, Chaudhuri (2004) and Khnadani and Lo (2007) state that algorithmic trading enable the mutual fund managers to identify whether their profits can be forecasted in terms of risks and returns obtained at mutual funds.
Particular role in defining the connection will be played by random and autoregressive models proposed by Friedman and Shachmurove (1997) for defining the future values of mutual fund performance. Beside greater accuracy of prediction, the risk adjustment rate can be calculated in a less time consuming mode providing more valid results.
Impact of Algorithmic Trading on Tournament Behavior
It has been commonly recognized that processes of forecasting and modeling are intrinsic, challenging, and fluctuating. These processes are closely associated with a random walk process implying that these correlation series are statistically and economically insignificant (Malkiel, 2003).
Such an assumption is premised on the studies of Eugene Fama (1970) who believes that stock markets were significantly efficient in presenting data about individual stocks and about stock market in general. With regard to this theory, there is a close relation between the information available and the extent to which future outcomes are predictable.
However, financial researchers and statistics are more inclined to believe that stock prices as well as returns are to an extent predictable (Malkeil, 2003). In particular, Adaptive Market Hypothesis has emerged in an effort to reconcile behavioral and predictable models of stock prices identification.
Introduced by Andrew Lo (2004, 2005), the concept applies evolution principles , those of adaptation and natural selection to financial operations. Predictability of mutual fund returns can be analyzed from different perspectives. On the one hand, predictability enables investors to earn extra returns whereas unpredictable processes prevent them from achieving this goal.
One the other hand, results base on predictability do not necessarily imply that profits is connected with unfavorable risk; at the same time, unpredictable calculations can lead to profit if their expected risk is favorable (Hallahan et al. 2009). One way or another, the estimated results are uncertain because the forecasting is based on measuring the extent of uncertainty.
This means that probability theory should be introduced to define the number of probability to each particular event where the highest certainty is applied to number 1 (Lo, 2004). The assessment of probability level is aimed at achieving Sharpe ratio that reveals the way the return compensates the risk taken. In this respect, the higher the ration is the more return is obtained for the same risk, in case risk free rate benchmark is a constant.
The above information presents how scheme according to which expectations are identified. In this respect, Khandani and Lo (2007) and Chaudhuri (2004) believe that short-term mean reversal model of algorithmic trading allowing the mutual managers to define whether their profits can be predicted with reliance on random model of forecasting accuracy of risks and returns at mutual funds.
Methodology
Before applying specific algorithmic trading models, it is necessary to state that “fund managers who are interim losers are likely to increase fund volatility in the latter part of the assessment period to a greater extent than interim winners” (Hallahan et al., 2009, p. 14).
This tournament behavior can be predicted within the risk adjustment ration (RAR) model: (σ2L/σ1L)>(σ2W/σ1W) (1), where σ1 and σ2 are identical to the portfolio risk levels at the first and the second stages correspondently. L and W letters refer to lose and winner respectively. The presented equation provides a solid basis for further analysis and prediction of tournament behavior in mutual funds with the help of algorithmic trading models (Alonso, 2010).
As it has been mentioned before, computational tools contribute greatly to the analysis of risk-return ratios based on a risk shifting behavior. In case the risk is not a constant indicator, the Sharpe ratio will look as follows:
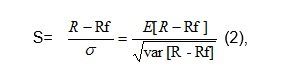
where R is the return the investor will get, Rf – free rate risk, and σ – is fund volatility. With regard to the assumptions made by Alonso (2010), Fama (1970), and Friedman and Shachmurove (1997), free rate risk can undergo shifts in the course of time.
Consequently, algorithmic trading, particularly linear autoregressive model, can provide more accurate results while presenting calculations of predictability and changing values of stocks in future (Wilson and Banzhaf, 2010).
First stage regression, therefore is needed to evaluate the amount of the information obtained: Mit=αi+۷i+βQit+εit (3), where Mit is dependable variable, Qit is the autoquote set, αi is fixed effect on stock and ۷t is a set established per day (Hendershott, Jones, and Menkveld, 2011).
Tournament behavior also presupposes regime switching, which is strictly adhered to Adaptive Market Hypothesis proposed by Lo (2004, 2005). Tournament behavior of mutual funds, therefore, is often predetermined with the desire to predict those switches and gain a competitive advantage.
In this respect, algorithmic trading models and strategies can assist in defining achieving the highest Sharpe ratio with the help of high-frequency trading (Butler, 2007). This approach is quite effective if attached to the Sharpe ration because the more bet the mutual fund manager place, the smaller standard deviation from the mean they will experience.
Another theory of algorithmic trading is Game theory that is applicable to capturing behavior in making specific choices (Alonso, 2010; Aumann, 1987). Being initially introduced for evaluating competitions where one individual is competitively stronger than another, the model contributes to better understanding of changing prices in the efficient market.
The model for understanding the changing behavior is simple. For instance, if the rise today is higher than the expected rise, than it is predicted that the rise tomorrow will be lower than the rise today. The probability model can be presented as follows: 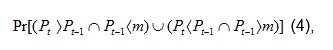
where Pt is the rise per a particular unit of time, which is an independent variable (Alonso, 2010). Hence, the two unite events embracing the probability statement are associated with the action defined in informal prediction model presented above.
While moving on with the analysis of spread and probability, high frequency model is placed within the context of presenting risk management techniques and trading rules.
With reference to trading rules, it is imperative to consider the marketing position in pair that enables to avoid magnitude of mean reversion and minimize the standard deviation. Hence, we should choose a return rate and portfolio weights to diminish the overall fluctuation of the portfolio (Chiu et al., 2011; Gatev et al., 2006). All these calculation can be presented in accordance with Markowitz model:
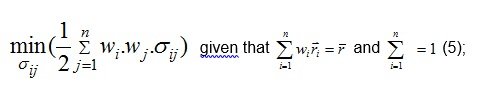
While presenting a pair selection scheme, it is imperative to analyze those pairs for stationarity and reversion. In order to assess the risk taken by mutual fund manager, it is necessary to avoid market risk through presenting pairs of assets as ∆β≤0.1 (Chiu et al. 2009, p. 6).
The pairs will be selected from the same sectors to avoid misconception and industry risk. Here the main risk encountered by managers is regime switching (Alonso, 2010). In other words, the pairs spread no longer takes place and the time span for mean reversion has been radically changed.
Conclusion
The above presented models offered by Alonso (2010), Chui et al. (2009), Hendershott, Jones, and Menkveld (2011) contribute greatly the analysis of tournament behavior of mutual fund manager in terms of timing, risk management, and liquidity.
The theories proposed by Aumann (1987), Lo (2004, 2005), and Wilson and Banzhaf (2010) are greatly elaborated by above-presented computational tools. In particular, the reliance on autoregressive model and reversion mean support the theory offered by Fama (1970) about the risk-changing behavior at the investment market.
Reference List
Alonso, N. M. (2010). Statistical Arbitrage and Algorithmic Trading: Overview and Applications. UNED. Available at: http://e-spacio.uned.es/fez/eserv.php?pid=tesisuned:CiencEcoEmp-Mnoguer&dsID=Documento.pdf [Acessed May 7, 2011]
Aumann, Robert J. (1987), Game Theory, The New Palgrave: A Dictionary of Economics, 2, pp. 460–482
Bergan, P. and Devine, C. (2005, Spring). Algorithmic Trading: What Should You Be Doing? Institutional Investor Journals. 1, pp. 14-18.
Butler, G. (2007). Liquidity Aggregation: What Institutional Investors Need to Know. Investment Technology Group, pp. 1-12. Web.
Chaudhuri, K. (2004, November). Mean Reversion in Stock Prices: Evidence from Emerging Markets. Managerial Finance. 30(1), pp. 22-36.
Chiu, J, Lukman D. W., Modarresi K., Velayutham A. S. (2011). High-Frequency Trading. Standford University. pp. 1-18.
Fama, E. F. (1970). Efficient Capital Markets: A Review of Theory and Empirical Work. Journal of Finance. 25(2), pp. 383-417.
Gatev, E., Goetzmann W. N., and Rouwenhorst. (2006, February) Pairs Trading: Performance of a Relative-Value Arbitrage Rule. The Review of Financial Studies. 19(3), pp. 797-827.
Hallahan, T., Vikash R., Moosa, I., Yacoub, A., O’Neil, B., and Backulja, M. (2009).Tournament Behavior in Malaysian Managed Funds: A Non-Parametric Analysis. Research at Business. pp. 1-37.
Hendershott, T., Jones, C. M., and Menkveld, A. J. (2011, February). Does Algorithmic Trading Improve Liquidity? Journal of Finance. 66(1), pp. 1-33.
Khandani, A, and Lo, A. (2007). What Happened to the Quants in August 2007? Web.
Lo, A. (2005). Reconciling Efficient Markets with Behavioral Sciences: The Adaptive Markets Hypothesis. Journal of Investment Consulting. pp. 1-44.
Lo. A. (2004, August). The Adaptive Markets Hypothesis: Market Efficiency from and Evolutionary Perspective. pp. 1-33. Web.
Malkiel, B. C. (2003). The Efficient Market Hypothesis and Its Critics. Princeton University. Working Paper # 91. Available at: http://www.princeton.edu/~ceps/workingpapers/91malkiel.pdf [Acessed May 7, 2011]
Wilson, G., and Banzhaf, W. (2010). Algorithmic Trading with Development and Linear Genetic Programming. Genetic and Evolutionary Computation. pp. 119-134.