Introduction
Gold prices are punctuated by ups and down patterns. For example, in the recent past, a positive trend in prices has been recorded compared to last century prices. This has attracted many both old and new institutional buyers, fund managers, high-end families, developing states to industrialized economies, and individual categories of investors to this security market. Much of this increase has been attributed to the dismal performance of alternative asset classes like equities, cash, house prices, and bonds, high inflation which has stabilized at double-digit figures in most developed economies, the panic of the economic and financial eurozone crisis, need to protect wealth from inflation effects and positive expectations of a massive investment return (Denver Gold Group 2010; Andrew & Mosayeb 2006).
Since 2004, gold has been advocated for as the main investment palace by many scholars which forced many European central banks to limit their sales for five years consecutively thus greatly impacting its price-setting and trends. The annual sale was limited to 500 tons with their cumulative gold sales of 2500 tons documented which added to the importunate low prices forced many closed mines resulting in shortages. Therefore, from the start of 2007, a new investment avenue- Xetra Gold was launched by Deutsche gold Börse to bridge this shortage and maintain trading patterns (Nadeshda & Thomas n.d).
This investment avenue was advantageous as it could be handled like normal security thereby leading to considerable benefits in comparison to the physical gold or gold futures investment options. Nevertheless, these man-made shortages resulted in higher prices and greater sales for investors. Much of these sales were motivated mainly by the need to reduce overreliance on a few foreign currencies, enhance alternative diversification strategies, confine growth in sizeable reserves, restorative of reserve composition, and finally to preserve national wealth and promotion of financial stability.
By the end of the 2011 season, there was an incremental gold demand which stabilized at 4067.1 tons with an estimated value of US $ 205.5 billion, the highest recorded in gold history. The growth was stimulated mainly by investment, jewelry and technology, and industrial sectors (World Gold Council 2010; 2011; Gold Bars Worldwide 2011).
Gold investment Vehicles
First, is the gold bullion which is considered cheap and is the most attractive investment options to invest in gold. Bullion is available in a range of sizes from one ounce to 400-ounce bar. The price attached to any depends on the fitness and weight embedded on the face of the bar. In addition, it is considered tax-exempt, liquid, and has international acceptance. However, billions attract storage charges and have no attached cash flows like interests and dividends.
Second is the gold coin like numismatic and bullion coins which are ideal for any investment purpose. Most of these investors are required to purchase as low as one ounce while others demand a minimum of five ounces. However, they offer different certificates for the same, charging a commission of between 0.25-3 percent with some deals completed through phones while others offer certified cheques.
The third is investing in gold stocks which are similar to any other stocks. It may be shared in future mines or existing mines. Generally, investors should observe the dividend payout history of the company, management competencies, company earnings record, price earning ratio, and current ratio before deciding on any purchase. However, on purchasing the existing mine shares more information like the mine’s political environment, production costs, and expected reserve should be critically observed.
Fourth is the gold options and futures which allow investors to earn profits when prices are falling or easily predict prices and trends. Under the contract method, most brokerage houses need as low as five percent of the total unit price thus making it more flexible to investors. Therefore investors can purchase a large amount of gold at a small cash price thus improving its earning potential. Finally is the investment in the jewelry market. However, most jewelry contains less than 24 karat gold thus making it a less attractive investment destination to gold-conscious investors (Peter 2010).
World demand and Price trends
World demand
The annual world gold demand has recorded a steady increase of nearly 11% to reconcile at an estimated 4000 tons in 2010. Most of this demand arises from India and China which account for over 55% of jewelry and 52% of investment demand. Specifically, India recorded a massive 38 percent increase in consumer demand for gold although the prices were up by almost 25 percent annually. This demand is attributed to the cultural link with metals. Imports of yellow metals within the country were expected to increase by 34.9 percent and exceed a record high of 1000 tons by the close of the year 2011.
In China, the recent strengthening of economic conditions and increasing maturity of its markets might depict positive implications for a steadier price increase in gold prices. The increased world demand for gold may be attributed to sturdy central banks buying behavior, increasing mine production, and finally the recommencement of producer equivocation as a small supply source (World Gold Council 2010; 2011).
Comparison of Gold trends for China and India: World Gold Council 2011
Price trends
Gold prices are influenced by market supply and demand patterns. The actual demand and supply should not vary according to central banks gold purchases and sales and supply of gold scrap but purely on market demand and supply. Gold investments are considered as a means of reducing portfolio volatility as the activities causing collapse of stock prices also tend to raise the price of gold. The demand of gold for investment is influenced by exchange rate expectations of a dollar, real interest rate, inflationary expectations, return on alternative assets, political turmoil situation in mining countries and lack of correlation with other assets.
Gold performance (2010) in developed markets
Gold performance (2010) in developed markets; World Gold Council 2010.
The world price of gold was on the increase within all major currencies of the world and specifically in the European markets where severity measures aimed at reducing financial crisis resulted in poor economic outlook and negative effect on local currencies. Most currencies slipped against US dollar and witness nigh volatility. In Euros (figure above), the gold prices increased by almost 23.1 percent sterling pounds while Swiss Franc increased by 14.3 percent. However, Canadian and Australian dollars fared moderately well and thus the prices of gold increased by 20.9 and 16.6 respectively.
Price trends of Gold from 2009 – quarter one 2011
Price trends of gold from 2009- 2011: Philip 2011
Gold price trends have witnessed an improvement in prices from 972.35 in 2009 to its highest of 1386.27 by the start of 2011 (figure above). However, the inter year deviation has also recorded a steady price increase. Much of this massive deviation in prices happens during financial crisis witnessed in most developed countries.
Gold prices forecast and direction prediction
The medium and long term future of gold continues to record an encouraging trend although long term disruptions exist. Most organizations are of the opinion that gold prices will hit the highest of US $ 2,000 mark. This prediction are based on high demand expectations from China and India, improvement in macro economic conditions- inflation and interest rates, improvement of US market and increasing pace of emerging economies interest in gold investment.
Prospects of gold as investment
The prices of gold have since increased by an estimated 180% within the past 4 years. Since January 2011, it has increased by almost 23% outperforming all asset classes in the US market. Therefore, gold has gained limelight as investment asset of choice attributed to its size, liquidity, size and depth and especially during this time of economic crisis and uncertainty experienced in most developed countries.
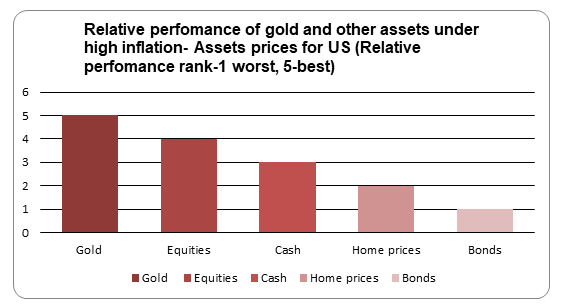
From the table above, Gold investment outperforms all assets in the USA market for the period 2011-2015. It is important to note that house prices received some support but as the recession continued, this stopped. Cash recorded a dismal performance due to monetary policies while bonds’ poor performance was attributed to high inflation rates steepening the yield curve and delayed tightening of monetary policies. It is important to note that the most favorable allocation of investors’ finance to a given set of asset classes depends on the variability of his risk tolerance. Investors who are risk lovers can allocate more money to risky businesses like equities. The risk-averse investors concentrate mainly on bonds and cash items.
Investment trends
Under exchange-traded funds and within the second quarter of 2010, through exchange-traded funds, a total of 273.8 million tons fresh gold purchases were recorded. This was the second-highest quarterly record in gold investment history. Therefore the total gold holding stood at 2041.8 tons values at US dollar 81.6 billion. During the same period, gold shares made tremendous improvements all over the world. For instance, in the European market, gold trade funds increased their holdings by 70 tons, and the Australian stock market recorded a decline of 0.5 tons (World Gold Council 2010; 2011).
Secondly, GLD options also witnessed an increase of 15.3 percent to stabilize at 13.3 million contracts.
Although this represented a massive improvement from quarter one figures of 11.5 million, it was way below the quarter four 2009 figures of 13.7 million. Much of the trading was between May and June due to the highest prices recorded but the latter slowed afterward.
The main challenge to investors was the volatility in gold prices which reduced their investment appetite. Specifically, during the quarter one period, the volatility increased by almost 5 percent to stabilize at a 23.6 percent level (World Gold Council 2010; 2011).
Finally, the counter market was an important transaction source mainly during April to June period. However, this market is mainly active during May and June and most investors resort to methods like diversification, wealth preservation, and protection against tail risk to increase their portions.
Factors influencing gold prices trends
First, is the poor future forecasting due to the frequent low prices of gold. This has resulted in limited sales and many mining firms were forced to close their mines as a result of frequent losses. However, as the demand increased, many firms could not meet their supply requirements due to limited underground resources and supply lags and so prices increased considerately. Second is the increased demand and popularity of gold from new market niches in the jewelry and technology industry and as an investment asset. This demand is attributed to its consideration as a safe investment haven, prevaricate against inflation, unstable stock markets, it is not attached to government finances, and finally the negative correlation with other asset classes.
Nevertheless, investment contributes to a massive portion with almost 15 percent of world total gold production is held in physical form by investors to provide a natural hedge against the weak currency. The third reason is the steady escalating transportation and energy prices which have made gold procurement very expensive. In addition, gold mines are under strict environmental regulation which has since increased the exploration costs thus price hikes (Andrew & Mosayeb 2006). Fourth, the political instability in main mining countries of Africa, Asia, and Latin America has contributed to gold market shocks. Moreover, the problem of mine ownership rights within major world producers like Russia have increased supply shocks in the gold market thereby contributing to an increase of the gold price volatility.
Finally, the loss of major currencies’ purchasing power added to the additional supply of currencies due to cheap policies adopted by developed countries during the financial crisis to boost economic growth. The falling of the US dollar which is the base currency for gold prices resulted in cheaper gold for other currencies which resulted in more purchases. With the prospects of further weakening of the dollar, more increased prices are expected.
Gold annual investment return
Gold has witnessed a massive return to investors within the last 4 years despite unpredictable price variations. This strong demand has been considered a haven for investors who are keen on excellent returns.
Percentage return gold (log returns): Madan & Kavita October 2011.
Comparison of portfolio return with other asset classes
Investors consider gold as an indemnity for financial assets which has the potential for increasing risk adjusted returns of any assortment. In this perspective, gold has acted as a risk management and portfolio diversification device in the wake of financial soundness. In comparison to other assets, the return from gold investment has witnessed a tremendous return to investors (figure below).
Percentage returns: 2006-2011; Madan & Kavita October 2011.
From this table gold offered almost two times what other investment portfolio offers and thus has been advocated for by most investment managers.
The future of gold demand
Under the technology and industrial application sector, gold forms a major ingredient in the manufacturing of semiconductors and dental items due to its helpful material purpose. In the quarter one 2010, the demand in this sector from the main electronics increased to 103.2 tons representing 31 percent increase. Specifically, the electronics sector rose by 40 percent to reconcile at 69.9 tons. This was attributed to increased consumer spending after the recession.
In this sector, Japan contributed almost 60 percent while the USA had 50 percent. However, the future of gold for this purpose is under intense pressure to economic recession, policy, and export regulations which have resulted in low demand from major destinations like India and China. A decline in demand for gold in dentistry and other related functions was noted. During the 2011 period, the semiconductor market recorded almost the highest sales levels which were supported by electronics demand.
In the jewelry market, the global market demand has recorded a steady demand for almost five quarters. Globally there was a 15 percent decline valued at the US $ 25.9 billion. Nevertheless, in 2011 demand of 1962.3 billion was 3 percent lowest compared to 2010 figures due to the economic meltdown recorded. Almost this market is shared between India and China which contribute almost 1/3 of the world’s jewelry demand. In India, the demand stood rose by 291 percent to reach the highest of 147.5 tons; Vietnam (+20 percent); Saudi Arabia (+25 percent); United Arabs Emirates (+29 percent), and Hong Kong (23 percent). Therefore, should prices increase to an unforeseeable future coupled with a decline in the US economy, then more difficulty might be experienced (World Gold Council 2010).
There is evidence of investment slowing down as a result of the economic meltdown. Therefore demand has not reached its full potential status. The 2011 demand was attributed to a mixture of liquidity variables, speculation, and its function as a store of value.
Conclusion
The steady rise in gold prices in the recent past has been a result of banks’ low-interest rates, weak dollar, central banks policies, and financial stress experienced in many developed countries. These factors have increased gold prices, however, due to the stabilization policies witnessed in the recent past, it can be true to conclude that a slight price drop might be expected shortly. Contradictorily, numerous forecasts for the current period 2012 in addition to the historical trends, give an opposing view of price increases for more time to come. This is because it might take a longer time to stabilize macro-economic challenges that resulted in such price increases.
A second important observation is that given the interlinkages between the uncertainties affecting world prices; it is hard to predict a specific date when all these conditions will be stabilized. For instance, the euro-zone debt dilemma could have a huge financial strain that might outweigh the 2008-2009 catastrophes. This again could hasten serious investors’ reevaluation of the future and nature of government securities being considered now as safe and profitable investment opportunities.
Moreover, the expansion of most central banks’ balance sheets in purchasing more gold has a negative implication on the inflation levels. It increases the prices of products, but, the inflationary pressures are assumed to have been well contained. It is important to note that the huge liquidity injections to the banking sector during the crisis period have had a spillover effect into the economy and asset prices are experiencing steady increases thus more inflationary pressures.
The third conclusion is the political instability in North Africa and the Middle East could result in increased gold prices by affecting major market destinations like China, India, and Japan. This political turmoil increases oil prices which translates into high prices of goods and services thus creating inflation.
Fourth, is the weakening of the US dollar against world major currencies thereby affecting short-term gold prices. The loss of currency value results in low investors’ confidence in the currency which calls for an alternative investment portfolio resulting in high gold prices. Therefore the potential role of gold as an insurance against unstable economies is clear. Therefore we can confidently conclude that the financial crisis has led individuals to believe that gold is a safer investment avenue than the Swiss franc.
References
Andrew, CW & Mosayeb, P 2006, ‘Gold investment as an inflationary hedge: Cointegration evidence with allowance for endogenous structural breaks’. Web.
Denver Gold Group 2010, ‘Investing in Gold’. Web.
Gold Bars Worldwide 2011, ‘Diverse range of Gold investment bars’. Web.
Madan, S & Kavita, C 2011, ‘Prospects of Gold as an investment special report’. Web.
Nadeshda, DM & Thomas H n.d., ‘Gold in the investment portfolio’, Frankfurt school working paper no. 87. Web.
Oxford Economics Report 2011, ‘The impact of inflation and deflation on the case of gold’. Web.
Peter, B 2010, ‘Investment in Gold’. Web.
Philip, K 2011, ‘Gold survey 2011’. Web.
World Gold Council 2011, ‘Gold demand trends’. Web.
World Gold Council 2010, ‘Gold investment quarterly digest’. Web.