Background
Governments cannot stabilize their economies if they do not work with financial institutions and investors to establish a lasting solution to inflation and other economic challenges. The purpose of involving all economic stakeholders in discussions regarding development is to establish policies that will create a healthy business environment for all players and consider the rights and needs of consumers. Some governments borrow money to finance their projects and recurring expenses, and this means that they expose themselves to bad debts (Coyle, 2010). Central banks and other key financial institutions should always be ready to take drastic measures to cushion their governments from unreasonable borrowing and spending. Governments collect taxes and use the money to finance their projects and expenses. The central banks play a significant role in ensuring there is a reasonable supply of money in the economy to avoid inflation. Therefore, central banks should work together with governments to cushion their economies from inflation and other economic challenges. This essay uses the IS-LM model to examine the impacts of cutting on expenses, increasing taxes, and liquidity of the banking sector to reduce budget deficits.
The IS-LM Model
This model was developed by John Hicks and Alvin Hansen in 1937. It explains the interaction between interest rates and output. The initials stand for investment and savings while LM means liquidity preference and the money supply. Therefore, this model explains the relationship between investments and savings and how this affects the liquidity preference and the availability of money in the economy. The chances of stabilizing an economy are high when the equilibrium brings a balance amongst all the factors in the economy. In addition, it explains the movement of the aggregate demand curve and shows the stability of the economy when different stabilization policies are established.
Application of the IS-LM Model to Reduce Budget Deficits
A budget deficit is a situation where the government is forced to spend more money than what was allocated to various projects. This means that a budget becomes contained and is unable to meet its targets because it does not have money to sustain and finance its projects (Goolsbee, Levitt, and Syverson, 2013). Borrowing loans from international financial institutions and grants from donors is a viable solution that governments may use to solve this problem. However, these solutions are not always available whenever they are required, and this means that they are unreliable. Moreover, politics has a significant impact on the success of these approaches to stabilize an economy and reduce the budget deficit (Harford, 2006). Therefore, internal mechanisms like reducing government spending and increasing taxes are more effective in managing budget deficits. Moreover, the central bank can increase the liquidity of the banking sector by releasing more funds and advising commercial banks to lower their interest rates.
An increase in taxation means that the government will collect more money from the public. Taxation is a government policy where citizens and corporations pay money as tax to enable the government to offer public services. The government uses different approaches to determine the amount that citizens and corporate pay. Taxes may be paid directly through a deduction of some percentage of an individual’s earnings and requiring the registration of businesses or indirectly by increasing the prices of goods and services (Levitt and Dubner, 2005). The money raised is used to finance various projects and ensure public services are offered without hitches. This is an effective and long-term solution that enables governments to manage budget deficits. It discourages investors because they have to pay high taxes to start their businesses, and this may affect their profit margins (Coyle, 2010). Moreover, it exposes the public to heavy spending on basic needs and constrains the economy, and limits investment levels. High taxation means that investors will spend a lot of money to establish their businesses, and this discourages development.
Cutting on expenses is a quick-fix solution to the budget deficit, but this practice may be applied to ensure governments live within their means. Most public resources are wasted by irresponsible servants. Issues like corruption and negligence expose governments to unnecessary spending, and this means that there will be few development projects (Harford, 2006). Some governments spend a lot of money on unnecessary activities like foreign trips, parties, and expensive lifestyles. These activities do not generate income; therefore, they waste resources and force governments to look for money to finance their development projects and meet the recurrent expenses (Levitt and Dubner, 2005). A reduction of government expenses is a sure way of reducing the budget deficit.
Lastly, the central bank may help a government to reduce a budget deficit by increasing the liquidity of the banking sector and undertaking expansionary open market operations. Central banks have fiscal policies that control the lending of money to the public, and this determines the amount of cash in circulation (Levitt and Dubner, 2005). These operations attract investors to borrow money and invest in various projects. Governments can issue tenders to private investors, and this means they will not have to finance their projects until when they are completed. The banking sector may establish friendly policies like low-interest rates, long repayment periods, and attractive earnings on fixed deposits to attract investors (Goolsbee, Levitt, and Syverson, 2013). These practices encourage the public to borrow and invest in income-generating projects. Therefore, the gross domestic product (GDP) of a country increases because there is a high rate of income generation. The money in the public’s hand is supposed to circulate as many times as possible to ensure it generates more income (Frank, 2008).
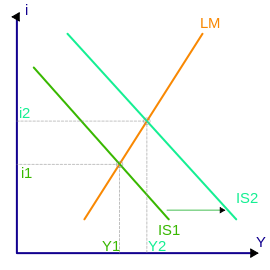
When the IS curve moves to the right, it raises the equilibrium interest rate and national income to achieve an aggregate demand. Therefore, the government will collect more money from the public and corporate to reduce its budget deficit. In addition, the trend will cause an increase in liquidity and expansion of open market operations (Levitt and Dubner, 2005). Therefore, it becomes easier to obtain bank loans and invest in income-generating projects. However, this may limit the long-term growth of the supply side because it causes discourages private investments.
The second figure shows that there will be an increase in exogenous investments and consumer and export spending. People will spend less on imports and this means that money will circulate within the country’s economy, and more will be generated through exports (Frank, 2008). Sometimes, the LM curve moves downward and to the right, if the central bank initiates open market operations and increases liquidity, and the government collects more money through taxation. This act lowers the interest rates and raises the equilibrium national income because more people will generate wealth through investing in business activities. Moreover, the move causes a change in the liquidity preference that shifts the LM curve downwards causing an increase in income and a decrease in interest rates.
References
Coyle, D 2010, The Soulful Science: What Economists Really Do and Why It Matters, Princeton University Press, New Jersey.
Frank, R 2008, The Economic Naturalist: Why Economics Explains Almost Everything, Virgin Books, New York.
Goolsbee, A, Levitt, S and Syverson, C 2013, Microeconomics, Worth/Macmillan, New York.
Harford, T 2006, The Undercover Economist, Oxford University Press, Oxford.
Levitt, S, and Dubner, S 2005, Freakonomics: A Rogue Economist Explores the Hidden Side of Everything, Allen Lane, London.