Introduction
In this laboratory work, a weight was suspended from a spring fixed in a holder. The purpose of the work was to find out the effect of the mass of the suspended weight on the displacement. In fact, the mass of the weight affects the force of gravity experienced by the objects and affects the spring: the stronger this mass is, the more extension of the spring should be expected. For this reason, it was more interesting to investigate the relationship between the force applied to the spring (gravity) and the displacement (stretch) of that spring.
Data And Analysis
The weights of five different weights (including zero control) for three different springs were obtained as direct measurements. The difference between the springs was due to their coefficients of deformation: that is, the springs differed in strength and tensile strength from each other. Information about the direct measurements is presented in Table 1. At first glance, it can be seen that the higher the mass, the stronger the elongation for all three springs.
Table 1: Data from direct measurements
In fact, the greatest interest was not the mass but the force of gravity, which affected the springs. As it is known, the force of gravity is defined by the formula F = mg, which means that with a known mass, it is not difficult to determine the specific force of gravity for each of the tests. This data is included in Table 2, which relates the values of the mass of the weight to the values of gravity for these objects. A value of 9.807 m s-2 was taken as the acceleration of free fall, which is a reference value (Clark, 2022).
Table 2: Conversion of mass (in kg) to gravity (in N)
Thus, having data on the values of the applied force for each of the five tests and the vertical displacement of the three springs, it becomes possible to visualize this information: it is shown in Fig. 1. As should be noted, this dependence was linear for all three springs, which is reflected in the high values of the coefficients of determination. The slope of each regression line shows how much the value of vertical displacement changes when the force index increases by one Newton. Thus, for spring #2, this rate was the maximum, and for spring #3, the displacement was the minimum as the applied force increased. Since F= -k∆x, the slopes of these lines are equal to -1/k, which is the inverse of the negative stiffness coefficient, in other words, the stiffness of the second spring was minimal, and the stiffness of the third spring was maximal, which is why the third spring had the smallest displacement.
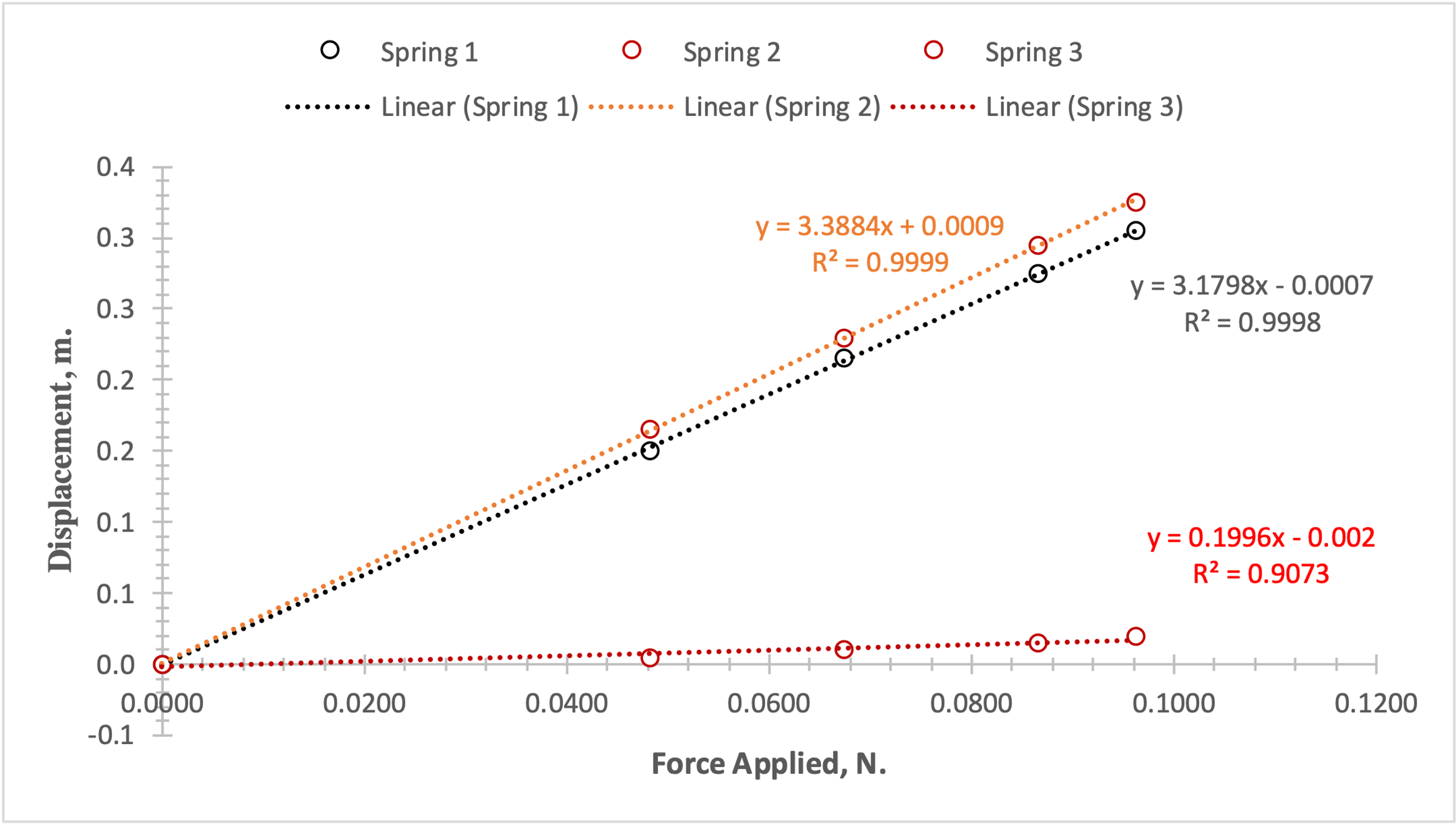
Conclusion
The purpose of this laboratory work was to demonstrate the relationship between the vertical displacement of the spring and the value of the force applied to it. The force chosen was the force of gravity, which varied as a function of the mass of the weight attached to the spring. It was shown that these dependencies were linear upward trends. To put it another way, an increase in the applied force increased the vertical displacement of the spring. This seems logical since the greater the mass applied to the spring, the more it stretches. The rate of this growth was different for each of the three springs. The reason for these differences was the coefficient of stiffness corresponding to the force of extension of the spring when a force was applied to it. It was shown that the third spring had the maximum value of this coefficient, and therefore the spring exhibited the lowest tensile strength. All of this together leads to the conclusion of the overall success of this laboratory work and confirmation of the theoretical concepts.
Reference
Clark, V. (2022). What is standard gravity? Wisegeek. Web.