Management Science- Management Science is a structured approach to problem-solving. A structure is an algorithm or steps on how to solve a problem. The approach means to understand (defined) a problem. Problem-solving means to make a decision. To make a good decision, the person has to write the problem down in a mathematical model. Then, he/she has to decide and come out with a solution (best solution). Finally, the person has to think about it if the solution is effective or not. If it not effective, change it.
Mathematical Model- These are models, which use mathematical concepts to analyze situations for decision-making. They can take many forms, from statistical models to equations models. Mostly they are important for computer applications. They can describe the behavior of a system, which can be used by businesses for decision-making. They have a number of variables, which are used, and they include random variables, output variables, input variables, decision variables, state variables. An example of these models includes a linear programming model.
Deterministic and stochastic (probabilistic) models- Deterministic model is that model where there are no random figures used in predicting the future. The model produces similar output regardless of the time used so long as the variable input used is the same. They include chemical reactions in chemistry.
Stochastic are those models that employ probability distributions as inputs, it has random numbers or variables which allow outputs to be variety. The inputs are based on observations. Once the observation has been, made data is collected and given the theoretical probability, which is used in solving the real-life process.
Linear Programming- It is a mathematical model, which uses algorithms to solve a certain problem. It involves techniques consisting of sequence steps to arrive at an optimum solution. The linear programming model has four components, which include objective function, constraints that provide limitations for restricting the alternatives available to decision-makers. Decision variables, which represent choices available to the decision-maker in terms of amounts of either inputs or outputs, and parameters. The objective function can be either to maximize or to minimize a certain decision variable, so; it is an expression, which is used to determine the total profit. It consists of a mathematical statement of the objective and a mathematical statement of each constraint. These statements consist of symbols that represent the decision variables and numerical values called parameters the parameters are fixed values ; so the model is solved given those values.
Structure of a Linear Program- A linear programming problem has a certain structure including a linear function a decision variable, objective function, constraints and optimum solution. At first objective function is developed which enables the decision variables and constraints to be constructively decided. What follows is a feasible solution where a number of solutions are expected to emerge; this is where an optimum solution is obtained. An example of a linear programming model is shown below.
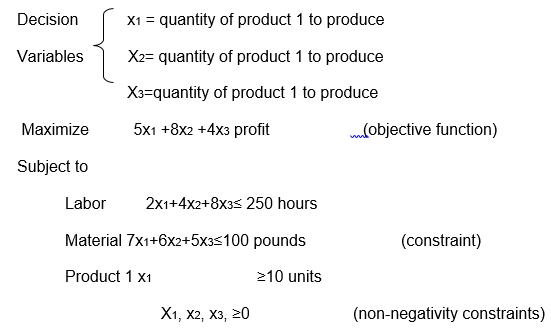
Binding constraint is a constraint that forms the optimal corner point of the feasible solution space, which limits the value of the objective function. It affects a decision because after an optimum decision has been arrived there is no surplus left. Its variables cannot be altered because it is restrictive either it is not available in abundance or it is the only resource that is available in the market.
slack occurs in a ≤ constraint when the left side is less than the right side, if the optimal values of the decision variables are substituted into the left side of a binding constraint, the resulting value will be exactly equal the right – hand value of the constraint.
Sensitivity Analysis provides a ranges of probability over which the choice of alternatives would remain the same. which can be useful for the decision maker to have some indication of how sensitive the choice of an alternative is to changes in one or more of these values.
Shadow Price which is a marginal value that indicates the amount by which the value of the objective function would change if there were a one- unit change in the RHS value of that constraint. if the constraint is non- binding , its shadow price is zero, meaning that increasing or decreasing its RHS value by one unit will have no impact on the value of the objective function. Nonbinding constraint have either slack (if the constraint is ≤ or surplus (if the constraint is ≥).
Dual Problem it is the reformulation of the original constraints to form a new problem, which contains algorithms, which can be solved by the computer. In a situation of dual problem, we have variables domains and constraints. In each variable of a dual problem, it has an element of original constraint. It is used when changing the optimum solution; it shows what effects a change in a variable will have to a decision or the optimum decision. A dual price describes the unit worthy of any resource it gives the rate of improvement of the optimum solution. It does not specify the amount by which a resource can be increased while maintaining the same rate of improvement. Logically, in most situations we could expect an upper limit beyond which any increase of the resource would make its constraints redundant , with the result that a new basic solution and hence, new shadow prices, must be sought. The presentation below addresses the point of determining the maximum change in the availability of a resource before its constraints becomes redundant.


