Modeling is crucial in economics because it is used in place of the real experiments that could be expensive, time consuming, and dangerous. Mathematical models describe situations with a few words using tools and theorems for making general statements. Here, the focus is on how to explicitly state assumptions with a clear and precise ease of making multi dimensionality descriptions.
In economics different mathematical models have been developed to address certain market trends and behaviors such as demand and supply with time. One such is the models related to competitive markets. The product demand and supply and price changes are dynamic aspects of the system and can be modeled through a differential equation with a constant solution referred to as the equilibrium of the equation. Here,
x(t) = f (x) (equilibrium equation)- definition
Based on the above definition, the linear differential equation can be expressed as:
x + u (t) = w (t)
In this case, w (t) and u (t) are functions of t in the above expression. The homogeneous case here is u (t) =a and w (t) =0 giving the solution for the differential expression:
x + ax =0 as x (t) =Ae-at. In this case A is taken as an arbitrary constant. The case for a non-homogeneous situation is x + ax = b where b≠0 and a =0,as solution is x (t) =bt +A providing a solution with known initial state x(0) as given by:
x (t) = e-at +b/a
A typical example is the demand and supply mentioned in the above scenario. The dynamics of a price of a single commodity is considered. The demand and supply function is stated as below:
Qd=a1-b1P,
Qs=a2-b2P, both satisfy the condition aj, bj>0.
In the above expressions, Qd and Qs are respective values for the demand and supply for the given price P within the parameters aj and bj. If the price changes are taken with the changes in time t, excess demand proportional to the time t is Qd– Qs expressed as
P (t) =m (((Qd (t) – Qs (t))), where m>0
When substituted: P (t) + m (b1+b2) P = m (a1+a2) giving the solution shown here:
In this case
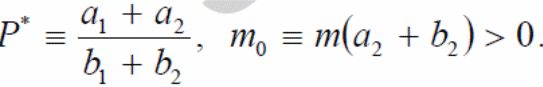
Satisfying the general case:
In this case, the problem related to the above model is demand and supply of a product and its effect on price with time illustrated as x (t) = f (x).