Introduction
An important element of learning is to connect mathematical concepts with physical concepts. Graphical representations of mathematical functions allow one to visualize the meaning and power of mathematical equations. The power of computer programs and graphing calculators provide a thorough connection between algebraic equations and visual representation, fostering a heightened appreciation and understanding of mathematical language (Pierce, 2010, p. 1).
Solution to the given problem
- The x-intercept and y-intercept are determined algebraically, as shown below:
- y-intercept is the point where the line meets the y-axis, that is, the value of x at this point is 0. Therefore substituting for x in the equation y = – (2/3)x + 30,and solving algebraically yields y = 30. Hence the y-intercept is 30.
- x-intercept is the point where the line meets the x-axis, that is, the value of y at this point is 0. Therefore substituting for y in the equation y = – (2/3)x + 30, and solving algebraically, 0 = – (2/3)x +30; (2/3) x = 30; x = 45 therefore the x-intercept is 45
- In plotting the graph, the following coordinates where used.
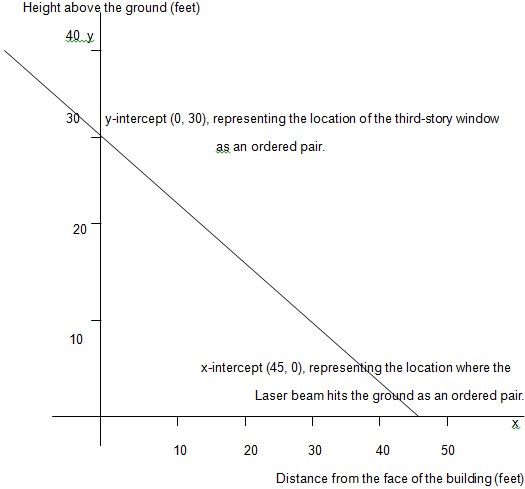
- Since the building is perpendicular to the ground, the laser beam, the building and the horizontal distance from the face of the building form a right angled triangle. Using Pythagoras theorem therefore, the height of the laser beam 30 feet away from the face of the building can be algebraically determined;
The cross sectional view of the right angled triangle is such that the height of the laser beam would be the hypotenuse, thus:
- y = – (2/3)x + 30
- y = – (2/3)30 + 30
y = 10 This is the height of the wall when the laser beam is 30 feet away from the face of the building.
Height of the laser beam = √ (102 + 302) = √ (100 + 900) = √ 1000
This is approximately 31.6 feet.
Therefore, the height of the laser beam 30 feet away from the face of the building is approximately 31.6 feet.
The determination of the height of the laser beam graphically follows from the measurement of the path traced by the laser beam from the y-intercept (representing the location of the window of the building) to the x-intercept (representing the point at which the laser beam hits the ground) in a accurately scaled graph.
5. The first quadrant is the only quadrant which is relevant to this situation. If such physical principles as reflection and refraction of the laser beam were stated in the original situation, then one would argue that quadrants one, two and four are relevant.
Based on the attributes of the story problem, the graph is a reasonable visual representation of the path taken by the laser beam, only on the condition that the extensions of the line graph beyond both the x and y-axis is overlooked.
Reference List
Pierce, R. (2010). Algebra Menu. Math Is Fun.