An Overview of the History of Pythagoras Theorem
To date, Pythagoras theorem is arguably the sole primary theorem in all mathematical genres. Even though it has geometric origins, the theory generally ascribed to Pythagoras has been applied in almost all platforms of science disciplines. Numerous proofs have been developed in concurrence and affirmation of the original seminal Pythagorean theorems; some of these verifications were discovered by the most unpredictable persons in utter simplicity, including the twelve-year-old lad (Albert Einstein), an American president among others.
Although, currently we best know the theorem in its algebraic notation, a2 +b2 = c2 – where from we can determine magnitude of one side of a right angled triangle given the other two, Pythagoras visualized it with a geometric perspective in which he related the areas of the resultant squares generated by the sides of a right angled triangle. It was only the convenient tool of algebra, brought to the fore around 1600 CE that has bequeathed us with this simplified algebraic version of Pythagoras theorem (Maor, 2007, p. 22). The elementary components of the theory are believed to have been discovered and utilized by the ancient Babylonians, and probably the Chinese approximately 1000 years before Pythagoras proved the theorem in about 500 BC. Old Babylonian tablets dating back to roughly 1800 -1600 BC, were unearthed whose inscriptions upon close scrutiny revealed a list of Pythagorean triples (that is, positive integers a, b and c such that a2 + b2 = c2) for example (3, 4, 5) and (4800, 4601, 6649). A good example of these Babylonian tablets is the Plimpton 322 collection at Columbia University. The mechanism employed by the Babylonians to arrive at these large Pythagorean triples is yet to be established, though Euclid’s algorithmic analysis formulated 1,500 years later concretized the Babylonian findings. Euclid considered a set of two positive integers, say u and v, where u > v; and did show that the three Pythagorean triples a, b and c can be deduced as;
a = 2uv, b = u2 – v2 and c = u2 + v2
It follows then that;
a2 + b2 = (2uv)2 + (u2 – v2)2
=4u2v2 + u4 – 2u2v2 + v4
=u4 + 2u2v2 + v4
= (u2 + v2)2
= c2
From which it is evident that the Pythagorean relation a2 + b2 = c2 is satisfied; and its converse still holds that if the sides of a triangle satisfy the equation a2 + b2 = c2, then the triangle is a right angled triangle (Morris, 1996, p. 1).
This reflects the fact that Babylonians did not only have the Pythagorean knowhow, but that they were also equipped with the requisite computational and number theory tools. Although many a people attribute the engineering design of the Egyptian distinguished monumental pyramids to the genius of Pythagoras concepts, a greater percentage of historical inquiries into Egyptian Mathematics do not find any foreknowledge of Pythagorean concepts in Egypt at the time (Greene, 2011, p. 1).
Pythagoras; the enigma of mathematics
Although little is known about him; for many historical works on him are speculations and mere fiction, it is believed that Pythagoras was born around 570 BC on the island of Samos. Greek proponents of the day were scholars in mathematics, astronomy, music and philosophy which proved to be a precursor to Mediterranean civilization. About 530 BC Pythagoras forsook Samos and found seclusion in Croton, a southern coast of the current Italy. Where he initiated a brotherhood – school, which was to be the vehicle of transmitting the seminal Pythagorean discoveries to later generations. One of the Pythagoras’ key initial discoveries was on acoustics, in which he found that the pitch of sound produced by a string instrument is indirectly proportional to the length of the string, provided that the strings were of the same cross-sectional area and derived from the same fabric. He expressed the resonating harmonics numerically, thus describing tone variations quantitatively. This wonderful discovery made him hold the premise that numerical ratios govern the laws of nature, hence still the universe. His group inquired about number patterns, sequences, series and their varied implication in the universe. They investigated about square, rectangular numbers to mention but a few (Huang, 2005, p. 1).
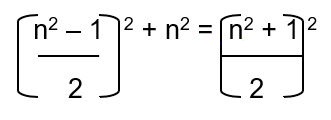
The initial approach employed by Pythagoras in proving this theorem has since been shrouded in mysteries, but many varied approaches were formulated later to confirm the validity of his proof. The same inquiry, while investigating about the relationship of the lengths of sides of an isosceles right angled triangle, Pythagoras discovered a unique and spectacular class of numbers which could not be expressed in ratio form. For instance, an isosceles right angled triangle of sides 1unit, 1unit would have a hypotenuse of √2 units which cannot be expressed as a ratio of two integers. This class of numbers, later given the title ‘irrational numbers,’ was to bring a new revolutionary dimension in mathematical analysis. History reports that Pythagoras died when he was almost eighty, and the circumstances surrounding his death are unclear, there being a political strive in the transition from the Babylonian reign to the Persian rain. We appreciate and celebrate his scholarly work, which has proved to be immutable in the study and exploration of mathematics as a discipline (O’Mearan, 1990, p. 252).
A brief illustration of Later proofs affirming Pythagoras Theorem
The Chinese Proof
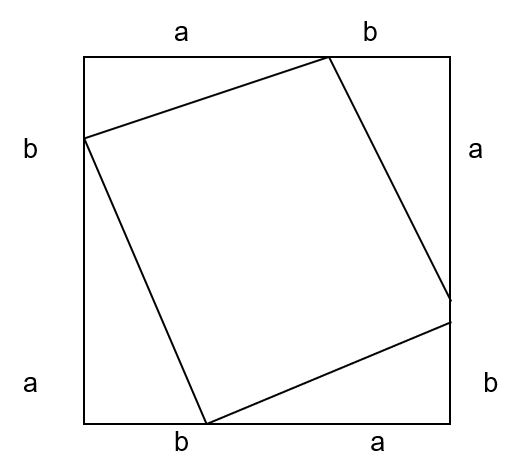
Let us assume that we have a perfect square of sides (a + b) units and an inscribed square of sides c units.
We can express the area of the interior square in two different ways;
Area of square = c2 square units. Or,
Area of square = area of the big square – area of the region not taken by the small
Square.
= (a + b)2 – ½ of4(ab)
= a2 + 2ab +b2 – 2ab
= a2 + b2 square units.
Therefore, since the two algebraic expressions represent the area of the same plain figure; they must be equal, c2 = a2 + b2, proving Pythagoras theorem (Khalaf, 1996, p. 1).
Proof using the area generated by the sides of a right-angled triangle
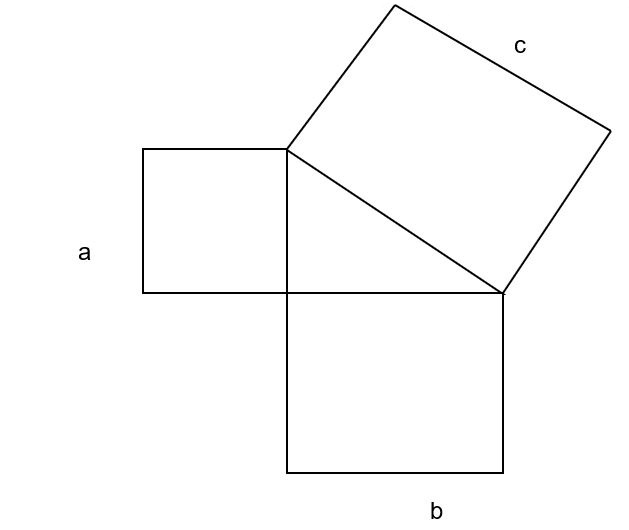
Assuming that the sides of the triangle can be produced to form perfect squares; then it can be noted that for any right angled triangle the area generated by the hypotenuse is the same as the sum of the areas generated by the two shorter sides. For instance, if a = 3 units, b = 4 units and c = 5 units.
Then, 52 = 32 + 42
25 = 25.
This can be ascertained by measurements of the length of the sides of the triangle and calculations of the areas of the resultant squares. If the relation does not hold, then, the triangle in question is not a right angled one (Allen, 1997, p. 1).
Proof using the concept of similarity
Consider a right angled triangle ABC
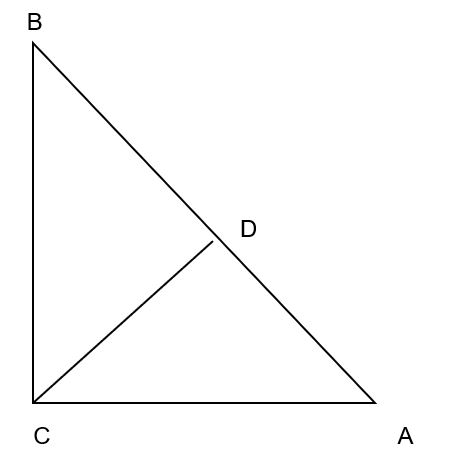
Let AB = c, BC =a, AC = b and AD = x, then DB = c –x
Assuming that line CD is a perpendicular bisector of line AB, then, the three triangles ABC, ACD and CBD are similar. This is due to the fact that all their corresponding angles are equal, and since they are similar, we expect the ratio of their corresponding sides to be equal.
BC/BA = BD/ BC
a/c = (c – b)/ a
a2 = c(c – x)
Also, AC/BA = AD/AC
b/c = x/c
b2 = cx.
Therefore, a2 = c2 –cx
a2 = c2 – b2
Proving the Pythagoras theorem that, c2 = a2 + b2
Epilogue
In retrospect, one cannot avoid to mention the diverse and varied areas of application in which Pythagoras theorem have served humanity through the ages. From the scientific arena of mathematics, physics, astronomy to the business world, literary field in which poems and songs have been sang in celebrating the beauty of this great milestone which triggered modern civilization (Sparks, 2008, p. 1).
Reference List
Allen, D. (1997). Pythagoras and Pythagoreans. Web.
Greene, N. (2011). Pythagoras of Samos Biography. Web.
Huang, R. (2005). Pythagoras’ Theorem in Chinese Mathematics Classroom. Web.
Khalaf, G. (1996). Pythagoras(569 BC – 475 BC). Web.
Maor, E. (2007). The Pythagorean Theorem: a 4,000-year history. Web.
Morris, S. (1996). The Pythagorean Theorem. Web.
O’Mearan, D. (1990). Pythagoras Revived: Mathematics and Philosophy in Late Antiquity. (1st ed). Oxford. Pg 252.
Sparks, J. (2008). The Pythagoras Theorem. Web.


