Introduction
Pythagoras Theory is a relatively simple theory used continuously in Standard Grade Mathematics and beyond. It is also used in Physics. It is used not only to simply solve the missing side of a right-angled triangle but also more extensively to solve Reasoning and Application problems and also can be used to solve many higher mathematics problems in trigonometry and in many topics throughout the mathematics syllabus. It is so basic that I’m sure anyone who studied it at school will remember it long after other theorems have been forgotten.
History
Early evidence of the theory can be traced back as far as 2000 BC with the ancient Egyptians. Pythagoras had traveled to Egypt and this may have influenced some of his beliefs. There is some evidence that they used a 3-4-5 triangle to form a perfect right angle. However, very little information pre-dates the Greeks so this remains a mystery along with many other ancient Egyptian stories. Hence the Theorem was credited to Pythagoras. What is more likely is that Pythagoras was the first to prove it. Pythagoras then generalized it to all right-angled triangles hence it is Pythagoras’ theorem.
Pythagoras was born on the island of Samos in around 582 B.C and died in around 500 BC He was a Greek philosopher and mathematician. He had been instructed in the teachings of the early Ionian philosophers Thales, Anaximander, and Anaximenes. It is believed that Pythagoras was driven out of Samos in 532 BC by Polycrates, the tyrant who ruled there. He moved to a Greek colony in southern Italy named Crotona where he set up a religious and philosophical school. A movement is known as Pythagoreanism.
Little is really known about Pythagoras’ actual work. His school practiced in secrecy thus making it difficult to distinguish between his work and that of his followers. Whether someone from the school or Pythagoras himself found the proof can’t be truly known. Hence the philosophy of Pythagoras is known through the work of his disciples. The school did make several contributions to mathematics. Pythagoras believed that all relations were based on number relations. He believed that numbers were the very essence of things and their motto was ‘all is number’. This was based on various observations in music, astronomy, and mathematics. They were interested in the principles of mathematics, the concept of number, triangles, and the abstract idea of proof.
Proof of Pythagoras Theorem
Pythagoreans carried out investigations into odd and even numbers and of prime and square numbers. They used this to back up their belief that whole numbers and their ratios could account for all geometrical proportions. By far the greatest and most well-known theorem is the hypotenuse theorem or Pythagoras’ theorem. It allows us to find the third side of a right-angled triangle given the other two sides. The formal definition is ‘the square of the hypotenuse of a right-angle triangle is equal to the sum of the square of the other two sides. It should be noted in Pythagoras’ terms he wouldn’t have meant square as the number multiplied by itself but as a geometrical square. The square on the smaller sides could be broke up and reassembled to make a square at the hypotenuse.
a² + b² = c²
¨ It only works for right-angled triangles
¨ We must have the lengths of two other sides
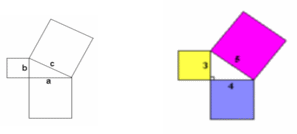
Here we can see that c is the hypotenuse and a and b are the other 2 sides.
Let a = 4, b = 3 and c =5, as shown above. The theorem claims that the area of the two smaller squares will be equal to the square of the larger one.
4² + 3² = 5²
16 + 9 = 25 as require
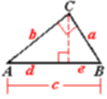
Draw a perpendicular from C to line AB.
- c/a = a/e; c/b = b/d
- ce = a2; cd = b2
- ce + cd = a2 + b2
- c(e + d) = a2 + b2
- c2 = a2 + b2
Pythagoras may have used the above methods but as his movement practiced in secrecy this is still the only estimation. Also, it cannot be fully understood if he himself or one of his disciples found this.
Euclid found the next method. Really it is not too different from the first method. Euclid’s method therefore only really supports the first proof. Euclid was first however to prove that the theorem was reversible. Therefore a²+ b² = c² can prove a triangle to be right-angled. He also generalizes Pythagoras’ theorem and proves that the area of a semi-circle along the hypotenuse of a right-angled triangle is equal to the sum of the areas of semi-circles on the other two sides. Euclid also used the following proof on his book II of elements:
”

A large square of side a+b is divided into two smaller squares of sides a and b respectively, and two equal rectangles with sides a and b; each of these two rectangles can be split into two equal right triangles by drawing the diagonal c. The four triangles can be arranged within another square of side a+b as shown in the figures.
The area of the square can be shown in two different ways:
- As the sum of the area of the two rectangles and the squares:
- As the sum of the areas of a square and the four triangles:
Now, setting the two right-hand-side expressions in these equations equal gives
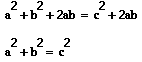
Therefore, the square on c is equal to the sum of the squares on a and b”. The following are a couple more proofs, which greatly improve the pupil’s understanding of Pythagoras. Even if they only understand one proof it is still worthwhile and increases their knowledge of Pythagoras.
The first proof involves a rectangle divided up into three triangles, each of which contains a right angle. This proof can be seen through the use of computer technology, or with something as simple as a 3×5 index card cut up into right triangles.
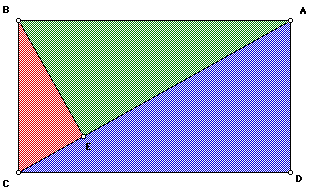
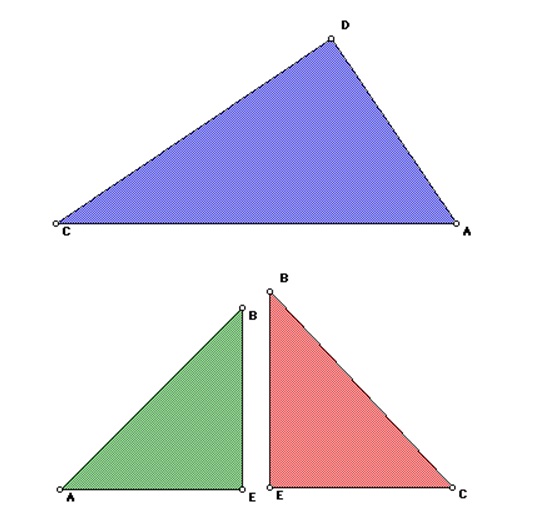
It can be seen that triangles 2 (in green) and 1 (in red) will completely overlap triangle 3 (in blue). Now, we can give proof of the Pythagorean Theorem using these same triangles.
Proof
Compare triangles 1 and 3.
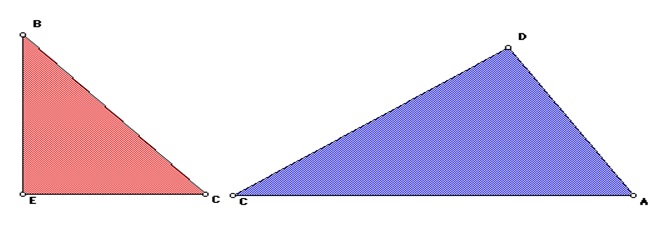
Angles E and D, respectively, are the right angles in these triangles. By comparing their similarities, we have
and from Figure 3, BC = AD. So,
By cross-multiplication, we get:
Compare triangles 2 and 3:
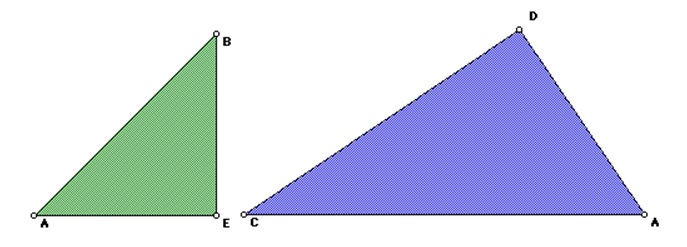
By comparing the similarities of triangles 2 and 3 we get:
From Figure 1, AB = CD. By substitution,
Cross-multiplication gives:
Finally, by adding equations 1 and 2, we get:
From triangle 3,
AC = AE + EC
So
The next proof of the Pythagorean Theorem that will be presented is one in which a trapezoid will be used.
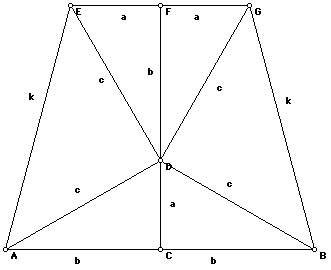
By the construction that was used to form this trapezoid, all 6 of the triangles contained in this trapezoid are right triangles. Thus,
Area of Trapezoid = The Sum of the areas of the 6 Triangles
And by using the respective formulas for area, we get:
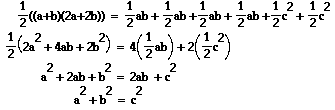
The proofs led to the Pythagorean problem, which is one of the earliest problems in the history of numbers. It was to find all the right-angled triangles that fitted the Pythagorean x² + y²= z². The three integers would be known as a Pythagorean Triple. E.g.
- 3, 4, 5.
- 5, 12, 13.
- 7, 24, 25, etc.
Conclusion
Today the Pythagorean theorem plays a significant part in many fields of mathematics. For example, it is the basics of Trigonometry, and in its arithmetic form, it unites Geometry and Algebra. Pythagoras’ Theorem is introduced to pupils in the middle of their high school career and becomes more important as they develop further in mathematics. Teaching the topic can be enhanced through computer technology and with proof so that the pupils can understand the concept behind the theory and not just the algebraic formula. This helps them see the importance rather than just substituting in numbers. This theorem and its proof were basic progress in the field of mathematics. It became a foundation of ancient geometry and had more control over theory and more practical appliances than any other. Today his theorem is used largely in building, architecture, carpenter, navigation, astronomy, and many other fields of work that involve mathematical calculations.
Each of these fields uses his theorem to try and choose either the hypotenuse or the two other sides in a right-angled triangle. Builders use Pythagoras’ theorem to calculate the magnitude of different aspects of their constructions. This allows them to work out the exact necessities of building resources needed. Architects use their theorem to work out a blueprint for the builders to use. His theory may be used to work out accurate lengths of roofs, also the structure of a house just to name a few. Carpenter uses his theorem to take the size of sides of their timber formation eg: corner fittings. Navigators and astronomers use his theorem to calculate distances between planets, satellites, and stars.
Works Cited
Maor, Eli, The Pythagorean Theorem: A 4,000-Year History. Princeton, New Jersey: Princeton University Press, 2007.


