Abstract
Computationally, when a population size phase exceeds the carrying limit, it becomes a super-martingale, and depletion occurs from a variation of martingale elements. Jagers and Zuyey (2020) explore such an extinction particularly among species with soft carrying capacity. They propose a model to explain this extinction with an initial non-random value of Z0 and the value of a nth variation by Cn, where n – 1, 2…. Thus, subsequent population sizes are denoted by Z1 = Z0 + C1 … indefinitely because of extinction. In this case, extinction is the final stage denoted as Zn = 0 implying that Zn _ 1 = 0 (Jagers & Zuyey, 2020).
No further finite absorbing levels of population sizes exist beyond this point. In an actual world, the time durations are of varying lengths hinging on an individual species’ life span, age range, and other superseding factors (Jagers & Zuyey, 2020). Species in settings with soft carrying capacities such as those with non-negative value K create a restricted expectation of a variation, given a full past history, is non-positive when the species surpasses the carrying volume.
Problem
Explaining population distinction is technical; thus, requiring a simplified model. Some of the population changes are homogenous and take place within unspecified periods. For others, such as those in soft carrying capacities, they die out when their carrying capacities are exceeded leading to extinction. However, the time durations cannot be estimated as they vary from species to species. As a result, these variations cause classification problems necessitating the development of a simplified framework.
Method Used
To avoid these technicalities, Jaggers and Juyev (2020) propose a model assuming that the variation Cn denotes a single individual dying (minus 1) with a restricted probability limited to 0. Changes occur after the death or birth of members of a species, denoted Cn, n ∈ N. N designates a set of positive values and C implies change. Each size variation is a valued random integer used in population description. When the population dies, no assumptions are made about the duration of changes that in actual life can vary as influenced by several internal and external factors.
New Results and Possible Extensions
The model is simple and unrestrictive; hence, evading uniformity constrains and is linked to irreducibility. In other words, the model implies that all populations in such environments will extinct or die. Mathematically, the framework complies with a supermatingale convergence characteristic and probability of attaining an absorbing extinction condition. Compared to other models, this framework augments an understanding of the carrying volume and extinction, a sigma-algebra for all activities, including nth. In contrast, other models only quantify eco-evolutionary processes linking population decline to the loss of genetic distinction. The model is Fn with a load capacity illustrated as K > 0, considered a large natural integer. As a carrying potential of the community implies that the conditional probability of the imminent transformation, considering its history, satisfies a number of assumptions (Jagers & Zuyey, 2020). The first argument maintains that, as previously elaborated, load capacity does not offer a normative restriction: population size may surpass it, but then will continue to decline for frameworks with holding abilities that are dependent on individuals as shown below.
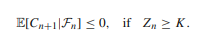
The super-martingale premise of the species size process is one fundamental tenet of the assessment; the other is that all members of a population, regardless of circumstances, often face a distinct chance of dying unknown to the other species. In particular, denoting by Z+ the range of non-negative integers (Jagers & Zuyey, 2020). Assumption two is a logical principle that can be simplified in many frameworks as shown below where € > 0 denotes as;
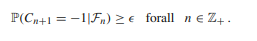
Its objective is to minimize snares when the system enters a subcategory of conditions that do not include zero and have no way out. Overall, based on the starting condition, the population either dies rapidly or expands beyond and around the holding ability K before it becomes extinct.
Reference
Jagers, P., & Zuyev, S. (2020). Populations in environments with a soft carrying capacity are eventually extinct. Journal of Mathematical Biology, 81(3), 845-851. Web.