Introducing students to an entirely new type of a mathematical problem requires assisting them in developing the necessary intuitive understanding of the subject matter and promoting the acquisition of the skills that will guide them toward applying the newly acquired abilities to solving specific problems (Goos et al., 2020). In the case under analysis, assisting students in acquiring the skills needed to embrace the concept of basic mathematical operations with positive and negative numbers can be implemented with the help of two key strategies. Specifically, the use of visual representations of the management of negative and positive numbers combined with the application of metaphors for representing the process of manipulating positive and negative integers, must be considered.
5 − (−3) = ?
In order to help students solve the specified problem, the teacher will have to help them embrace the concept of negative integers and their subtraction. The use of the number line could be seen as a possible solution to the problem at hand. Specifically, students will mark the minuend and the subtrahend on the scale. Afterward, the teacher will have to use two-color chip, each color representing either a positive change to a number or a negative one.
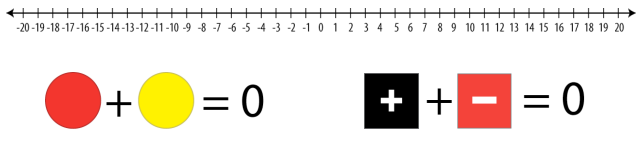
Afterward, the teacher will introduce the students to the logic behind moving the chips on the scale, with the shift to the right representing addition, whereas the transfer to the left representing subtraction. The specified concept will have to be practiced with positive numbers first. As soon as the learners recognize the logic behind the specified operation, the notion of negative integers will have to be introduced (Goos et al., 2020). Placing them on the scale, the teacher will explain that the directions are reversed in the specified scenario. Specifically, subtracting negative number will imply moving it to the right, namely, adding it.
Another approach to helping learners solve the described problem will require using the visual of a scale in order to represent the difference between positive and negative integers (see Fig. 2) (Goos et al., 2020). Specifically, the learners will be explained that, in case a zero is “heavier” than the integer, subtraction is replaced with addition, and vice versa.

6 ÷ 2 = ?
To explain the specified problem, a teacher may consider helping a student view division as the process of breaking a specific integer into several equal parts. In the case in point, the student will be provided with an explanation of breaking 6 into halves (Goos et al., 2020). Specifically, the use of a table could be advised to provide the necessary visuals (see Figure 3 below).
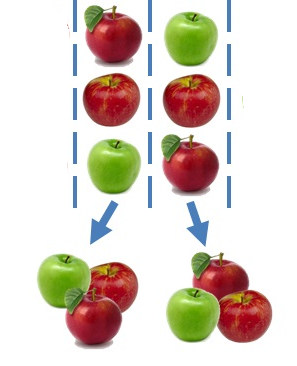
Another approach to assisting a student in managing the problem in question, particularly, the concept of splitting an integer into several parts, may require the use of a prop that is both visual and tactile. Specifically, a teacher may consider using an item that is easily split into several equal parts (Goos et al., 2020). Offering learners to take it apart and the input it together, a teacher will demonstrate the basics of division, which will be extrapolated onto the problem above.
1 /3 + 2 /5 = ?
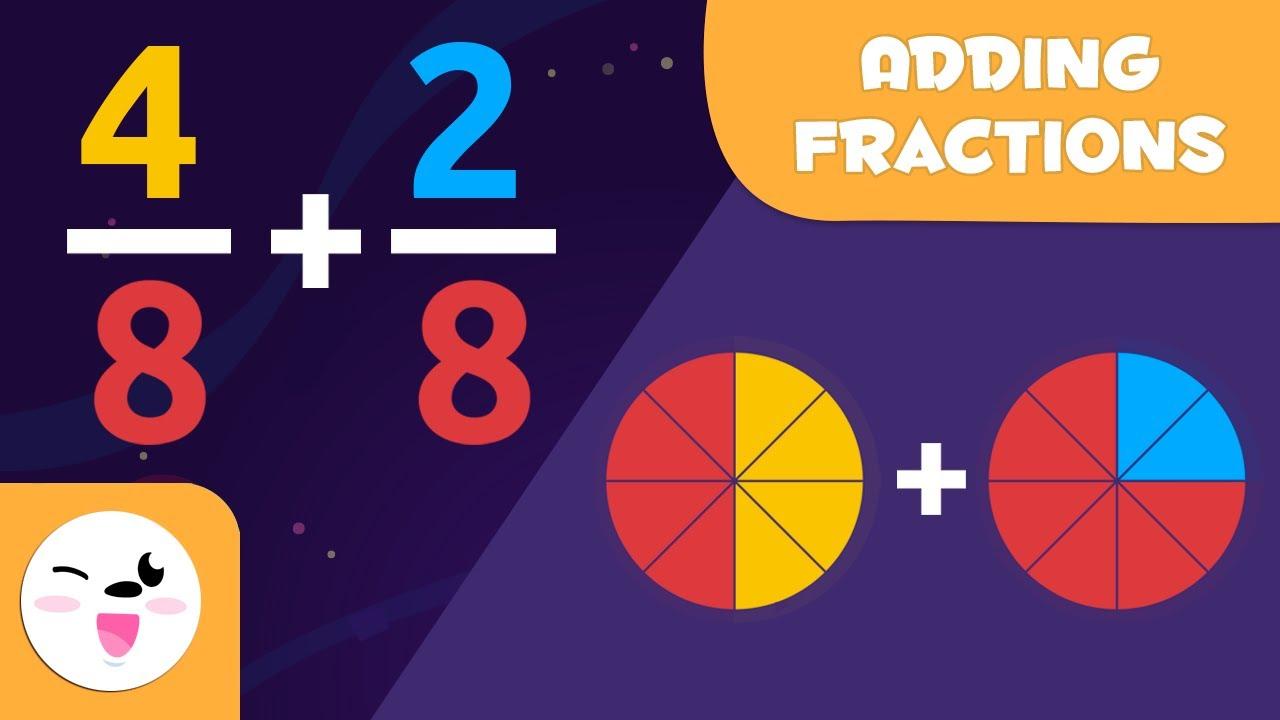
To teach learners to add fractions, several approaches can be utilized. First, the basic instructionalist approach may be adopted. Specifically, a teacher will explain that, for the addition process to happen, the denominator must be common. In turn, for the denominator to be the same in both fractions, the numerators must increase accordingly (Goos et al., 2020). Finally, the numerators should be added, with the common denominator remaining below.
Another approach that could be described as more illustrative may incorporate the use of several props. Specifically, a diagram depicting each fraction as a circle with the numerator being represented by a respective number of circle segments, and the denominator as the entirety of the segments, should be incorporated into the visual (see Fig. 3) (Goos et al., 2020). The specified visuals will guide the learners to the idea that, for the specified segments to be added, they need to match in their size, which, in turn, will lead them to the discovery of the concept of the common denominator.
¼ × 2 /5 = ?
In turn, introducing learners to the notion of multiplying fractions will suggest using two basic approaches. The first one suggests using the Area Model as the means of explaining the logic behind the increase in the integer (Goos et al., 2020). The latter phenomenon might seem counterintuitive to some students, which is why the specified framework is helpful (see Fig. 4). The use of color coding is particularly important to indicate the overlapping parts.

Another approach that will encourage an intuitive understanding of the subject matter would be to introduce students to the idea that the numerators and the denominators should be multiplied accordingly (see Fig.5) (Goos et al., 2020). The specified framework will represent an intuitively understandable approach that learners will be able to use.
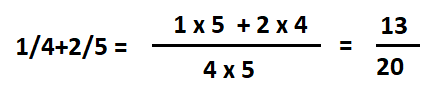
9 /10 ÷ 1 /5 = ?
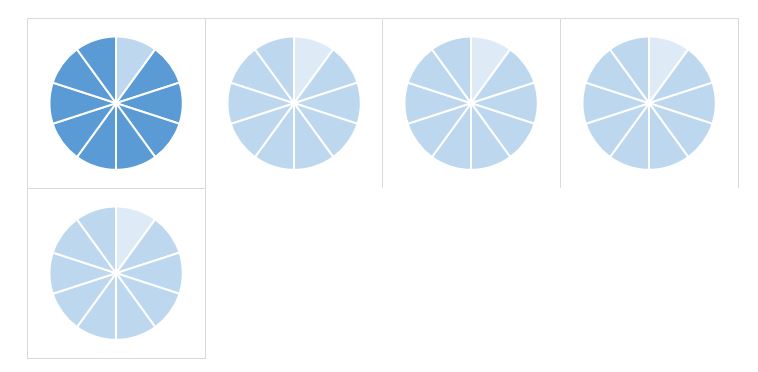
In turn, in order to teach students the essentials of dividing fractions, a teacher may adopt two key strategies. First, the teacher may explain that dividing the fractions requires flipping one of them “upside down” (see Fig. 6) (Goos et al., 2020). Specifically, the “Keep – Change – Flip” algorithm must be introduced.
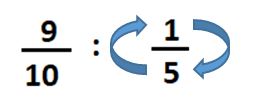
Another approach to explaining the concept of fractions’ division involves a though explanation of the mechanics of the flip. Specifically, the fact that the denominator of the divisor becomes the numerator of the dividend will have to be established (Goos et al., 2020). For this purpose, the Ghost Copy approach will be utilized.
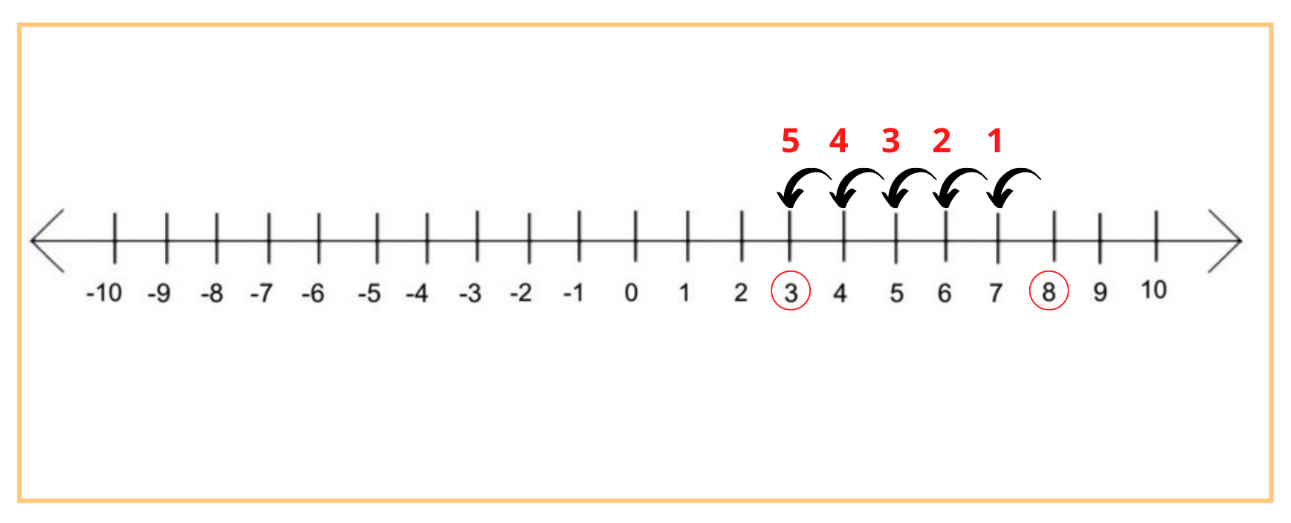
−0.3 − 0.03 = ?
Similarly to the second problem, the specified one can be approached from the perspective that building a numerical scale provides. Namely, by introducing a scale with positive and negative numbers, the teacher will be able to demonstrate that the specified equation requires shifting along the negative side of the scale, thus, decreasing the number to -3.3.
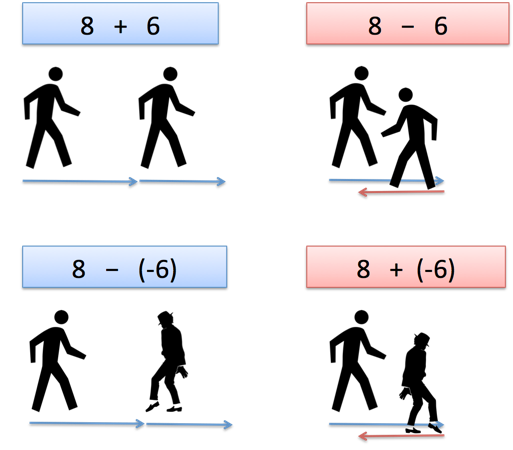
Alternatively, a teacher can utilize an approach that will allow viewing negative numbers as the opposite of positive ones, therefore, implying that the mechanisms of subtracting them involves reversing the approach used traditionally for positive numbers (see Fig. 9).
0.04 × (−2.5) = ?
The simplest approach to explaining the mechanisms of multiplying positive and negative numbers in the problem above represents teaching the student that negative numbers, when multiplied, produce a positive one, whereas a product of a positive and a negative number multiplication results in a negative one (see Fig. 10).
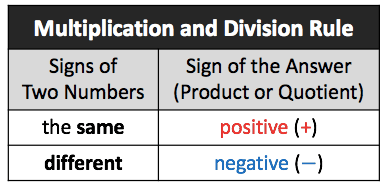
Alternatively, a teacher can use a simpler framework representing the same rule. In Figure 11, a student will have to multiply numbers right to left and bottom to top to obtain the required result.

−0.8 ÷ 0.04 = ?
Finally, the problem of dividing negative fractions will have to be introduced to students after addressing the concepts of negative numbers and fractions individually. To help a learner approach the problem above, a teacher will have to use a combination of approaches (Goos et al., 2020). These include the Keep – Change – Flip model and the positive and negative integers’ multiplication and division rule.
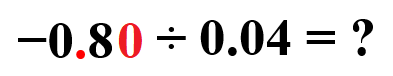
Alternatively, a teacher may represent the issue as a combined problem and, instead, produce a rule that incorporates the one for fractions division and negative numbers division. Specifically, a teacher may introduce the learner to the concept of moving the decimal point to the right or to the left depending on the divisor (see Fig. 12) (Goos et al., 2020). Afterward, the type of the integer (negative or positive) is identified by the learner.
By considering the combination of visual representations of the notion of positive and negative numbers, as well as the incorporation of metaphors as the tool for the described purpose, a teacher will be able to assist learner sin developing an intuitive understanding of the subject matter. Thus, not only can the problems provided above be solved effectively with the help of the specified approaches, but students will also be able to internalize the obtained information so that they could extrapolate it onto the further problem-solving process with a similar objective. The integration of metaphors and visual cues is essential in building an abstract interpretation and understanding of the studied phenomena in children, thus, allowing them to build a logical pattern of solving the specified equations. Thus, successful development of the necessary skills will be possible.
Reference
Goos, M., Vale, C., Stillman, G., Makar, K., Herbert, S., & Geiger, V. (2020). Teaching secondary school mathematics: Research and practice for the 21st century. Routledge.