At the beginning of the school year, I had fourteen students in my kindergarten class. Majority of the students were enrolled in a Montessori preschool program. Out of fourteen students, only three had joined from another school. The three students were given an early assessment test at the beginning of the school year to evaluate their mathematics skills. The results of the test indicated that one of the students had excellent basic math skills. Nonetheless, the other two found it difficult to recognize and to write basic numbers from 1 to 10. As a private school, the upcoming kindergarten students are expected to have at least the basic math skills such as counting and writing numbers from 0 to 9, as well as, to be able to add a few basic math facts.
The first lesson was based on the California State Standards 1.1 to 1.3, which focuses on learning with the aid of pictures. In this lesson, students were taught to sort and to compare numbers. In addition, they were taught to write numbers from 1 to 10. After the presentation of the lesson, the students completed exercises, which tested their ability to sort, compare, and to write numbers. The results of the exercises are presented in table 1 below. The average score in the sorting exercise was 88%. The students did not have any trouble in writing numbers from 1 to 5. This was demonstrated by the fact that all of them scored 100% in the writing exercise. The median score in most of the exercises was 99%. This implies that the students had some idea of applying basic number concepts. The main challenge that I noticed in the first lesson is that some students had trouble in holding their pencils. In addition, some of them were not able to concentrate in their work. Regarding the concepts that were taught during the lesson, some students could not easily compare numbers from 1 to 10. Concisely, understanding the concept of less than and more than was difficult to some students. Overall, the students’ performance was satisfactory as indicated by their scores in table 1 (an average score of 90% in all exercises). Consequently, I proceeded to the next exercise, which involved using Montessori sensorial materials to teach math.
Table 1. Initial Math Assessment Scores Based on California Mathematics Standard.
Following the completion of the first lesson, I was able to integrate the Montessori math equipment in the second lesson. Montessori sensorial items such as flowers were used to assess students’ sensorial skills. This involved evaluating the students’ ability to sort and to categorize the flowers into groups with similar features such as color. Most of the students were able to classify the flowers into different categories. Based on this hands-on-exercise, each student was assessed independently using questionnaires that were administered verbally. The questionnaires had ten questions. The maximum score per question was 10 marks. Table 2 presents the results of this assessment. According to the table, the average score in the sorting and categorization exercise was 95.29%. This implies that most of the students had mastered the skills that were taught in the sorting and classification lesson. Thus, we proceeded to the third lesson.
Table 2. Math Assessment Scores Based Upon Montessori Math Curriculum.
The third lesson involved using red and blue rods to teach math concepts. The students got hands-one-experience by touching and feeling the number values of fewer than or more than concepts. The teacher used the questions in appendix D to assess the students individually. The students were expected to demonstrate their knowledge of math concepts by answering the questions. The students were expected to know that each number represented a quantity. Additionally, they were expected to compare numbers between 1 and 10. The concept of odd and even numbers was taught with the aid of numeral counters. The lesson was repeated a few times in order to enhance students’ understanding. After explaining the concept of odd and even numbers, 10 questions were used to evaluate each student. The emphasis in this assessment was to determine if each child could place the counters under each number in order to illustrate the odd and even arrangement, as well as, to demonstrate the concept of less than or more than. Appendix D was used as the final evaluation for the students in the third lesson. All the students had a score of at least 3 out of the possible 4 points. Based on this result, I believed that the students were able to compare numbers and to differentiate odd from even numbers. Additionally, the results gave me the confidence to introduce the next lesson, which focused on simple additions and subtractions.
The lesson on addition and subtraction was taught using Montessori materials such as strip boards, as well as, the state recommended textbook. I used these materials to enable me to compare the students’ performance in addition and subtraction exercises in both the California State curriculum and the Montessori curriculum. In the California State curriculum, the students were taught using the recommended textbook without any hands-on materials. In this case, the students’ had a mean score of 81.50% in addition tests. After this evaluation, Montessori hands-on materials such as strip boards were used to teach the students about addition and subtraction. The same test that had been administered prior to the introduction of the Montessori materials was used to evaluate the students. In this case, the mean score was 94.50%. This means that the students’ performance improved by 13% after the introduction of the Montessori learning materials. Similar improvements in performance were noticed in the subtraction exercises. The limitation of these findings is that the students’ performance was also likely to improve if the Montessori materials were introduced first, followed by the California State curriculum. This is because spending more time on learning activities leads to improved performance. Nonetheless, the results suggest that the students’ competence in completing addition and subtraction exercises improved.
Having completed the lesson on addition and subtraction, I introduced the next one, which focused on the relationship between quantities and numbers. The materials used in this lesson included the hundred-board, the hundred-chain, and the ten-board. The lesson was also presented using learning activities such as the positive and negative snake game; counting teen numbers; and using the teen board to illustrate the relationship between quantities and number symbols. The assessments in this lesson were based on teacher-created rubrics, which are presented in appendix E. The results of the assessments are presented in table 3. Teen board assessment results indicated that out of 14 students, 13 scored above 85%. One student had a score of 56%. Thus, only one student required repetition and help with his class work in order to perform better. In the hundred-chain assessment, only two students scored below 50%. I reviewed the lesson a few times with the two students and assessed them again. In the second assessment, the students’ score increased from 45% to 75%. Only one student scored below 50% in the exercise that involved using the hundred-chain to count from 10 to 100. After reviewing the lesson, the student’s score increased from 45% to 75%. Almost all students excelled in the hundred-board counting exercise. They were counting with confidence and moved the number tiles very comfortably. The student who scored less than 50% was given more time to practice.
Table 3. Students’ Performance Based on Individual Assessments.
Before introducing the next lesson, I revised the previous ones and evaluated the students’ ability to apply the concepts that they learnt. The results of the evaluation are presented in table 4.
Table 4. Analysis of California Mathematics Standards – Formal Observation Based. On Individual Student Test Assessments.
We managed to complete all the benchmarks for the second quarter of the year. The assessments were done based on students’ performance in each lesson. Standard 1.0 through 3.0 lessons were conducted in quarter 1 and 2. During the lesson discussions, students showed interest in various textbook versions. The students learned through visual learning concepts and additional materials, which were provided by the publisher. The visual concept development in all the textbook lessons helped the students to acquire math skills and concepts by seeing ideas developed in visual displays.
Prior to the introduction of the next lesson, I administered a pre-test and a post-test to evaluate the students’ ability to define and to categorize objects. The pre-test was conducted before the introduction of Montessori sensorial materials, while the post-test was done after their introduction. The results are presented in table 5. According to the table, the students’ mean score increased from 75.57% to 91.79%.
Table 5. Pre-test and Post-test Assessment on California Math Standard on Algebra Functions 1.0-1.1.
In the second phase of classifying objects, the students had a firsthand experience in using colorful illustrations. The materials that were used included drawings, photographs, common objects, graphic organizers, number webs, and reference charts. The lessons involved a problem solving process in which the students asked themselves questions regarding the things they did and how they did them. After every week, the children were asked to check their work and analyze if the answers were reasonable. After, a critical review of the lesson I realized that the students’ performance was not very impressive. Consequently, I revisited the lesson plan and integrated Montessori sensorial lessons with classification activities that are correlated with the California State Standards. The students were allowed to practice on the same textbook concepts in a hands-on environment in order to improve their understanding.
Having completed the lesson on sorting and classifying objects, we proceeded to the next level of learning, which involved teaching students about time (clock), money, and factions. The lesson on fractions began with an explanation of why we study fractions and parts of objects. The children were given pieces of paper, which they were expected to fold into half in order to understand the concept of dividing things equally. The students were asked to recognize the shapes that they created by dividing the papers equally. They also had to complete the dotted paper and shape-drawing exercises, as well as, to divide shapes into equal parts. I applied the publisher-recommended test after completing the lesson. The test had 10 questions with each having ten points. The Montessori materials were introduced after the test. The first lesson was presented with the aid of apples, which were distributed to all children. The concept of a ‘whole’ was introduced first. This was followed by cutting the apple into half and telling the students a story about sharing things equally. In this lesson, the children learnt about the concepts of a half and a quarter as represented by ½ and ¼ respectively. Children were also introduced to tracing each inset on red construction paper and were asked to write the numerical concept beneath it. The assessment for this lesson involved giving each child questions with mathematical representations of 1, ½ and ¼ and asking them to cut a circle according to these fractions.
I also used rubrics in appendix D to evaluate the students. The rubrics consisted of evaluations that were based on Bloom’s Taxonomy, which focuses on knowledge, comprehension, and application. Each child’s competence in analysis, evaluation, and synthesis was assessed using a scale of 1 to 4. Only three students scored less than 60% in the California State assessment. Four students scored 100%, while another 5 scored above 80% in the Montessori assessment.
In the lesson on money, students were asked to use their counting skills to count coins. The state recommended textbook was used to supplement the student’s homework. The lesson was presented in a systematic manner. First, the students were introduced to the concept of one cent using red and blue number rods. Gradually, the cent numeral and its symbol were presented with the aid of number cards. The classroom was setup as a shop so that each child could practice the concept of buying things using a one-cent coin. This concept was used systematically until we reached 10 cents. We revised the lesson about fractions before introducing the concept of 25 cents. Using the fraction materials, as well as, the 25-cent and half a dollar coins, children were allowed to relate the idea of one whole to a dollar, ½
to half a dollar and ¼ to a quarter dollar. The learning outcomes were measured using a formative assessment rubric. Anecdotal evidence was measured using a scale of 1 to 4. Four students had a score of 4 in content analysis, which focuses on students’ ability to demonstrate, construct, order, and display. Two students had a sore of 4 in the content area of evaluation, which focuses on judgment, assessment, choice and forecast capabilities. Finally, four students had a score of 4 in the assessment of comprehension skills, which encompasses the ability to explain, retell, and show. Having completed this lesson, we proceeded to the next level, which involved learning about time.
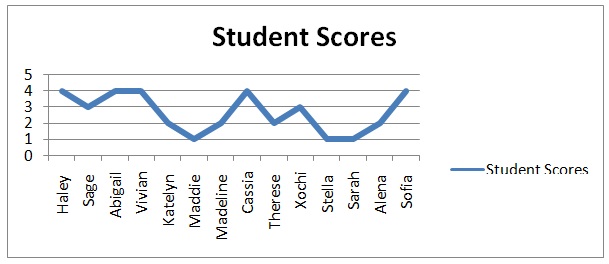
Fractions and time lessons consist of the conventional content that enables children to memorize time and counting. Children in kindergarten learn about regular and analogue clocks in order to read and understand time. I began the lesson on time by allowing students to discuss what they saw on the clock. I also had a discussion with the students concerning day and night, and the importance of using the clock to keep time. The rotation of the minute hand from 12 to 12 was explained using the concept of one whole. Students’ understanding was measured using scoring rubrics, whereas anecdotal evidence was measured using a scale of 1 to 4. The students’ performance in this assessment is presented in figure 1.
The last lesson focused on the use of concrete objects to determine the answers to addition and subtraction problems. The goal of this lesson was to enable the students to join and to separate small groups of numbers and to record the results symbolically. A pre-test indicated that only 10 students were eligible for this lesson, while the other four needed more time to improve their counting skills. The 10 students were divided into two groups and allowed to work with addition and subtraction boards. They were asked informal and random questions about the order of numbers. The learning outcomes were measured using anecdotal evidence rubrics. Since the results were not impressive, the lesson should be taught using a different method in order to enhance the students’ understanding.
The next level of learning focused on the use of Montessori hands-on materials to teach abstract and complex mathematics concepts. Some of the concepts that were taught at this level include division, multiplication, and identification of various geometric shapes. The materials used to teach the students included toys, golden beads, and the Montessori basic geometry cabinet among others.
The first lesson focused on matching and sorting circles, squares, and triangles given in concrete and pictorial forms. The objective of this lesson was to enable the students to identify and to match the pictorial forms of different shapes with the relevant vocabulary. The state standard that I used in this lesson was MG 2.1, which focuses on identifying and describing common geometric objects, and MG 2.2, which focuses on comparing familiar plane solid objects with common attributes. Regarding the recommended textbook lesson, I sorted the pictorial forms of different shapes using cutouts of the corresponding shapes. Furthermore, I used toys that had wheels; a few cylindrical objects, rectangular blocks and buttons; and counters and container lids to match the similarities in shapes. The lesson was introduced with the aid of a song titled ‘the wheels on the bus go round and round’. Each shape was presented with the help of the matching hands-on material. At the end of the lessons, the students were evaluated using the publisher recommended assessment. In this assessment, 4 students scored 100%, while 6 of them scored between 90% and 98%. The remaining 4 students scored between 85% and 90%.
Having completed the textbook lesson, I introduced the Montessori basic geometry cabinet. This cabinet is part of the Montessori sensorial curriculum that is used to teach children about the two dimensional or plane shapes. Prior to the presentation of the cabinet, the children were introduced to a tray, which had a circle, a square, and a rectangle. The presentation of the Montessori geometric cabinet began with the circle tray. Children were expected to trace the contours on the circles in order to feel the round shape. The tray consisted of six circles, which were arranged in order from the largest to the smallest in diameter. The second tray in the cabinet consisted of six rectangles. The largest shape in the tray was a square, which is a special rectangle. The remaining rectangles differed in terms of the sizes of their width. The third tray in the cabinet had six triangles. These included equilateral triangle, acute isosceles triangle, right isosceles triangle, obtuse isosceles triangle, right scalene triangle, and obtuse scalene triangle. The last two trays had irregular straight shapes and irregular curved shapes. The irregular straight shapes included rhombus, parallelogram, acute scalene triangle, trapezoid, and right trapezoid. The irregular curved shapes included oval, ellipse, curvilinear triangle, and quatrefoil. Children had the opportunity to trace, visualize, and to categorize the shapes in the trays, as well as, to relate them to real life objects. They also made small booklets for each tray, which they used to label each shape.
Prior to the introduction of the next lesson, I invited my co-teacher to observe my teaching. Her feedback was that I had clarity and knowledge in what I teach. Additionally, she evaluated each child’s learning using the items in appendix F. The evaluation revealed that six students were able to work independently, while another six were able to recognize shapes in complex formats. Moreover, two students had some understanding of special relationships between shapes. However, one student had trouble in identifying shapes. Consequently, the co-teacher recommended that I should redirect the attention of the student by allowing her to work with each tray for a few more weeks.
Having taken the recommendations of the co-teacher, I introduced the next lesson in geometry, which was about constructive triangles. As lower schoolteachers, we agreed to introduce lessons on triangles due to the inadequacy of the content provided by the textbook publishers. In this regard, I introduced the Montessori constructive triangle box, which has several triangles with different colors, sides, and angles. I also introduced two equilaterals that were separated with two black lines that faced each other. I identified three other figures as common parallelograms. A parallelogram refers to a plane figure whose sides are parallel. The students worked as a team to find the differences between parallelograms and other shapes such as squares and rectangles.
The second lesson was about parallelograms. In this lesson, I showed students that triangles with two sides of varying length could be used to form a square and a common rhombus. Moreover, I explained to the students that a rectangle and two parallelograms could be created using a triangle whose sides are not equal in length. The lesson was extended to the students’ homework packets. I assessed the students by reviewing their homework and making corrections to them. In addition, I had a special cover sheet, which had a survey section about the assignments. The purpose of the survey part was to obtain feedback from parents concerning the assignments. The survey results indicated that seven students were able to complete their homework without parental support, whereas five of them sought assistance from their parents. However, two students did not attempt to complete the assignments or seek help from their parents.
The completion of the lesson on geometry led to the introduction of the concept of length and size. This lesson was based on the California MG 1.1, which focuses on comparing the length, weight, and capacity of objects by making direct comparisons with reference objects. The main objective of this lesson was to teach students about measurement using the concept of length, height, and weight. By comparing the length of three objects, students learnt the concept of long, longer, and longest. Similarly, comparing the heights of three objects enabled them to learn the concept of tall, taller, and tallest. In this lesson, students were allowed to work in groups in order to share knowledge by interacting with each other.
The students’ performance in these activities was assessed with the aid of the self-evaluation rubrics in appendix G. The self-evaluations indicate that nine students worked well in their groups by assisting their colleagues to complete the activities. Three students indicated that they let their team members complete the activities and only helped when asked to do so. The remaining two students stated that they did not participate in the group activities since their colleagues did the work. I filmed the lesson during my presentations. A review of the film revealed that the two students who did not participate in the group activities were fighting around and had no interest in learning. Consequently, I revisited the lesson by presenting it to the two students and assessed their understanding using the items in appendix F. Generally, the students showed interest in learning. One of them had the highest score of 4, while the other had an average score of 3.
Having mastered the concept of measurement and related concepts such as height, length, and weight, the next logical step was to introduce a lesson that could enable the students to relate these concepts to numbers. Consequently, the next lesson was about numbers ranging from 0 to 30. This lesson was based on the California standard NS1.2, which focuses on counting, recognizing, naming, and ordering a number of objects up to 30. The main objective of this lesson was to enable students to count up to 20 by recognizing categories of tens, and to write figures from eleven to thirty. In this lesson, I integrated the Montessori golden bead tray with the hundred chains. Following the introduction of the Montessori hundred chains, the students found it easy to count up to 100.
Additionally, they got interested in using the hands-on materials on their own. The text material on grouping in 10s was incorporated in the students’ homework packets. The students also had the opportunity to explore the Montessori 100 chains on their own. During this exercise, I observed the students practice to count by grouping the beads in tens. I questioned the students randomly by asking questions such as show me, and what is this? The analysis of the data that I collected revealed that the students enjoyed the lessons and the accuracy of their learning was in the 95th percentile. I also used the students’ homework to assess their ability to work independently. According to the weekly parent information sheets, 12 students were able to work independently at home and only two students needed help.
Since majority of the students had mastered the concept of counting, it was logical to introduce a lesson on number bonds. This lesson was based on California state standard AF1.1. This standard focuses on identifying, sorting, and classifying objects by attributes, as well as, identifying objects that do not belong to a particular group. The objective of the lesson was to teach the students to find a total in a set that consist of several subsets. Additionally, the students were expected to know that stating the size of a subset could lead to finding the total of each set. The textbook activity involved using pictures to write two digits that make a given number. Thus, it was a perfect opportunity to introduce the children to the Montessori color bead box.
This box contained beads with different colors and were categorized in groups of 10. The students who had prior knowledge on Montessori math were able to recognize the box easily. Nonetheless, I had to revisit the Montessori basic color bead stair in order to enhance the understanding of the students who had no prior knowledge of Montessori math. Integrating the textbook lesson with the Montessori color bead box improved the students’ ability to understand the lesson. Since this was a new strategy, I invited the 1st and 2nd grade teachers to observe my presentation. According to our observations, the students were able to interact and to relate the number bonds to each bead category. For instance, if the bond was 15, the students showed 1 golden ten bar and blue bead bar from the box. The 1st and 2nd grade teachers also incorporated the color bead box in their lessons in order to make them more practical. Students’ learning outcomes were measured using appendix A. 9 students scored 4, whereas the remaining 5 had a score of 3. Based on the positive outcomes of this lesson, we held a discussion and agreed to incorporate the use of color bead box in our next year’s lesson plans.
The success of the lessons described in the foregoing paragraphs prompted me to introduce a lesson on simple math operations such as addition and subtraction. The standard used in this lesson was California NS 2.1, which focuses on the use of concrete objects to determine the answers to addition and subtraction problems that involve two numbers that are each less than 10. The lessons’ objective was to enable the students to use their math skills to perform addition and subtraction based on the same situation, as well as, to learn how to solve story problems that involve addition or subtraction. At the end of the lesson, I did a review and assessments using diagrams and story problems. Since this is the base lesson for additions that involve multiple digits, I focused only on the textbook content. The students worked as a class and I used the publisher recommended materials to solve story problems. The students were assessed based on their feedback in each lesson. Appendix D was used as the rubric for this assessment. 10 students preferred the pictorial lessons to doing rigid math from the board. The remaining 4 students preferred to act out every math problem because it helped them to solve the problems in a better way.
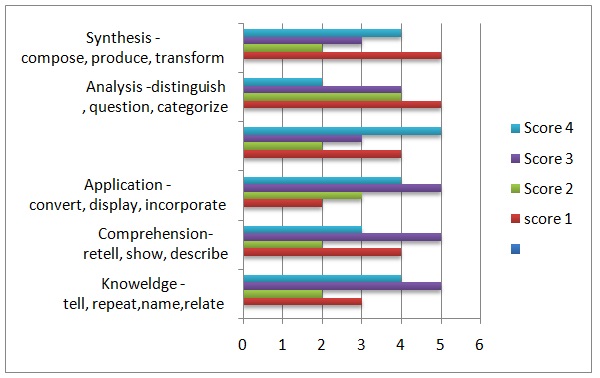
The lesson on simple addition and subtraction was the last one from the textbook. Thus, I had to introduce complex concepts using advanced Montessori materials. The first lesson focused on assessing students’ ability to learn in terms of five competencies namely, knowledge, comprehension, analysis, evaluation, and synthesis. In this lesson, the children were presented with the golden bead tray. The beads were arranged systematically from left to right in order to help the students to understand the concept of thousand, hundred, and ten. The students were assessed on individual basis. In addition, I performed a group evaluation by pointing at each category of the beads and asking the students to name them. The evaluation for this exercise was based on Montessori assessment rubrics. Figure 2 summarizes the performance of the students in this assessment.
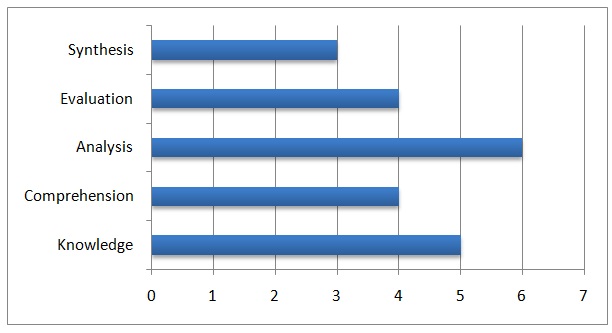
Regarding acquisition of knowledge, five students attained the highest score of 4 by providing correct answers to each aspect of knowledge, which include ability to tell, show, and to describe categories. In comprehension, four students had a perfect score of 4 by demonstrating a high ability to retell, show, and to describe. In the area of analysis, six students attained a score of 4 by providing the right answers in the assessment of ability to distinguish, question, and to categorize. In the area of evaluation, four students attained a perfect score of 4 by demonstrating a high ability to judge, verify, choose, forecast, and to estimate. Finally, the assessment of students’ competence in synthesis, three of them scored 3 by correctly answering questions that relate to ability to compose, create, produce, and transform. Overall, ten out of fourteen students scored 3 or more in at least three areas that were covered by the assessment. This means that 90% of the students excelled in the assessment. Following this success, I proceeded to the next lesson that involved the formation of numbers.
Formation of Numbers
This lesson involved instructing students to arrange a set of cards and selecting one of them. The selected card was given to one student who kept it in her tray. In order to determine if the students understood the concept, I asked them to collect the quantity of beads that were corresponding to the figure written on the card. After a few repetitions, the activity was reversed. This involved giving students a specific quantity of beads and instructing them to select the card, which had a figure that corresponded to the quantity of the beads. I did the assessments continuously by having a discussion with each child concerning their work. This included the following activities. To begin with, students were requested to put back the items in their trays repeatedly. After understanding the concept, they were given two cards with numbers such as 20 and 3. The students were expected to name these numbers.
For instance, they were expected to state 2 tens and 3 units in reference to cards labeled 20 and 3. After naming the numbers, the students were asked to collect the amount of beads that corresponded to the numbers on the cards. This task was done again using the cards that represent the hundreds and the thousands. After several repetitions, the activity was reversed by giving the students some beads and requesting them to identify the card with the corresponding number written on it. The assessment was done at each step of the exercise. The direct aim of this lesson was to enable students to name large numbers. Its indirect aim was to illustrate the hierarchy of numbers. Even though the basic numbers range from 1 to 9, their importance in terms of units, tens, hundreds, and thousands stems from their positions within complex numbers.
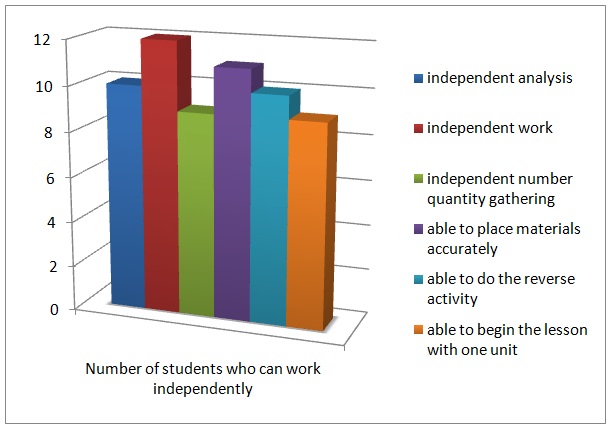
Since the students were evaluated on a continuous basis, I used a formative assessment rubric to measure their understanding of the concept of numbers and quantities. Figure 3 presents the results of this assessment. According to the chart (figure 3), most of the students were able to work independently. Nonetheless, some of the students were unable to relate quantities to various numbers. In particular, the ten and the hundred number cards confused some students. Even though the score on the assessment of independent work was above 95%, I will have to repeat the exercise until all students score 100%. Having completed the lesson on number formation, the next logical step was to introduce the concept of addition using golden beads.
Static Addition Using Golden Beads
The materials used in this lesson included 3 boxes with small cards, which included a set of 9 units, 9 tens, 9 hundreds, and 3 thousands. I also provided a box of cards with numbers from 1 to 9000; several loose unit beads, ten-bars, hundred squares, and thousand cubes; 3 trays and 3 little bowls for the loose beads; and a large tray with an extra bowl.
At the beginning of the lesson, I asked one child to arrange the large cards on a mat, and another child to lay the beads on a different mat. In addition, I asked the children to separate the two mats with three small mats. I also instructed the students to organize their set of small cards in a pattern similar to that of the large cards. However, they were to limit the range of their cards to 1000-3000. The students also placed three trays on the third large mat. After the completion of this exercise, I requested the students to place their trays on the mats. Additionally, I asked the students to select one of them to pick cards for 2 units, 3 tens, 2 hundreds, and 3 thousands. The students were expected to keep the cards in their trays. In order to ensure that the students understood the procedure, I helped them to verify the units, tens, hundreds, and thousands that were on their cards, before instructing them to collect the corresponding amount of beads.
After each child returned, I verified what they had by requesting them to count the beads that they brought. Once the verification was complete, I directed the students to superimpose their cards. Furthermore, I requested them to read the numbers with me in order to confirm that they had 2 units, 3 tens, 2 hundreds, and 3 thousands. This task ended with the students confirming that they had 3232 beads. A repeat of the lesson was conducted after the students completed the verification of their beads. The students worked on the lesson individually for a few weeks. Evaluations were conducted after the completion of the small group activities and the results are presented in table 6. According to the students’ evaluations of their learning, majority of them had gained knowledge by collaborating to solve math problems. Consequently, I introduced them to the concept of dynamic additions.
Table 6.
Dynamic Addition
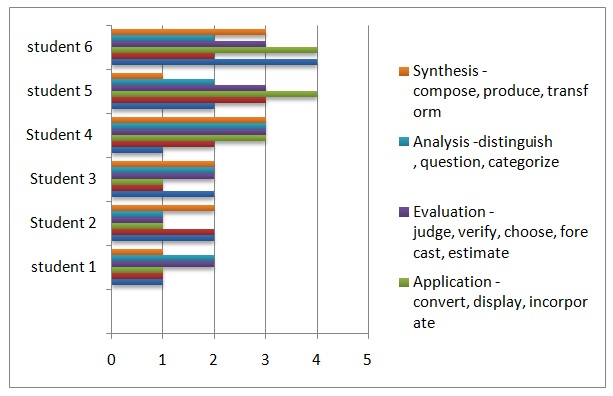
The introduction of this lesson was similar to that of the static addition. However, the children were required to take cards in problems that required carrying over. These problems could include numbers such as 3323, 2456, and 1345. The students repeated all the steps involved in static addition. This involved counting from 1to 10 and replacing ten units with a ten-bar. Moreover, I asked the student to count the remaining units and to collect the card that had the corresponding number. I repeated the lesson using cards for tens, hundreds, and thousands. The aim of this lesson was to teach students about addition that involves small numbers that can be combined to create a larger one. I administered a continuous evaluation after completing the lesson in order to determine the number of students who had mastered both static and dynamic addition, and were able to work independently. The results of this evaluation are presented in table 7. The assessment was based on appendix D and focused on five capabilities namely, comprehension, application, analysis, evaluation, and synthesis. The results reveal that the lesson should be reviewed so that all students can improve their knowledge. Having completed the lesson on dynamic addition, I proceeded to the next lesson, which focused on the use of golden beads to perform static multiplication.
Table 7.
Golden Beads and Static Multiplication
The set up of materials in this lesson was similar to that of addition. The presentation was also similar to that for addition. This involved determining the number of the available beads, collecting the students’ small cards and arranging them just as we did in addition lessons. During this exercise, the students realized that they had the same amount of beads. The next step involved taking 1223 three times and explaining to the students that the result was equal to 3669. I introduced the number concept with the word multiplication. The assessment for this exercise was done with the aid of appendix E. Individual assessments were done using five questions, with ten points each. Based on the outcome of the assessment and the students’ interactions during the lessons, I was confident to introduce the next lesson, which involved subtraction using golden bead materials.
Static Subtraction with Golden Beads
The procedure used in this exercise was similar to that used in addition. The only difference is that a fourth set of cards with numbers up to 9000 and a small mat to place them were included. In addition, I defined and explained three terms namely, minuend, subtrahend, and different. The students repeated the tasks used to complete the addition assignment by counting the units, tens, hundreds, and thousands. Following the completion of the counting exercise, I requested the learners to select the card with the corresponding figure. The students superimposed the cards in order to get the number 7879. I requested one learner to determine the number of beads that were on the mat and to pick the corresponding small cards to represent them.
After superimposing the cards, the learners obtained the figure 4456. In order to illustrate the subtraction operation, I reiterated that we had 7879 beads at the beginning of the process. However, some beads were given away during the process. The illustration involved placing the cards that represented the beads that were given away (3423) below 7879. The new total was placed below 3423. Thus, I explained to the students that we lost 3423 beads, thereby remaining with only 4456. Moreover, I explained to the students that this exercise is what subtraction entails. Having mastered the static subtraction, I introduced the concept of dynamic subtraction. I used continuous assessments to evaluate each student’s skills and understanding. The result indicated that nine out of the fourteen students were ready to proceed to next level of learning, which involved static division with golden beads.
Static Divisions with Golden Bead Materials
The materials used in this lesson were similar to those used in the addition exercise. However, the small cards had numbers of up to 9000. I asked one student to bring her tray to the supply mat and pick cards for 9 units, 3 tens, 9 hundreds, and 3 thousands. I used the idea of sharing things fairly to enable the students to understand the concept of division. The students advanced to the next level of division after the number concepts were superimposed. This involved explaining to the students that dividing the number 3393 must begin with the thousands. The lesson was presented in a group setting and the instructions were given as follows. To begin with, I gave each child the cards for 1 thousand. I instructed them to count the number of thousands they had in order to ensure that they had the same number. After completing this task, I instructed the students to pick the card that represented 1 thousand. The task was repeated to ensure that each child had 3 hundreds, 1 ten, and 3 units. Finally, I explained to them that they would get 1313 by dividing 3939 by 3. These procedures were used to explain the concept of dynamic and long divisions.
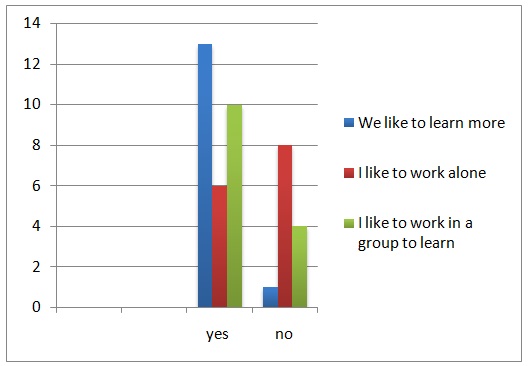
The main objective of teaching the concept of short division was to enable the students to understand the nature of division. The students were expected to understand that a large object could be split into smaller and identical parts. The other objective of the lesson was to illustrate the distribution of quantities in long divisions. The students were expected to understand the categorization of divisors and to realize that the solution to division problems is often the portion of an object that an individual receives when it is divided equally. Since understanding the concept of division is challenging at this stage, I decided to allow the students to progress with the learning at their own pace and capabilities. The assessment for these lessons involved completing a work reflection exercise by each child. The results of this assessment are presented in figure 4. The results reveal that most of the students enjoyed group work rather than working independently.
Having completed the lessons that focused on the use of golden beads, I shifted to the use of stamp game to teach various math concepts. The presentation began with an explanation of the color and quantity of the stamps. The strategy in this lesson was to move progressively from concrete to abstract concepts. I explained to the students how to write problems using symbols. The lessons were presented on a one-on-one basis. Moreover, they were based on the elementary math manual. The lessons involved teaching both static and dynamic additions. The students were evaluated using appendix D and the results are presented in figure 5. After analyzing the results of the assessment criteria, I realized that the lesson should continue up to the end of the year in order to improve learning outcomes.
Static and Dynamic Subtraction Using Stamp Game
The static and dynamic subtraction lessons were based on the 6-9 Montessori math manual. Based on students’ reactions during the presentations, I realized that the lesson was confusing to some children. Concisely, they had trouble in understanding facts that were presented in an abstract manner. Consequently, I had to revisit the lesson on subtraction using golden beads in order to remind the students about the basic facts of subtraction. The students were evaluated using the rubrics presented in appendix D. The results indicate that six students excelled and were able to move from static to dynamic subtraction.
The score for these students ranged from 3 to 4. Nonetheless, eight students were not able to proceed from the static to dynamic subtraction. The six high performing students were introduced to multiplication. In static multiplication, the students were divided into groups of two and were taught to use symbols to perform multiplication. This lesson was based on the Montessori 6-9 mathematics manual. The evaluation for this lesson was based on appendix D. Students who scored in the range of 3 to 4 were allowed to proceed to the dynamic level of multiplication. Figure 6 illustrates the performance of the students in both static and dynamic stamp game multiplication. The multiplication lessons were followed by lessons on divisions.
Dynamic Division: 3 Level Divisors
In this exercise, a green circle was used to represent the missing units. Thus, I explained to the students that the green circle was used because the position of the units had a zero. I repeatedly asked the students to state the figure that would occupy the unit’s spot if it were not a zero. Prior to the presentation of new tiles, I shifted the green circle towards the bottom. After completing the presentation, I reiterated that division is concerned with the determination of the portion that a person gets when something is divided equally. In order to illustrate this point, I divided the ten skittles into ten units. Generally, all the fourteen students enjoyed the lesson. The success of this lesson led to the introduction of dynamic division.
In this case, I reminded the students of some basic procedures and the instructions were given as follows. To begin with, I requested the learners to take the learning materials and to work with me. After formulating a question that involved dividing 6525 with 5, I instructed the students to form the numeral 6525 with the aid of the tiles. I also reminded the student that division begins with the thousand in order to get the right answer. I gave each skittle a thousand. Thus, I remained with one thousand, which I converted to ten hundred tiles. All the hundred tiles were distributed to the skittle. In this regard, no hundred tiles were left after each skittle received 3 of them. All the unit tiles were distributed to the skittles. Finally, we counted the tiles that were distributed to each skittle, and wrote down the answers. The students were required to master the steps used in this exercise in order to solve division problems on their own.
In the next exercise, the students were expected to perform the division without any reminder. I began by creating for the students a problem that involved dividing 6738 with 5. The students were expected to repeat all the steps in the exercise on dynamic division with reminder. After completing the task, we realized that not all tiles had been distributed. However, the remaining tiles were not enough for all the skittles. Consequently, I explained to the students that the remaining tiles are referred to as the remainder. Moreover, I demonstrated to them how to write the word ‘remainder’. The next lesson was about teaching students to solve division problems with two divisors. In this activity, the instructions were given as follows. I invited the students to present the learning materials on the table and to work with me. Furthermore, I created a problem for them to solve. In this regard, I instructed the students to form the number 4583 using tiles and discussed with them the number of units in 12.
After this task, I presented two green skittles and explained to the students the number of tens in 12. In order to illustrate the concept of division, I put a blue skittle next to the green one and assigned to it a thousand tiles. The next step involved explaining to the students that whenever one 1000’s tiles are issued to the blue skittle, every green tile must receive one 100’s tiles. For every hundred tiles that I gave to each green skittle, the blue one received a thousand. The distribution of the tiles continued until there were only two 1000’s tiles and one 100’s tiles left. At this stage, I converted one of the 1000’s tiles into ten 100’s. Consequently, I was able to complete the distribution by issuing an additional 1000’s to the blue skittle, while the green ones received two 100’s tiles. After completing the distribution, I reminded the students that division is concerned with what an individual gets. Finally, I instructed the student to count the tiles that each green skittle received, as well as, to write the amount in terms of tens, hundreds, and thousands. Additionally, I requested the student to record the reminder in order to understand its significance.
Having completed this lesson successfully, we proceeded to the next one, which involved dynamic division with 3 level divisors without the tens. The procedure that was used to teach this concept was similar to the one used in the previous lesson. A blue circle was placed in the position of the skittle because there were no tens. I occasionally asked the students the figure that would represent the tens if it were not a zero. The correct answer for this question was one hundred fold less than what the hundred skittles would receive. In this lesson, the students were allowed to work independently by creating appropriate division problems and solving them using the procedure that had been presented earlier. The main objective of this lesson was to enable the students to solve problems that involve divisions on their own. The procedures used in this lesson were used to teach the students the concept of long division. The importance of using symbolic materials to teach division is that it enables students to understand abstract concepts easily. Due to the complexity of this lesson, we discussed as a faculty its suitability to the students. We unanimously agreed to incorporate it in the year’s plan for the kindergarten and 1st grade lessons. This is because the students showed a great interest in learning with the aid of the hands-on materials that were used in the lessons. After completing this lesson, we proceeded to the multiplication bead.
Multiplication Bead
The first presentation focused on the students’ ability to recall the multiplication tables. This form of multiplication is important due to two reasons. First, it explains the fact that the multiplier is not a solid body as used in the multiplicand. This enables students to understand that solving multiplication problems involves taking a given number several times in order to find the right answer. Second, it illustrates the fact that a sequence of lines forms a surface. The main objective of the lesson was to train the students to solve division problems. Additionally, the flexibility associated with the exercises in this lesson was expected to enhance the students’ ability to discover new facts. The indirect objective of this lesson was to prepare students for the future lessons that are related to geometry and algebra.
There was no recommended textbook material for this lesson because its content is beyond the grade level. Nonetheless, the multiplication bead board was a wonderful learning tool for the children. Using these materials can help us to understand why symbols only make sense to students who have had sensorial experience. The study of math often becomes dry and meaningless when educators eliminate the use of real objects in teaching math concepts. According to Montessori’s philosophy, enhancing a child’s sensorial experience involves improving their natural interest in mathematics. I presented this lesson in a group setting on a weekly basis. Since most 1st and 2nd grade teachers can present this lesson, I invited two teachers to observe my presentation. After the presentation, we held a meeting and discussed how we could incorporate the lesson in our curriculum. According to our agreement, I was expected to introduce the lesson’s materials in kindergarten by the third quarter of the year. The other teachers were to integrate the materials with the recommended text in the 1st and 2nd grade.
The multiplication bead board is an important asset to students who are interested in practicing to solve various math problems. I provided enough boards in order to enable all children to explore and to memorize the multiplication concepts. Based on the students’ learning abilities, I introduced board 3, 4 and 5 on an individual basis. Regarding the memorization of multiplication tables, the charts facilitated repetition, which enabled the students to master the multiplication facts. I conducted random evaluations of every child’s progress with the learning during the lessons. My observations revealed that the students enjoyed learning the concept of multiplication. I did not conduct a formal evaluation for this exercise because I believed the students were not ready for it. Generally, the multiplication bead board is a great learning tool. This is because it gives students in kindergarten an opportunity to explore various concepts in mathematics.
Following the completion of the textbook lessons and the presentation of the use of the materials described in the foregoing paragraphs, I focused on introducing a set of new materials in order to enhance the students’ knowledge in math. The materials were introduced on a continuous basis. Moreover, I filmed my presentation during the introduction of these materials. I invited my co-teachers to participate in the presentation of the new materials. The feedback of the co-teachers was that the materials should be included in the 1st and 2nd grade in order to improve learning outcomes. The first material was the unit division board, which was used as follows. I wrote several equations on the board, and explained to the students how they could be solved. The students were expected to follow the presentation in order to solve the equations on their own. After the students completed the assignment, I re-read the equations and underlined them in red without any reminder. The students were expected to record all the equations in a squared paper without any reminder. The direct objective of this lesson was to familiarize the students with the various methods of performing division operations.
The second lesson involved the use of division charts 1 and 2. The purpose of this lesson was to illustrate the concept of division combinations. Concisely, it involved determining the common factors and multiples in the division problems. The materials used in the lesson included division chart 1 and 2 and a basket for the charts. The division problems that the students were expected to solve were printed on blue tickets and placed in the baskets. The other materials were squared papers, pencils, and a blue box, which contained the answer tiles for chart 2.
The presentation for chart 1 was conducted as follows. I sat with each student at a desk and studied the board with them by helping them to find out the figures that were located in the top row. White color was used to distinguish prime numbers from the other digits on the board. The students were expected to examine the figures on the diagonal in order to identify the division sign. They were also expected to determine the correct answers to the questions by reading and writing them. The students were instructed to use their fingers to find the dividend, the devisor, and the division sign on the boards. I in order to find the correct answers to the questions, I instructed the students to move their fingers downwards until they reached the row in which the left finger was located. Finally, I asked the students to move their left fingers across the board. The answer was located at the point at which the left and the right fingers met. After a few repetitions, the students were expected to follow the same procedure to solve division problems on their own.
Chart 2 was used to teach the students about division with the aid of the following instructions. To begin with, the tiles were organized in an ascending order from one to nine. In addition, similar numerals were put in the same category in order to differentiate them from other numbers. The students were expected to identify a problem and use the tiles to find its solution. This process involved moving both the left and the right fingers on the boards in order to find the correct answers to the questions. The answers were found at the point at which the students’ fingers met. After a few repetitions, the students were expected to perform the exercise on their own. I extended the lesson by explaining to the students the meaning of prime numbers.
The third lesson focused on the transition from concrete to abstract concepts. This lesson was taught with the aid of the dot game. The purpose of the lesson was to explain to the students the concept of the decimal system. The materials included a squared paper with several columns, which were used to enter the values for the units, tens, hundreds, thousands, and thousands. The columns were split into smaller squares in order to create ten columns in every row. In addition, the columns had specific areas, which were set aside for recording the dots and the results of the counting process. Furthermore, an extra column was included and used to record all the questions. Apart from the squared paper, pencils and rulers were also used during the presentation. During the presentation, the students were expected to enter the addends and dots in the right rows and columns of the squared paper. After counting the dots, the answer was read and written below the addends. The students repeated the exercise by following these procedures.
The fourth lesson was meant for students who are between 5 to 5.5 years. It involved using small bead frames. The direct purpose of the lesson was to summarize the facts about the decimal system and to revise all the math concepts. The main material was a frame with four wires on which several beads were fixed. In the presentation, the students were introduced to the bead frame and the notation paper in which the number of beads were to be written. The beads were counted and recorded on the paper. The same procedure was used to illustrate the concept of dynamic addition, static subtraction, and dynamic subtraction in three different exercises.
The last lesson targeted students who were aged between five and six years. This lesson focused on multiplication and its direct purpose was to revisit the decimal concept. It also enabled the students to apply the concepts they had learnt earlier. The indirect purpose was to prepare the students to understand the distributive law of multiplication, which involves the analysis of numbers in terms of their hierarchical values. The materials included pencils, rulers, and a frame on which beads were fixed. I explained to the students the sections of the squared paper and the purpose of the bead frame. Additionally, I explained to them that we could record the number of beads directly in the right column of the notation paper. We continued to count the beads up to 1000 and recorded all the answers. These procedures were used to explain the concept of dynamic addition, static addition, and static subtraction. In conclusion, the students enjoyed learning using the new materials in all lessons. Since these materials led to improved learning outcomes, I recommend their use in teaching mathematics in order to enhance the performance of both straggling and advanced students. Concisely, they can lead to improved performance among students with different learning capabilities.