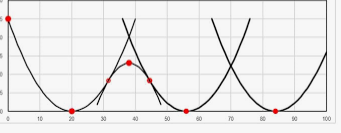
Parabolas are u-shaped curves that are mirror-like, or in other words, they are symmetrical. A continuous parabola lacks endpoints because it is infinite, facing upwards, downwards, left or right. Two aspects can describe a parabola: the focus and the line. The other name for focus is a “point,” and the other name for a line is the “directrix.” According to Saravia (2018), a parabola has a vertex, where it is a place where the axis of symmetry intercepts. Some of the characteristics of a parabola are that if made of shiny / reflecting materials, the light travels in a parallel direction with the axis of symmetry, and it is reflected in the parabola’s focus. Parabolas may face upwards or downwards and may also intercept at the x-axis, meaning that it has x-intercepts (Saravia, 2018). At times, parabolas may not have x-intercepts if it does not intercept the x-axis. Parabolas will always have y-intercept regardless of the direction they open or intercept.
Parabolas that open facing upwards always have positive coordinates, and they are said to form a smile. On the other hand, parabolas that open downwards always have a negative slope or coordinates, and they are said to form a frown. A quadratic equation must contain a squared variable to get an illustrative graph. For instance, y^2=20 or x^-8y=0 Parabolas are present in everyday life. For instance, a roller coaster is an example of a parabola in real life. Roll coasters are arcs that form facing up and down. When the roller coasters fall from the peak, they form a parabolic shape (Saravia, 2018). The importance of this parabolic shape is that it helps reduce air resistance which would resist the movement of the roller coaster. The other purpose of forming a parabolic shape in a roller coaster is that it attracts gravitational pull, which is essential in the movement of the roller coaster in a circular direction.
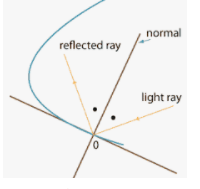
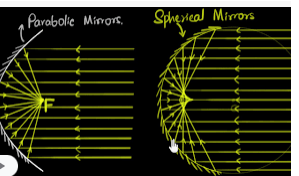
Another example of an actual life application of parabola is that they are used as reflectors to focus light. This is applicable primarily in a car, motorcycle headlights, and torches. Parabolas are an improvement of spherical reflectors that could increase the brightness but only give a beam of light over short distances, which cannot be used in driving vehicles at night. After advancement and the introduction of parabolas, the beam of light could be focused over long a distance, which was better off while driving vehicles at night. In the attempt to get the perfect parabola, several experiments were carried out. Saravia (2018) says that the first parabola to be created was a lighthouse reflector that formed the basis of the lighthouse in 1738 in Sweden.
The aim of creating a parabola was to reduce the wastage of light. In the modern world, parabolas have advanced from glass to electric parabolas. The electric ones were a combination of lighthouses and glass parabolas (Saravia, 2018). Parabolas can also be used in satellite dishes and flashlights, apart from cab headlight reflectors. For the case of satellites, parabolas help in the reflection of both television and radio signals and collect them as a beam, transferring them to the reception. The receiver then functions by intercepting the signals, which are then transmitted to televisions and radios as channels. The advancement in technology has helped a lot in communication since it is through the satellites that telephone communication has been made possible.
Reference
Saravia, J. (2018). what we’ve learned in our algebra 2 class about parabolas, using yewno definitions and concepts. Design Thinking Applied Mathematics, 1(3).