Letter of Summary
In this paper, we report on how to solve the famous Pizza Box Problem. The analysis starts with a brief description of the need to solve the Pizza Box problem and then proceeds to a discussion of the optimization concept. An analysis of the Pizza Box problem then follows using the required mathematical formulas and procedures. The results and discussion part follows the analysis section. In this section, we discuss the relevance of mathematics in solving real-life solutions and the pioneers of such mathematical techniques. In addition, we study the need for calculus and pre-calculus lessons for students. This is then followed by the conclusion section.
Body
Most companies and organizations have been faced with the problem of finding the maximum volume of a box that is constructed from rectangular pieces of cardboard. This problem involves sticking equal squares from each corner of the rectangle and then folding up the resulting sides as described by Dundas (1984). This kind of problem can be solved through an expert application of Calculus. Undeniably, calculus can be useful in devising efficient as well as practical construction approaches. In this report, we describe the application of Calculus in solving of the pizza box optimization problem.
One of the grand uses of calculus in the real-world setting is optimization. According to Daley, Gutierrez, and Wilkerson (2015), optimization is a concept that requires the use of minimal materials for maximum effect. In this case, the use of minimum cardboard material will be used to manufacture a pizza box having the largest volume. Calculus can be used as a tool to maximize, or in some cases minimize (technically referred to as optimize) a situation. According to Delfour and Zolésio (2001), getting a higher volume or occupancy rate of a given container is a vital goal for most businesses dealing in packaging and shipping of goods. Manufacturers and Pizza firms have to ensure the products fit in the 3D box vessels having optimal placement in order to ship or transport products at the lowest cost possible. The main problem of fitting the products is often referred to as a 3-dimensional packing problem (Eley, 2002; Pisinger, 2002). Notably, the overall effect is a reduction in the production cost of the container or pizza box, as well as a reduction in the cost of transportation or shipment.
Normally, optimization as well as heuristic approaches have been applied in solving Pizza Box optimization problems/issues. In 3D packaging problems, some studies assume the existence of an unlimited capacity (Electric Teaching, 2013). As noted by Dundas, most calculus students have been faced with the problem of finding the optimum volume of a box that is constructed from rectangular cardboard pieces by cutting equal squares from every corner, and then, folding up the cardboard’s sides (1984). The most suitable method of construction is shown in figure 1 on the next page.
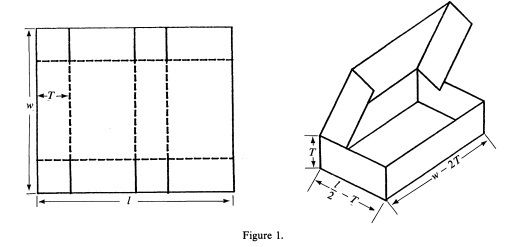
If we cut the cardboard along the solid lines and then appropriately fold it along the dotted lines then the use of appropriately-placed staples can secure the box to be fairly usable. In order to construct the pizza box, we adopted a no-top construction methodology by cutting out T by T-long squares from the cardboard’s rectangle having a length I as well as width w, where w < I. The ensuing volume is given by the following formula:
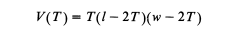
For a value of T < w/2, for the Pizza Box construction, its volume is computed as follows;
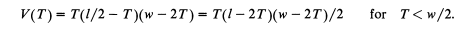
In this problem, we consider the value of T, which is the volume of the box, to be half as large by means of the Pizza Box technique, and the maximum is considered to occur at the same value of T in all of the cases. With a little iteration, researchers have found that restricting the rectangular piece of cardboard’s shape effectively limits the box’s maximum volume (Daley et al., 2015). However, this is not applicable in a real word situation. In order to allow for variable rectangular pieces’ dimensions as well as various sizes of the corner pieces, calculus must be used and it must involve various variables. The approach that was considered for this process was as elaborated in the next paragraph.
Suppose cardboard of A square inches is to be used for the construction of a Pizza Box by means of the Pizza Box methodology and fixing the height of the Pizza Box at T inches, we must find the dimensions of the rectangle that if used would optimize or maximize the volume of the Pizza Box (Optimization Problem, 2011).
From figure 1, we can take w to be equal to A/l. In other words w=A/l. Therefore, we shall have the following;
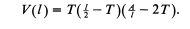
We then take the value of V'(1) = 0 whenever the value of I = m. Therefore, the required dimensions for the cardboard are
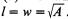
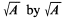
cardboard, we would like to find the required height, T, which would optimize this volume. Therefore we begin as follows;
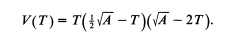
Therefore,
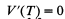
for
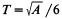
, and the optimum volume for the Pizza box is given by the expression
For this exercise, we use hypothetical dimensions for the Pizza Box problem. We use the area A of the box to be 144 square inches since this gives us a maximum volume of 64 cubic inches whenever I = w = 12 and the height, T = 2. The other method similar to the Pizza box problem method is the Popcorn Box method but that is beyond the scope of this report (Daley et al., 2015).
As noted in the analysis section, the Pizza Box optimization problem often obtains its solution from both the heuristic and optimization techniques. In 3D packaging problems, some studies assume the existence of an unlimited capacity (Electric Teaching, 2013). As noted by Dundas (1984), most calculus students have been faced with the problem of finding the optimum volume of a box that is constructed from rectangular cardboard pieces by cutting equal squares from every corner and then folding up the cardboard’s sides. In this section, we also discuss some of the discoveries and mathematical expressions that have allowed problems such as the Pizza Box problems to be solved. The pre-20th century saw great events that brought about various inventions and discoveries, especially in the mathematics field. There were various people who made great contributions to the mathematics field which are applicable and still in use to date.
Therefore, this paper will look at two great events and the contributors to the events in the mathematics field. About 250BC, there were various inventions and contributions by Archimedes who were considered as one of the great mathematicians in history. He is still honored for the various contributions he made in geometry, mechanics, physics, and technology. Another contribution was the discovery of how to find the volumes of spheres, and he went ahead to discover the exact pi value, which he calculated as well as devised the notion of mathematical exponents. A Greek letter, Pi, is used in describing ratios of diameter as well as the circumference of a circular object. He pinpointed pi value as being between 3-10/71 and 3-1/7. He arrived at this value by the inscription of a-96 sided polygon inside a circle. The discoveries were published in the measurement of the circle. He also discovered the principle of buoyancy. When he discovered it, he went out shouting Eureka in the streets. This was the principle of water displacement that he discovered when he was bathing (Ferris, 2010).
Moreover, he made it possible to find out the area bounded under a parabolic curve. He came up with the idea of using extraordinarily creative reasoning involving constructing an infinite number of triangles inscribed in a circle that takes up the area that was in the parabolic part. Markedly, this contribution was of great importance particularly to Isaac Newton who developed calculus (Films Media Group & KM Media, 2011). He also found out how calculations of areas of circles could be done as well as establishing the formula that would be used when determining volumes of spheres and cylinders. He went ahead to discuss properties of Archimedean spiral that he described as being the distance from a point that is fixed for instance 0 of any point, say P on the spiral, is normally proportional to the angle that is located between OP and another fixed line O. Through this evaluation of areas that he made that involved the spiral he paved way for the development of calculus that was put to a book in the seventeenth century (Ferris, 2010).
In order to complete the Pizza Box problem, students must have great calculus and pre-calculus knowledge. Anyone who wants to do pre-calculus and calculus would definitely do it successfully depending on the previous foundation in mathematics that incorporates the basic information required. A learner should not just forget the fundamentals of Calculus immediately after a test or examination as this might position a student behind most of the time. It is always important to make sense of whatever the students learn particularly in mathematics. The primary building blocks of mathematical literacy include understanding times-tables or basic arithmetic facts that serve as the core for nearly all mathematics learning that follows afterward. However, rote learning does not link properly with the current digital technology, which has made learning easier by doing grunt work for learners. This form of writing presents some pros and cons of learning to work pre-calculus and Calculus problems by hand.
According to “Classroom Professor”, it is undeniable that arithmetic begins from a particular foundation, which includes principles for the numeration system, operators, symbolic system, and all other basic information. Utilization of the basic calculus thought remains vital for students. A number of people believe in the mathematical concept and therefore using the manual process of teaching calculus ideas will result in massive universal support. According to Orlin (2013), most of all, they complain that rote learning has become taboo, rather than accepted as a healthy part of a balanced scholastic diet.
It is essential to understand that manual learning of using pre-calculus and calculus by hand improves focus mental attention, focus to detail, and is free from distractions, thus making it an exceptional mental workout. Understanding basic ideas and arithmetical principles can never be substituted with digital technology since the brain is more superior to the technology unless a learner has learning or mental disability. Students who do not understand the fundamental concepts of Calculus may hardly understand numerous related topics or basic arithmetical concepts that were crucial in the primary mathematics curriculum. Mental computational abilities tend to eliminate issues of struggling to reach an understanding of concepts the learners could have learned in lower grades.
This report has shown the need and importance of calculus and mathematical problems in solving complex real-life problems. The Pizza Box problem applies calculus in solving a seemingly complex packaging problem. The cost reduction and material optimization that is achieved through calculus-inspired design is a true testimony of the power of mathematics in solving real-life problems. Every student must, therefore, take their calculus and pre-calculus lessons seriously since they hold solutions to some of the world’s common problems.
References
Daley, T., Gutierrez, M, & Wilkerson, M. (2015). Pizza Hut Project. Web.
Delfour, M. C., & Zolésio, J. P. (2001). Shapes and geometries: Analysis, differential calculus, and optimization. Philadelphia, PA: Society for Industrial and Applied Mathematics.
Dundas, K (1984). To Build a Better Box. The College Mathematics Journal, 15(1) 30- 36.
Electric Teaching. (2013).Calculus – Optimization Open-Top Box Max Volume. Web.
Eley, M. (2002). Solving container loading problems by block arrangement. European Journal of Operational Research, 141(2), 393-409.
Ferris, D. (2010). The Contributions of Archimedes in Geometry. Web.
Films Media Group & KM Media. (2015). Dimensions that Maximize the Volume of a Box: Calculus-Applications of Derivatives: Applied Optimization.
Optimization Problem – Max Volume of a Box Made From Square of Material. (2011). Web.
Orlin, B. (2013). When Memorization Gets in the Way of Learning. Web.
Pisinger. (2002). Heuristics for the container loading problem. European Journal of Operational Research, 141(2), 382-392.