Introduction
Traditional supply chain system models deal separately with just two factors, which are the location, “the site of the facility”, and inventory management. Also, due to poor estimates and uncertainty, the parameters of those factors used to be inaccurate and gave erroneous results. However, the advanced supply chain systems have promoted the supply chain network regarding reliability and efficiency. In reality, globalization and outsourcing of supply chains increase business risks and uncertainty during manufacturing operations or any associated processes (Barry, 2004; Christopher et al., 2011; Waters, 2011) because the future operations, processes, conditions, and activities of an SCS are largely unknown (Klibi et al., 2010). All these serious factors increase the need for designing and optimizing SCS. Also, keeping on competition and maintaining the market drove companies to be more concerned about optimizing their systems. Applying the reliability concepts and effectively optimizing systems to be more reliable is a key to having a robust SCS. A robust technique was first introduced by Taguchi (Hwang et al., 2001; Taguchi, 1987; Taguchi & Phadke, 1988). The Taguchi technique helps to find a robust solution that is less sensitive to unknown variations.
Moreover, this paper introduces an approach that is effective in measuring and optimizing the supply chain system by implementing the reliability concept, which is associated with the cost that needs to be minimized particularly in global SCS. Costs are incurred from the start of moving materials throughout such a global supply chain; therefore, the costs are incurred along the entire end-to-end chain. In other words, the costs are experienced from the supplier’s supplier to the customer’s customer. These basic principles drive the identification of global supply chain costing. Along with that, managers who are highly responsible for the effectiveness and efficiency of global supply chain systems need to show performance indications that are timely, accurate, complete, effective, and actionable. Therefore, global supply chain costing starts with the essential objective of gaining high SCS performance. Also, measuring the performance is a primary step to evaluate the reliability of a supply chain system. The use of reliability theory as a performance measure for supply chains is one of the main purposes of this contribution, which includes the consideration of uncertainties to improve the supply chain’s reliability.
Furthermore, outstanding time performance for entities in the supply chain should be weighed against the corresponding costs. In fact, as mentioned by So (2000), it can be costly to deliver outstanding time performance when time delivery performance depends on the operating efficiency of the system and the available capacity. It is obvious evidence that in the situation of time-sensitive products, with different characteristics of different products being an example, an appropriate method of managing the supply chain for such products must be concerned about both the operational (and other) costs, as well as the time factor. Therefore, companies need to improve the adequacy of their delivery systems to achieve the desired time performance by having a minimum cost of operating.
In general, reliability is defined as an item’s ability to start and continue to operate (Modarres, Kaminskiy, & Krivtsov, 2009). The SCS model gives a mathematical approach that can be followed to enhance the reliability rate of the system by having minimum total costs of having processes done. Many studies are aimed at systematically treating uncertainties in engineering analysis and, more recently, developing RDO (Chen, Hasselman, & Neill, 1997; Choi & Du, 2005; Du, & Chen, 2004; Youn & Wang, 2009; Youn, Wang, Hu, & Youn, 2011; Wang, Wang, & Almaktoom, 2014). The SCS approach characterizes uncertainty variables and failure modes to optimize the designs and gain a high-reliability indication. This paper concentrates on developing a reliability design optimization model that seeks to fulfill the reliability requirements in every stage of the SCS while overcoming the uncertainty and minimizing the overall cost. Also, the suggested model will make a balance between reliability requirements and cost.
An optimization model for reliability in the supply chain system
The optimization algorithm is designed to optimize the reliability of the supply chain system. The objective function of the model is to minimize the delay that happens in specific jobs as a result of a preceding entity or job and variability between system entities. While some constraints are required in the objective function, the reliability rate for each component and the overall system are required too. In this thesis, the objective functions of all the components are assumed to be evenly significant. However, cases are different from field to field; therefore, different weightings for objective functions of components will be addressed. Many scholars have given assurance that multiple objectives can be gathered into one objective function by considering the weighted sum of all functions (Deb, 2001; Konak et al., 2006; Murata et al., 1996; Yildirim & Mouzon, 2012). The weight can be addressed on the objective function, depending on the importance of the entity.
Equation (1), Equation (2)
Where σ X(i,j) is the standard deviation, which is the delay caused by the internal uncertainty of entity type X number i in level number j. Here, εX(i,j) is the delay function of entity type X number i in level number j , which entity spent waiting for materials or parts from the preceding entity type X number i in level number j-1). Also, ωn represents the weight assigned by decision-maker. It is obvious that ΩX(ij) stands for the reliability rate function of the ith entity type X at level j and ΩTX(ij) is the required (target) reliability rate for the ith entity Type X at level j. The mean time for finishing the required task at entity type X number i at level number j is represented by µX(i, j). Also, µ u i, j and µ lX(i,j) are the upper limit and lower limit of the X(i,j) design variable respectively. Eventually, TT symbolizes the system total desired (target) cycle time and X symbolize the type of entity or component, which can be a supplier (S), factory (F), or route (R).
Case Study
This case study illustrates a company that has a supply chain system that includes four phases and seven entities. These entities, which are connected in series, form the system, which consists of the following components with their values as provided in the table below:
Table 1. Means and Standard Deviations for the System Components
The cost of each entity is stated in the table above. The objective of this case study is to test the measurement of the system reliability and identify the optimal cost of the system utilizing the developed model. Also, the aim is to demonstrate the efficiency of the performed methodology for assessing and optimizing the reliability of each entity in the system, as well as the overall system. The other objective is to figure out the minimum cost of moving parts or products through the supply chain system. The target reliability rate of the case study is to reach at least 95% at the minimum cost.
Results
First of all, the SCS mathematical approach was utilized to evaluate the current system performance using equation (1). After collecting data and applying the suggested model, it has been concluded that the initial cycle time of having one batch done is 615 hours, and the initial reliability rate of the system is steady at 73.17% (see Table 2). Also, the initial delay reached 165 days, which meant that when a retailer made a request for a batch of products, it would take 615 hours and record 165 hours as the delay. Hence, applying the optimization model is necessary to achieve the reliability requirements while taking the minimum cost into consideration.
Table 2. Initial Figure of the SCS
The results of the case study were achieved as shown in the table below by implementing the developed optimization model equation (2). Table (3) shows the initial mean time at each entity, as well as the optimal mean time. For example, the supplier’s initial mean time reached to 94, whereas the optimal mean time for the same entity recorded minimum value, which was steady at 80 hours.
Table 3. Comparison between Initial Mean Cycle Time and Optimal Mean Cycle Time
Moreover, the required cycle time was obtained, and the SCS delay was minimized by applying the same optimization model. From Table (4), while the initial cycle time of delivering one batch was 615 hours, it is obvious that SCS with optimization model decreased to 475 hours per batch after repeating many times to ensure the optimal points were reached. The delay recorded just 25 hours per batch. Also, the reliability rate increased to reach the optimal rate at 95.36%. From the same table, it is clear that the total cost of having the batch done was minimized to achieve the optimal cost, which was $182,250. Hence, all constraints and requirements, such as the overall SCS reliability rate and the optimal total cost, were satisfied.
Table 4. Optimal Cycle Time, Delay, and Reliability Rate
Table (4) shows the optimal figures after implementing the model.
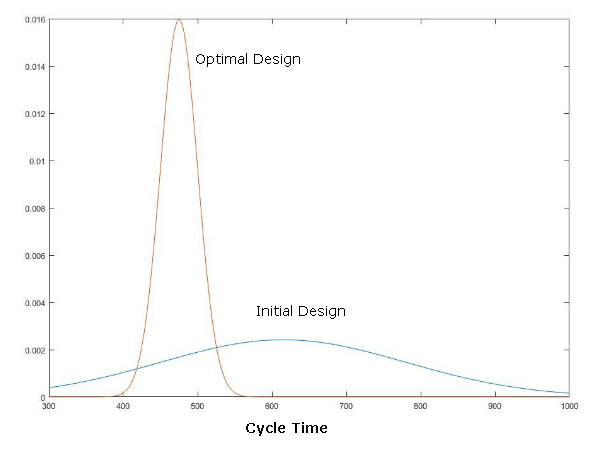
Figure 1 illustrates the comparison between the initial function and final probability density functions of the system. By comparing distributions of the total cycle time of initial and optimal SCS design, it was clear that the time variation was significantly decreased due to the reduction in the total delay of the system. The optimization model achieved lower mean cycle time, which reached around 475 hours, whereas the initial mean cycle time of the SCS was around 615 hours. Regarding the comparison between the initial system design and optimal system design, the developed system design had lesser delays of delivering batch, as well as less cycle time which fulfilled the reliability requirements and the profitability.
Conclusion and Future Work
There is always need to improve the reliability concept in supply chain system as more companies, departments, organizations, and other divisions are being involved in the supply chain’s structure. Also, from a business perspective, minimizing costs is a significant matter that has to be addressed to have reliable and robust SCS. This research has concentrated on evaluating reliability rates at each entity through the SCS. Also, this paper explains how the SCS optimization model could be applied to reduce the total cost while fulfilling the reliability requirements. The effects of uncertainty driven by production and transportation on overall reliability were examined in the paper as well. In conclusion, the optimization approach that has been presented in this study is to provide an appropriate method that helps to satisfy the reliability requirement at the minimum possible cost. As a future study, this study will continue to investigate how reliability performance influences the total cost of managing each step in the supply chain, as well as for the overall SCS.


