The decision-making can be an extremely complex process in multiple situations. This is especially the case when the outcomes will have far-reaching consequences for someone’s life and well-being. The following paper will address the process of the decision-making based on the case of Mrs. Jones, who was offered the bypass operation due to her defective heart valve problem. Overall, the application of the decision table model and decision tree suggests that the best alternative for Mrs. Jones is to agree with the heart surgery because her chances to survive longer are much higher in this case.
The decision-making process based on the offered case should be guided by the theoretic framework, which is the decision table and decision tree (Kerzner 75; Kotler 22). The theoretic resources state that adoption of the best decision in each particular situation requires a deep analysis of the existing problem, finding all possible alternatives, identifying the expected outcomes, selecting the applicable decision model, and actually choosing the best alternative (Bourne 7; Segatto and Dante 714). These essential components apply to every decision-making graphic model whether it is the decision table or decision tree (Bowen and Murshid 223).
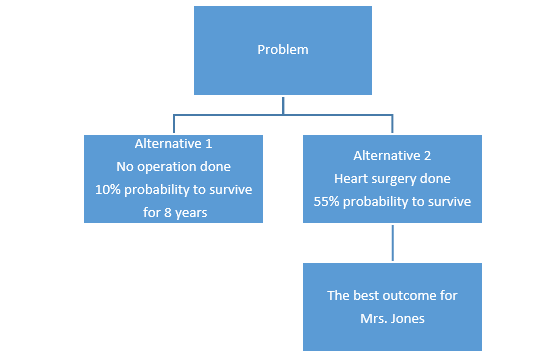
According to the decision tree model, the process of the decision-making in this situation will include such steps as evaluation of outcomes for every alternative and selecting the alternative with the best output (Segatto and Dante 713; Vermeulen and Pyka 2). Implementation of this theoretic information to Mrs. Jones’ case suggests that the first alternative which is the refusal to make an intervention has a poorer outcome for the person than the decision to have the bypass operation. The probability of surviving is higher if the person chooses alternative two. Therefore, the ultimate decision for Mrs. Jones is to agree with the medical doctor’s offer to undergo heart surgery.
The same conclusion can be made based on the usage of the decision table:
Fig. 2. Decision table.
This model will also demonstrate that the alternative with the best outcome for Mrs. Jones’ is the resolution to agree to the physician’s offer.
Other Factors that Need to Be Considered
Mrs. Jones’ situation overview has identified the following risks: (1) failure to do the heart surgery results in only 50% chance to survive for one year, 20% chance to survive for two years, and 10% to live 8 years more; (2) 5% of patients do not survive the bypass operation or die during the recovery stage and 45% do not survive the first year; (3) at any development, the physician admits that surviving after the age of 58 is very low. With these striking data, Mrs. Jones needs to approach the decision-making process extremely seriously.
Concluding on the information mentioned above, the decision-making process requires the systemic approach to take into consideration all the factors that apply to the situation along with the possible threats and risks. The best decision is the decision of choosing the alternative with the optimal outcome. Application of this theoretic information to the given case study suggests that Mrs. Jones should choose to do the surgery because this alternative has the best outcomes for her. This conclusion can be made either with the use of the decision table or the decision tree.
Works Cited
Bourne, Liam. Stakeholder Relationship Management, Farnham, GB: Gower, 2012. Print.
Bowen, Elizabeth and Nadine Shaanta Murshid. “Trauma-Informed Social Policy: A Conceptual Framework for Policy Analysis and Advocacy.” American Journal of Public Health 106.2 (2016): 223-9. Print.
Kerzner, Harry. Project Management – Best Practices: Achieving Global Excellence, Somerset, NJ: John Wiley & Sons, Incorporated, 2014. Print.
Kotler, Peter. Marketing Management, Upper Saddle River, NJ: Prentice-Hall, 2011. Print.
Segatto, Mayara and Pinheiro Martinelli Dante. “Business Process Management: A Systemic Approach?” Business Process Management Journal 19.4 (2013): 698-714. Print.
Vermeulen, Ben and Andreas Pyka. “Agent-Based Modeling for Decision Making in Economics Under Uncertainty.” Economics 10.6 (2016): 1-33A. Print.