Introduction
For the academic community of past centuries, it was common not to listen to women’s views and keep them out of scientific work. For a long time, it was thought that women could not bring new knowledge to science, and therefore their presence in universities and laboratories was undesirable. However, the history of the world has consistently sought to show otherwise: Ada Lovelace, Marie Curie, Wu Jianxiong, and hundreds of other women from around the globe have contributed to specific fields of knowledge comparable to men. One of the most striking examples of gender bias in academia is the story of the French female mathematician Sophie Germain, who made significant contributions to differential geometry and number theory. This essay evaluates this contribution and describes the significance of Germain’s figure for the mathematical sciences.
Main body
Primarily, it would be helpful to briefly discuss the biographical details of Sophie Germain’s life, without which a study of her academic weight is incomplete. Sophie was the child of a liberal jeweler who disapproved of his daughter’s pursuit of mathematics (Flanders, 2018). The girl’s parents can be understood: society did not recognize a woman’s intellectual capacity, so an earlier investment in a child’s development of scientific knowledge might have been ultimately detrimental. Nevertheless, Sophie used her father’s library and studied math books on her own, one of which was Montucla’s “History of Mathematics” (Swetz, 2017).
Growing up, Sophie was aware that she would not make meaningful progress in science because of her gender, so the woman had to adopt a male pseudonym: Sophie began using the name Monsieur Leblanc (Flanders, 2018). Sophie used this name in her business correspondence with the eminent mathematicians of the time, namely Dalembert, Lagrange, Fourier, and Gauss. Her secret was soon discovered, but it was followed by public recognition and landmark awards. Thus Sophie always used the opportunities and tricks available to her to do herself, which ultimately allowed the woman to solve one of the most critical problems in mathematics.
One of the fundamental theorems of algebra is called Fermat’s Last Theorem. This statement postulates that equations of the form
an+bn=cn — a particular case of which is the Pythagorean theorem for right triangles — where n>2 have no solutions in the numbers a, b and c. Many men of science have tried to prove this theorem, which is a challenging task, especially for the level of proficiency in mathematics characteristic of the nineteenth century. Sophie Germain created a proof of this theorem for several exceptional cases — for example, when n=5 — which was an impossible task for Euler and Gauss (Flanders, 2018). The universality of the proposed solution made it possible to noticeably expand the range of prime numbers for which the theorem worked since Germain proved the effectiveness of the Last Theorem for all prime numbers smaller than a hundred. In other words, unlike redundant but unworkable proposals by other mathematicians, Sophie did not focus on private proofs but instead found a solution for a whole class of numbers when n=8k+6.
Among Germain’s mathematical discoveries, her proposed number theorem should be highlighted, which, although correct, has not received adequate attention from the academic community. In general, the problem she constructed was to prove that a number of the form a4+4 was not prime. The elegance and wit of her solution to this problem cannot fail to amaze. In the equation below is the approach by which Germain proved the complexity of this number. In this solution, one sees that if a4+4 can finally be represented as the product of two multipliers, then it is a composite.
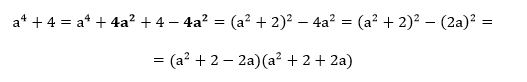
Another of Germain’s apparent contributions to science was the study of elasticity theory using Chladni plates as an example. As a German physicist in the field of acoustics, Chladni discovered that sand poured on thin plates takes on a spectacular pattern when vibrations are applied to them (Lydon, 2018). Napoleon instituted a two-year competition and a significant prize for whoever could theorize the phenomenon. Germain spent two years studying elasticity theory, analytical mechanics, and vibration theory, but she lacked the depth of physical knowledge to complete the work. In the meantime, her work was improved upon by Lagrange, resulting in a solution to the Chladni problem for several simple cases.
This included Germain’s severe criticism of Poisson’s academically accepted approach to solving the problem, although according to modern concepts of acoustic physics, Poisson was not wholly accurate (Adeoye & Awodola, 2020). Eventually, and after numerous attempts to clarify her proofs, Sophie Germain was awarded the Napoleonic prize, but she defiantly did not show up at the award ceremony.
Conclusion
In conclusion, it should be emphasized that the scientific communities of past centuries were not as loyal to women as they are today. Because of this, there are few examples of women who have truly revolutionized the sciences. Sophie Germain is one of them: raised in an environment of non-recognition of her mathematical abilities, Germain was forced to hide behind a male pseudonym in order to correspond with iconic French mathematicians. Sophie was able to provide proof of Fermat’s Last Theorem for a whole class of prime numbers, develop her own proof of the complexity of any number of the form a4+4, and create a foundation for solving the Chladni problem for the elastic vibrations of sand on plates. It is safe to say that Germain was in many ways ahead of her time, and had she been born later, her intellectual contribution to mathematics would have been even broader.
References
Adeoye, A. S., & Awodola, T. O. (2020). Dynamic Behavior of moving distributed masses of orthotropic rectangular plate with clamped-clamped boundary conditions resting on a constant elastic bi-parametric foundation. International Journal of Chemistry, Mathematics and Physics, 4, 71-91. Web.
Flanders, K. (2018). Sophie Germain and the struggles of women mathematicians during the French revolution [PDF document]. Web.
Lydon, S. P. (2018). Signatura rerum: Chladni’s sound figures in schelling, August Schlegel, and Brentano. The Germanic Review: Literature, Culture, Theory, 93(4), 334–350. Web.
Swetz, F. J. (2017). Mathematical treasure: Montucla’s history of mathematics. MAA. Web.