A big idea is a concept or statement that is core to the study of mathematics. It connects various topics in the mathematics syllabus into one big idea. The concept of big ideas focuses on breaking down the mathematics curriculum into subsections that can be taught and learnt easily. The advantages can be assessed in two perspectives in terms of the importance to the student and teacher because the big ideas concept focuses on making learning and instructions easy and understandable (Australian Curriculum, Assessment and Reporting Authority, 2014).
One of the major advantages that a student enjoys from this concept of learning mathematics is the connection between new and known ideas being learnt. At a higher level of learning, students learn about fractions which are just a continuation of the learning sections which started at pre-school (Charles, 2005).
Big idea’s help students relate what was taught in the first year to the subsequent ones. This aspect has high importance because it makes learning fast for the student (Knowing and Learning Mathematics, 2001). Secondly, the learner benefits from the big ideas focus by being provided with the opportunity to explore concepts thoroughly. Ontario Education (2006) stated that programs that are organised around big ideas provide cohesive learning opportunities that will allow students to explore mathematical concepts in depth. This allows students to embrace the conceptual foundations of mathematics.
Apart from being an advantage to the learners, Charles (as cited by Siemon, Bleckly and Neal, 2012) claims that focusing on big ideas and the links between helps to deepen teacher knowledge and confidence for teaching maths. Another advantage of the big ideas to the teacher is categorization of topics. Categorization of topics is very useful as it will assist the teacher when teaching mathematics using connected ideologies. The related topics of study are taught in a connected way according to the concepts of big ideas (Van-de-Walle, Karp, & Bay-Williams, 2013). Big ideas can make selecting instructional decisions and identifying prior learning easier.
Chosen Big Idea: Numbers
Numbers are the baseline and determinants of the perspectives in mathematics. Being able to understand and work with numbers is essential in every aspect of everyday life. Understanding numbers means being able to estimate, measure, calculate mentally, to compute using different ways and use calculators when necessary. Furthermore, understanding numbers is important for students to be able to make sense of a problem as well as making sense of solutions (Booker, Bond, Sparrow and Swan, 2010). A great sense of numbers helps student’s make sense of the world around them.
To simplify numbers, they can be classified into whole, counting or integers. The practise of counting identifies the tally of thing available at an instance. Primarily, the final number of a tally identifies the amount of items or things present. The items presented in a group are represented by a specific symbol and word. Each symbol is a representation of integers. There are many points between integers in a number line. The lowest integer is zero while the lower counting number is 1. The whole numbers are related strictly to certain point of a number line. These numbers help in identifying the positions of items by the use of position like second and third. These key understandings form the basis of the ‘Big Ideas’ of numbers.
Quantity, operational sense, relationships and representations are all Big Ideas of numbers that students must learn to be successful in all other areas of maths. Firstly, the big idea of quantity is identifying how much there is of something. Having an understanding of quantities represented by whole numbers, decimal numbers, fractions, and percents is the foundation of all mathematics (Ontario Education, 2006).
Quantity
Quantifying numbers is an imperative aspect in order to understand their values. This practise commences within the primary grades where learners are introduced into the value of 2-3 digit numbers (Smith & Adams, 2009). For instance, students are taught to compare values of these numbers using such phrases as ‘more than’, ‘less than’, and ‘equals’ among others. A step further, the junior grades are made conversant with quantification of multi-digits including the percents, decimals, fractions and integers. The instructions are aided by such enhancements as picture and practical involvement of learners especially in instilling the concept of fractions and their values.
The most paramount techniques of enlightening learners of the junior grade on value of whole numbers involve the use of place values. For example, the number 4967 has 4 thousands, 9 hundreds, 6 tens, and 7 ones that quantifies that strength of each digit in the number. When students learn that the place values exceed by a multiple of 10, the meaning of each digit becomes elaborate. The decimals apply a similar concept where each digit is associated with the place values for quantification. However, quantifying fractions is related to its closeness with zero. In junior grades, these basic values are preceded by the meaningful quantification involving distances, mass, weight, temperature, and time among others.
Operational Sense
Knowing and valuing numbers is practically essential, but sensibly too basic for the numbers operations. Students of the primary grades are introduced to concepts of addition and subtraction where they count, combine, and partition numbers (Tainsh, 2002). Their subtraction and addition habits make meanings for multiplication and subtraction. This understanding is attributed to use of repeated addition and subtraction of equal parts. However, the actual multiplication techniques kick in the junior level where an understanding of grouping starts (The Oxford University Press, 2014). Furthermore, the learning is reinforced by rules and principles. For instance, any number multiplied by zero gives an answer 0. Adding a number repeatedly from zero gives the multiples of that number.
Relationships
Relating numbers and developing a sense of their sequences assists students to establish solid connections in mathematics. The relations enable a strong adherence to the number system as well as its operations (Tainsh, 2002). In the junior grades, the learners get a basis of identifying why some fractions are lower of higher than others. For instance, 3/10 is greater than 1/5 since 1/5 is equal to 2/10. This enlightenment makes it easy to compute using numbers. All the four operations of adding and subtracting introduced in the primary grades are applied for junior grades while involving huger numbers. The relations of fractions, numbers, percents, and fractions are also met here at the junior level. For instance, 17% is equal to 17/100 and 0.17.
Representation
Numbers can be represented in various ways for simpler understanding and recognition of their value. For instance, 169 can be represented by 132. On the other hand, the huge figures like 6000000 can be represented as 6 millions. The other one is about ratio that involves the use of a sign ‘:’. For instance, 2:3 may imply 2 for every 3 things. These strategies make the reading of numbers and their writing easier and not confusing. The placement of digits and their values acts as quantifiers (Siemon, Bleckly, and Neal, 2012). For instance, when considering 6 in 760 and 560000, the first represents 6 tens while the second is 6 ten thousands. However, a clear understanding is imperative for distinction between whole numbers and decimals. The decimal point represents the separation. For fractions, teachers provide many concrete models to elaborate the fraction concept.
Concept Map
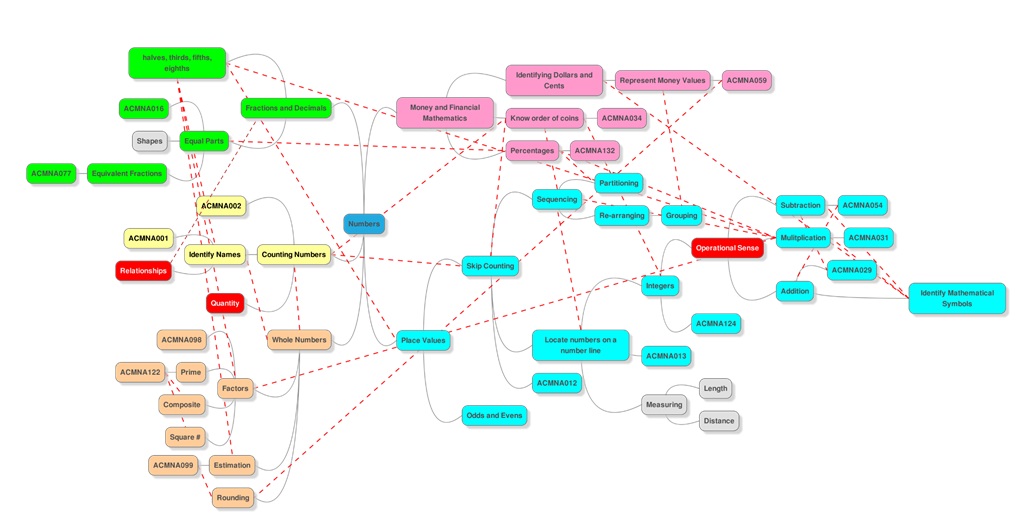
Note: All codes taken from ACARA (Australian Curriculum and Reporting Agency), 2014.
Curriculum Links
References
Australian Curriculum, Assessment and Reporting Authority. (2014). Web.
Charles, R. I. (2005). Big Ideas and Understandings as the Foundations for School Mathematics. APS Mathematics Teacher 6(2), 1-6.
Knowing and Learning Mathematics for Teaching: Proceedings of a Workshop (2001). The National Academies Press,12, 6.
Nelson, T. (2002). Mathematics Education: A Summary of Research, Theories, and Practice. New York: Oxford.
Siemon,D., Bleckly, J. and Neal, D. (2012). Working with the Big Ideas in Number and the Australian Curriculum: Mathematics. Web.
Smith, D., & Adams, S. (2009). If…: A mind-bending new way of looking at big ideas and numbers. New York: St. Martin’s Press.
Tainsh, R. (2002). Numbers. New York: Priddy Bicknell/St. Martin’s Press.
The Oxford University Press. (2014). Web.
Van-de-Walle, J. A., Karp, K. S., & Bay-Williams, J. M. (2013). Elementary and Middle School Mathematics: Teaching Developmentally. New York: Pearson.