Temperature Effects in Laser Diodes Report

Introduction

Laser diodes in the context of changing characteristics at different temperatures require an integrated approach based on technological and mathematical models. These approaches are conditioned by a unique set of properties that contribute to the mass of application possibilities of these devices. Pretty often, implementation should be accompanied by at least a minimal preliminary calculation based on models that take into account mathematical, physical, and chemical interactions. Technological processes provide empirical data that can later be used with a predictive function. The issues of thermal conditions are often raised in the latest applied problems, requiring such a high accuracy of calculations in various spectra of external temperatures. As a consequence, the implementation in the scientific and industrial fields places new and higher demands on these devices, which require a more comprehensive assessment.

Studying radiation parameters has a multicriteria structure, especially concerning the search for their correlation with temperature changes. Semiconductor lasers in applied fields of science are used quite often, and therefore, their study is relevant to current conditions. For example, these lasers have an extensive radiation range, are compact, have a low operating current and low operating costs while being highly efficient, and are used almost everywhere, from science to medicine. It is one of the broadest classes of laser sources. This work describes the radiation characteristics of laser diodes in a semiconductor for the different temperature values. As a result, conclusions are drawn about the main characteristics of the laser, which depend on temperature, according to the presented studies.

Temperature Impact

In semiconductor lasers, the optical emission spectrum is formed due to interband transitions, or “zone-by-zone” transitions, from states at the lower edge of the conduction band to conditions at the upper edge of the valence band. Moreover, exciton transitions are distinguished during the recombination of an electron and a hole bound into a neutral mobile formation of an exciton, or transitions “zone-small impurity,” which refers to a local center that has an energy level split off from one of the allowed zones by a small energy distance compared to the bandgap (Diaz et al. 1043). Thus, the wavelength λ of radiation from a semiconductor laser is related to the bandgap E_g by the relation, where h is Planck’s constant and c is the speed of light in vacuum

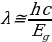
This ratio will be defined in the text as the first one. Injection lasers use an efficient way to obtain excess electrons and holes – their injection through a nonlinear electrical contact, for example, a p-n junction. The carrier injection mechanism through a p-n intersection is based on the diffusion of carriers from a region with a higher concentration of pages to an area with a lower concentration (Diaz et al. 1044). It can be shown that to obtain an inversion on transitions of pages with photon energy hc/λ using electric pumping, and a voltage V must be applied to the active element of the laser, satisfying the condition, where is the electron charge

This condition will be defined in the text as a stress condition. Numerical evaluation of the voltage required to create an inversion for a laser with a wavelength of 635 nm, following the voltage condition, gives a voltage value of more than 1.96 V (Sato et al. 15). If radiation with a wavelength of 610 nm is considered, then the voltage required to create an inversion should be more than 2.0 V. It follows from the first relation that the radiation wavelength, within an accuracy of 2–3%, is determined by the bandgap of the semiconductor-based on which the laser diode is made. Consequently, the emission wavelength of a semiconductor laser diode is described by a temperature dependence similar to the bandgap in the same linear order (Sato et al. 20). Experimental estimates of the temperature coefficient of change in the bandgap β for several semiconductors, taken from various literature sources:

In this equation are bandgaps in temperatures and respectively. In several works, it is noted that the mode composition of the radiation of a laser diode can change significantly with changes in operating conditions. It was also found that only pulsed measurements, excluding crystal heating, make it possible to reliably estimate the quantum yield of the LED structure and its change with current density. Although this study relates to LEDs, its conclusions, to a certain extent, should be taken into account when working with laser diodes (Sato et al. 14). The interband transition has a direct proportional relationship with the radiation wavelength, then, according to the operational data of the laser diode, one can approximately obtain an estimate of the change in the band gap in the following relation.

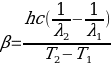
In this equation, is the laser wavelength corresponding to the temperature , while index 2 shows similar maximum values. It is obvious that the power emitted by the laser is determined not only by the amount of input power, but also by the efficiency of the emitter. Depending on the latter, the difference between the input and radiated power is spent on heating the volume of the semiconductor structure of the laser, which can lead to a change in the wavelength of its radiation. An analysis of the factors that can affect the wavelength of a semiconductor laser with a change in its operating temperature shows that the main factor is the effect of temperature on the band gap of the semiconductor from which the laser is made. The chemical and physical processes in the semiconductor material begin to show up significantly in relation to the band gap relative to temperature in the range from 125 to 155 K. In this case, the value of the temperature coefficient of change in the band gap β changes from (–2.38 ⋅ 10^–4) to (–4.62 ⋅ 10^–4) eV/K (Sato et al. 24). At the same time, specifically in this study, they resorted exclusively to low temperatures.

Similar work raises the issue of modality of the temperature spectrum and proposes a multimode sector model, as shown in Figure 1. Figure 2 shows the change in the emission spectrum, while temperature is plotted on the other axis. Stimulated emission exhibits a spontaneous character in the range just above 265 K, while partially stimulated emission is also included in the operating values, as a rule, presented in the passport data of the laser used.

These images demonstrate that only specific wavelength parameters can guarantee the emission of a laser diode at any temperature. For the further description of this study, the wavelength will be considered equal to the maximum radiation intensity in the considered context of the temperature value. For the L1 laser, on the plot of the Eg(T) dependence, two sections can be distinguished with different values ​​of the exponent β: the first one is in the temperature section from 50 to 130 K, the second one is in the section from 150 to 270 K in figure 3, curve 1 (Deng et al. 45). The value of the temperature coefficient of change in the band gap width is β = –2.38 × 10^–4 eV/K for the low-temperature region and β = –4.62 × 10^–4 eV/K for the high-temperature region.

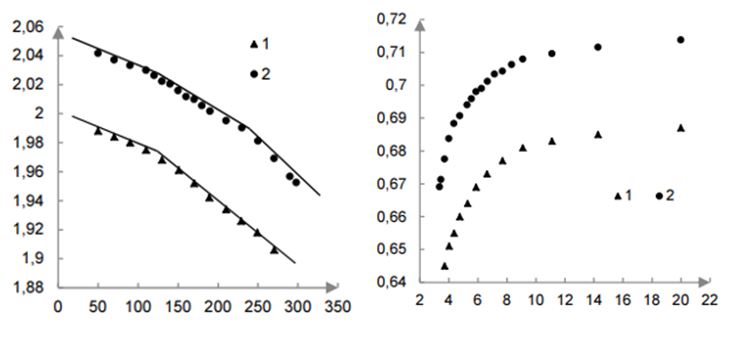
For the L2 laser, the dependence Eg(T) can be divided into three temperature intervals, which correspond to different values of the coefficient β: the first is from 50 to 130 K, the second is from 130 to 250 K, and the third is from 250 to 300 K in figure 3, curve 2. Coefficient β = –2.04*10^–4 eV/K for the first low temperature section (Deng et al. 48). In the second average temperature range section β = –3.2*10^–4 eV/K. In the third high-temperature section, β = –6.5 10^–4 eV/K.

The thermal expansion of the lattice based on the direct relationship between the cell volume and the number of energy levels of charge carriers, including the electron-phonon interaction, has a cumulative effect, which manifests itself through temperature on the crystal structure by zones. It is assumed that the dependence on one lnE_g(1/T) analysis would allow us to determine the activation energy of the processes that affect the change in the bandgap. Indeed, plotting the dependences of the natural logarithm of the bandgap lnE_g on the reciprocal temperature in figures 3 on a stretched scale made it possible to accurately determine the activation energy E_i of the processes that affect the change in the bandgap (Deng et al. 49). The activation energy E_i in a specific temperature range was determined from the relation

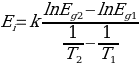
In this equation E_g1-2 is bandgap corresponding to the beginning and the end of the temperature interval respectively, k – Boltzmann constant. The recombination of an electron and such a parameter as a gap in a p-n junction form the basis of the emission of the considered diode. The described processes occur when the movement of an electron lies in the region of the valence bands, and not in the conduction bands, which leads to an interaction with a gap (Straker et al. 20). However, in some cases, the process of direct recombination can be replaced by the formation of an exciton, which is subsequently annihilated, emitting a light quantum with an energy much less than the band gap. At the same time, destruction of the extion may not occur for a long time, which will in no way affect the radiation. A similar phenomenon often occurs under certain conditions, for example, at temperatures above 80 K, most of the radiation is formed by extons (Straker et al. 19). Impurities in certain compounds of type A(III) or B(V) can also form radiation based on exciton annihilation if the crystal lattice is imperfect.

The activation energy E_i obtained in the experiment represents exactly quantity describing the ionization energy in the region of the conduction band, including exciton level. The Wannier-Mott exciton energy spectrum formula gives the exciton energy without considering the motion of its center of mass (Balci et al. 169). The zonal differentiation of the excition spectrum is determined by the inclusion of displacement and motion of the particle’s center of mass (Balci et al. 170). Moreover, it can explain that in the temperature ranges of 230–190 K and 190–170 K, relative values ​​of the ionization energy of the exciton level are observed: 0.533 meV and 0.565 meV. Perhaps these energies correspond to the same value of n, equal to 10, as shown on the next correlation.

Conclusion

In the temperature range of 50–300 K, processes occur in the semiconductor material from which the laser diode is made, leading to a change in the bandgap by approximately 4.5%. The dependence E_g(T) can be divided into two or three temperature intervals corresponding to different values ​​of the temperature coefficient change in the bandgap. This coefficient in the temperature range of 50–300 K can vary in absolute value by a factor of 2–3. The value of the bandgap in the temperature range of 50–300 K can vary by 4.2–4.5% of the value corresponding to a temperature of 50 K. making it possible to use a laser diode as an instrument with a very narrow spectral emission line of sufficiently high intensity. A similar dependence can also be observed in terms of activation energy and current thresholds.

Works Cited

Balci, Mustafa H., et al. “Comparative study of blue laser diode driven cerium-doped single crystal phosphors in application of high-power lighting and display technologies.”Optical Review, vol. 25, no. 1, 2018: 166-174. Web.

Deng, Zeng, et al. “Temperature distribution and thermal resistance analysis of high-power laser diode arrays.”International Journal of Heat and Mass Transfer, vol. 134, 2019: 41-50. Web.

Diaz, Joseph, et al. “High-Temperature Reliability of Aluminium-free 980 nm and 808 nm Laser diodes.” Compound Semiconductors. CRC Press, 2020: 1041-1046.

Sato, Kosuke, et al. “Room-temperature operation of AlGaN ultraviolet-B laser diode at 298 nm on lattice-relaxed Al0. 6Ga0. 4N/AlN/sapphire.” Applied Physics Express, vol. 13, no. 3, 2020: 2-33. Web.

Straker, Michael, et al. “Growth of high purity zone-refined Boron Carbide single crystals by Laser Diode Floating Zone method.”Journal of Crystal Growth, vol. 543, 2020: 1-25. Web.