The Concept of the Derivative of a Function Coursework

Define the concept of the limit of a function using the formal delta-epsilon definition

The limit of a function is a very important concept in mathematical expressions. In mathematics, every function behaves in a certain way with respect to changes in input. For instance, a function moves towards a certain set value as input also moves towards a target value. This is the concept of a limit. A limit is that set value that a function gets closer to as its input moves towards a target value (Stewart, 2008). Simply, limits are mathematically precise ways of representing how a function acts when its independent variable is close to a certain number. Limits are used to define integrals, continuity, and derivatives in calculus. Mathematically, limits are used to analyze the behavior of a function f with reference to a particular input x. Therefore, f(x) is a mathematical output of f with reference to an input x.

The function has a limit L at an input p if f(x) is “close” to L whenever x is “close” to p (Stewart, 2008). The concept of “closeness”, i.e., is well-defined using the delta-epsilon definition of a limit. The above statement would then be restated as: function f(x) has a limit L if f(x) is within epsilon (ε) values of L whenever x is within delta (δ) values of p. In simple terms, f(x) approaches a limit L as x moves nearer to p. A complete delta-epsilon definition of will is discussed later in this section (Stewart, 2008). Mathematically, a limit is expressed as lim or by the right arrow (→) (Stewart, 2008). The limit of x at point n is thus expressed as lim(x_n) = x or x_n → x.

Limits as a mathematical concept are as old as math itself. Bolzano was the first mathematician to come up with modern definitions of the limit of a function in his epsilon-delta technique developed in 1817. Unfortunately, his work made very little contribution to the study of limits. Later on, Weierstrass developed a more elaborate epsilon-delta definition of a limit as expressed in the mathematical formula:

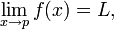
Mathematically, this can be stated to mean that the limit of f(x) as x approaches p is L if and only if, given ε > 0, there exists δ > 0 such that 0< |x- p| < δ implies that |f(x)-L| < ε (Pierce, 2009). In this definition, ε represents the given distance on either side of the limiting value y=L on the y-axis and δ is the distance on each side of the point x=p on the x-axis.

The formal epsilon-delta definition of a limit can be illustrated as follows. Michael is walking over a landscape represented by the graph y = f(x). The value x is used to measure his horizontal position and the coordinate y represents his altitude. His highest altitude as he approaches position p represents the limit L. His horizontal movement towards a position p is expressed as x = p when his altitude approaches L. This is a similar case as he moves past the position p. His altitude remains within L, but only up to a certain distance from p. Therefore, he can state his altitude at x = p as L even if his actual altitude is slightly lower than the L position. This means that his altitude gets nearer to L as he approaches or moves away from p, but with some accuracy goal that has to be met (Burton, 1997). That is, he has to be within a certain distance from either side of p to remain within L value. The accuracy goal represents the epsilon-delta definition of a limit stating that Michael’s altitude can be stated as L only if his altitude is within a certain distance from L whenever his horizontal distance is within a certain distance from p. From the formal definition of a limit stated above, the limit of a function f(x) made by Michael as he moves towards p is L if and only if for every distance between x and p the values of f(x) are within the limit L given an accuracy goal. For instance, if Michael movement from x to p is represented by a function f(x) = 2x+4 and his maximum altitude is 10m at 3m along with the horizontal distance p, then the limit of Michael’s movement towards a position p is expressed as lim 2x+ 4=10, x→3, if an only if for all ε >0, there exists a δ> 0 such that if 0< |x-3| < δ, then |2x +4 -10| < ε. Since we can fix values for Michael’s horizontal distance, but not his height, I will compute δ by manipulating this equation as follows |2x +4 -10| < ε so that the value inside the absolute value sign becomes x- 3 for both the δ and ε sides. When simplified |2x +4 -10| becomes |2x -6| = 2|x- 3| < ε. Simplifying it further, the final expression becomes |x-3| = ε/2. Since |x-3| represents the δ side of the expression, it can as well be written as δ = ε/2. Suppose we have a small ε = 0.6m then δ= 0.6/2 = 0.3m such that if 0< |x-3| < 0.3 then |2x+ 4-10| < 0.6. This, therefore, means that if an accuracy level is set at 0.6m from L, then Michael has to be within 0.3m on both sides of p in order to remain within the 10m altitude limit. However, as x approaches p, the delta- epsilon rule holds only up to a certain value above which δ = ε/2 would yield a value higher than 3. A bigger value of ε also makes the value f(x) arbitrary far from the L value. A summary of all ε values starting from 0.6 is provided in the table below.

Discuss l’Hopital’s rule

Limits are often in the form of algebra. Mathematically, the algebraic expression of limit is referred to as indeterminate. Algebraic expression of limits involves a replacement of sub-expression of a function by its limit. The resultant expression should provide enough information to aid in determining the original limit. If it does not, then it is referred to as an indeterminate form of expression (Burton, 1997). For instance, in the expressions lim x – 2/x ² – 4 and lim 1 – 3x²/4x² – 5x, the resultant function would be 0/0 at x=2 for the first expression and ∞/∞ for the second expression at x=∞. Both forms of expression are indeterminate forms as the resultant expressions provide no information to aid in determining the original limit expressions.

Indeterminate form of expressions is common in calculus. Either way, the limits of indeterminate forms of expression have to be determined. This is where l’Hôpital’s rule becomes applicable. l’Hôpital’s rule makes the evaluation of indeterminate expressions possible by using derivatives of the expressions. Thus the application of l’Hôpital’s rule converts an indeterminate form of the equation to a determinate form using the illustration outlined below:

If

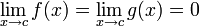
or ±∞ and

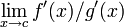
exists, then

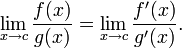
(adopted from O’Connor & Robertson, 2008)

This operation differentiates the numerator and denominator of the expression hence converting it from indeterminate to determinate form and thus making it easy to evaluate the limit of the expression (O’Connor, Robertson, 2008).

While l’Hôpital’s rule provides a perfect solution for evaluating limits of indeterminate forms of expressions in calculus, the rule does not apply in all cases. There are various instances whereby it is not appropriate to apply l’Hopital’s rule. That is, when the limits of the two parts of an equation are not 0, or are both infinite (O’Connor & Robertson, 2008). The following are indeterminate forms that are common in calculus: 0/0, ∞/∞, 0.∞, 1^∞, 0⁰, and ∞-∞. From these forms, L’Hopital’s rule is only applicable to 0/0, ∞/∞, and 0.∞, but the 0. ∞ the form has to be rewritten to 0/0 or ∞/∞ form first (Stewart, 2008). In other words, l’Hopital’s rule only applies to quotients and not products. For Example: lim_x->0 + (cos x)/x

This implies positive infinity because the numerator approaches 1 while the denominator approaches 0. If l’Hopital’s rule is applied, we get lim_x->0⁺ (- sin x)/1 = 0, which is incorrect. We can avoid applying L’Hopital’s rule if it makes the problem worse or if there is an easier way to get the answer. In this regard, it is important to first prove the applicability of l’Hôpital’s rule before applying it. In calculus, this is done using Cauchy’s mean value theorem.

Discuss the concept of the derivative of a function

In calculus, the derivative is a measure of the changing relationship between a function and its input (Spivak, 1994). That is, how much one quantity is changing in response to changes in some other quantities. For example, an object moves at a speed that can be computed using the time it takes to complete a given distance. Its instantaneous velocity thus represents the derivative of the function of distance and time. Therefore, the derivative of a function of the moving object at a stated distance p represents the best ever a linear approximation of the function of the object over the distance p (Spivak, 1994). Therefore, the derivative of f(x) at each point along p represents the slope of the graph x makes with every input of p. In other words, the derivative of x at point p is a linear transformation of f(x) commonly referred to as linearization of f(x) at p. Derivatives are computed through the process of differentiation.

Differentiation operations are common in single-variable calculus. In calculus, a function is said to be differentiable at a point where it is also continuous (Spivak, 1994). For example, let the step function f that returns p to its original point when all x values are equal to or less than p be 1 and 10 when x values are greater than or equal to p. In this example it is impossible for f to be differentiable at p since if x is negative, then p+ x would yield a value lower than the slope line and the slope would be approaching infinity as x approaches 0. Similarly a positive of h will yield a zero. Hence, the limit of the different quotient is nonexistent as the secant forms no slope in both directions.

The relationship between continuity and differentiability where y=x can be illustrated as follows.

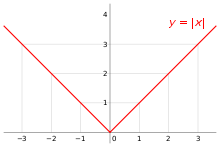
This graph portrays the perfect illustration of continuity and differentiability. For instance, at point x = 1, the absolute value function is continuous and differentiable whereas it is only continuous at point x = 0. At point x = 0, the graph of the absolute value function f(x) = |x| has a sharp corner. This is attributed to the fact that the tangent slope approach different value from the left, i.e., y = -|x|, while it is y = |x| from the right hence not continuous at point x = 0. However, a function may still fail to be differentiated even if it is continuous at that point. For instance, in the above graph, the value of x directly influences the slope of the secant line from 0 in that a positive value of x yields a positive value of the slope and vis-a-vis for a negative value hence the impossibility of differentiability of the absolute value of y = |x| despite its continuity at the same point (Spivak, 1994). This appears as a “cusp” in the graph at the point x = 0. Generally, most functions with smooth graphs are not differentiable at point x = 0 with exception of a few (Spivak, 1994). That is, the function y = ³√x is not differentiable at x = 0. Therefore, for a function ƒ to have a derivative it is essential that the function ƒ be continuous.

Differentiation and integration are interrelated concepts in calculus. Their relationship is generalized using the concepts of integration and absolute continuity. Continuity implies integrability even over closed intervals, i.e., if a function f is continuous on the closed interval [a, b], then f is integrable on [a, b] (Fundamental theorem of calculus). For functions with real value measurements, there is absolute continuity of functions and absolute integrability of measures along a line (Bartle, 1995). Hence, continuity of a function implies integrability, but integrability does not imply continuity. Some functions are integrable over intervals where they are discontinuous. To illustrate this point, let us consider the example below over the interval [0, 2].

• f(x)= 1 for x ≠ 1 in the upper partition and
• f(x) = 0 for x = 1 in the lower partition

Considering P to be any partition in the interval [0, 2], the upper sum U(f, P) will be 2 while the lower sum L(f, P) will be less than two since any subinterval with a value x=1 contributes zero on the lower partition hence constituting a discontinuity. This function is however integrable. To prove this, I will rely on the theorem of Reimann integrable, which states that: if f : [a, b] → R is bounded, and f is integrable on [c, b] for all c ε (a, b), then f is integrable on [a, b] (Fundamental theorem of calculus). In this case, I will consider c to be a subinterval x=1 along [0, 2]. Let ε > 0, considering the partition P_ε = . The lower sum L (f, P _ε) = 1(1- ε/3) + 0(ε) + 1(1- ε/3) = 2 – 2/3ε Remember the upper partition U(f, P _ε) was 2. For a bounded function to be integrable over an interval, the difference between the upper and the lower sums should be arbitrarily small. Therefore, 2- (2-2/3 ε) = 2/3 ε < ε, hence this function is integrable over [1, 2] and subsequently [0,2] based on the provision of the theorem stated above.

References

Bartle R.G. (1995). The Elements of Integration and Lebesgue Measure. Wiley Classics Library. New York: John Wiley and Sons Inc.

Burton, D. M. (1997). The history of mathematics: An introduction (3^rd Ed.). New York: McGraw Hill.

O’Connor, J. J., & Robertson, E.F. (2011). De l’Hopital biography. The Mactutor History of Mathematics Archive. Scotland: School of Mathematics and Statistics, University of St. Andrews.

Pierce, Rod. (2009). “Limits (Formal Definition)”. Math Is Fun.

Spivak, M. (1994). Calculus. Houston, Texas: Publish or Perish.

Stewart, J. (2008). Calculus: Early transcendental (6^th Ed.) Thomson: Brooks/Cole.