Introduction
In a world of data, measuring the complexity of its interpretation and the amount of information that is encoded in the data is a research priority. If one imagines that a particular bit of information is encoded in a single string, then the complexity of describing this string is determined by the availability of a way to compress this string to a minimum size so that the compression fully describes the complexity of the initial string. Obviously, however, not all strings can be compressed to a minimum number of characters. In this regard, it was decided to introduce the notion of Kolmogorov complexity describing the maximum degree of compression by the best existing compressor in some universal description language as a theoretical model. However, there is sufficient evidence that Kolmogorov complexity is not computable. In this sense, one should mention the model of the cost of a positive integer as an attempt to represent Kolmogorov complexity in a more straightforward, more comprehensible language. In general, the cost of a positive integer describes the complexity of representing any positive integer in a data set as the sum or product of smaller numbers from the same set. This research paper examines and describes in detail the phenomenon of the cost of a positive integer and outlines the limits of its applicability.
Definition: Kolmogorov Complexity
Any information written with a computer program is defined by symbolic sequences. In turn, information encoded in symbols can be repeated several times, especially if a given string is created through copying. This is how systems work in which patterns are detected — for example, the following string
contains eighteen zeros. This entry itself, presented in [1], is a representation of itself, but there is a more straightforward way in which this string can be represented, which is:
In this case, one can see that instead of 18 characters, the same information is now encoded with eight, which allowed to compress of the original data array by about 55 percent. Actually, the program itself which allows to compress the original [1] to [2] is the Kolmogorov complexity of a string (Resch). However, not all strings can be compressed in a similar way. For example, the string [3]
contains some valuable information and cannot be represented in any other, shorter way than it itself since no pattern of symbol repetition is detectable. The algorithmic complexity of a string [3] is said to be random and without apparent regularities. However, there is no guarantee that actual but non-obvious regularities are not there since mathematics is much deeper than surface perception and information processing with the eyes. One could use quantum computers with machine learning techniques that could surely solve the problem of inferring a string’s shortest path [3] than “16731180221965342229”, but this is not really possible. The impossibility of programs for uncountable strings with random Kolmogorov complexity is postulated by a fundamental theorem of the mathematical section of information. In reality, no mechanical machine will be able to pick the optimal way to display such data, and even if a pattern is found, this does not guarantee the existence of a “more” optimal version. This postulate is associated with the halting problem of Alan Turing, who proved that mechanical machines could not accurately determine whether a program can terminate or will run without stopping (Lucas 9). Thus, both Kolmogorov complexity and Turing’s halting problem are incalculable problems in the theory of computing algorithms.
The Cost of a Positive Integer
Understanding the principle of Kolmogorov complexity is critical to studying the phenomenon of the cost of a positive integer. The term was first used by Dr. William Calhoun, who, in 2005, at the Cheap Integers math contest, decided to create some analogy of Kolmogorov complexity, but a more straightforward and computable one (Norfolk 1). The potential of such an idea is high: with the help of Calhoun’s function, it would become possible to compress any array to its minimum content while maintaining the integrity of the data. This would be a real solution to the problem of big data and limited memory in electronic devices and would speed up data exchange between clients. In creating the cost function of a positive integer, C(m), Calhoun used the following considerations:
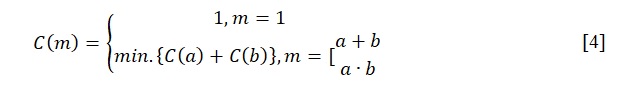
Or, in one line for m≠1:
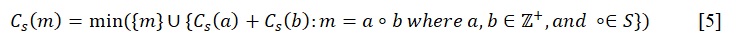
Based on [5], it is easy to conclude that the value of a positive integer is determined by at least two operations, whether summation or multiplication. Consequently, since one of the two operations for a finite number of smaller numbers must be applied to identify the conditional third term of the data set, the Calhoun function is recursive (AVU). In addition, this definition uses many binary operations, which are noted as follows:
From fundamental mathematics, this expression can mean any of the six kinds of classical operations on binary operations, but Calhoun’s model uses either multiplication or summation. Based on the above, one can formulate an extremely important lemma. Thus, for any set of binary operations S and for any positive integer m, there exists a Calhoun function such that:
In other words, the computed value of a positive integer will always be numerically equal to or smaller than the positive integer itself, and this is an extremely important consequence of the Calhoun model. However, for [5], there is only one function, Cs, that uniquely describes the set S and satisfies the definition of the value of a positive integer. Another critical consequence follows from the above: if the number of operations in S is finite, then Cs is an evaluable function, unlike the Kolmogorov complexity of a string.
Some Additional Consequences
In fact, the positive integer cost function described in the previous section is a multi-valued mathematical model from which several valuable conclusions can be drawn. Recall that Cs is defined as a minimum of possible binary operations on smaller positive integers. Thus, if a prime number Y was taken as an initial number, then
This statement is easily verified by any example with a prime number, such as a three:
This is not surprising since three cannot be represented as the product of two smaller numbers satisfying Z+, and hence the number three itself is the minimal possible representation of itself. Moreover, if:
Then,
In [10] and [11], x and y represent the minimal possible numbers with which any non-prime number can be represented. For example, for the digit 6, and are, respectively, two and three, hence:
Notably, x and y do not necessarily have to be different digits: the only restriction imposed on them — besides belonging to Z+, — is that the binary operation performed on them must be minimal, according to the Calhoun model. Thus, for m=4, x and y both equal 2:
It is easy to see that these conclusions are valid for C, that is if multiplication was used as a binary operation. If, however, the variability of such operations increases — which means that in addition to multiplication, one can now use addition as well — then new consequences are added. For example, a positive integer m can be called multiplicative if:
Not all numbers have this property, so it was necessary to create a term to describe some of the datasets that satisfy the entire multiplicity property. In addition, one can notice that:
Based on all of the above, it is appropriate to illustrate all properties, lemmas, and definitions with a general example. Hence, by now, it is precisely known that the Calhoun model uses either multiplication or addition as variations of binary operations, with the cost function of a positive integer applying either of these operations whose result will be numerically smaller. Thus, the following table can be created for the set of the first ten digits of Z+:
Table 1. An example of positive integer cost functions for numbers from 1 to 10.
Several essential aspects should be discussed in Table 1 to reinforce information about the Calhoun function. First, it is in the researcher’s power to impose restrictions on the use of a particular binary operation: it can be multiplication or addition. Second, for this procedure, numbers are decomposed into a and b, that is, the factors of a given number if it is not prime. Third, these factors are either summed or multiplied: the smallest of these values is used as the value of the function. Table 1 also confirms the corollary [14]. Fully multiplicative numbers are each of the set of given numbers except 7. In the case of m=7, the product of factors is less than their sum:
It is noteworthy that fully multiplicative numbers can be represented in the following form:
For example, Table 1 shows that the number 9 is fully multiplicative, so it can be represented as:
where a and c are both equal to zero. Here are some more examples of how various multiplicative numbers can be represented:
Table 2. Examples of decomposition of fully multiplicative numbers 2, 6, and 10.
From Table 1 one can make one more important observation. It turns out that for any m≥6 the following is true:
This is perfectly verified for m satisfying the condition m≥6.
Setting Boundaries
Calhoun’s function interestingly describes the properties of any number — in fact, any information — to be represented as a smaller number of signs. However, the essential question is how big or small the information compression values can be according to this function. To this end, Norfolk (6) describes two functions by which lower and upper bounds can be calculated for each particular number m, respectively:

where a is some number from the set Z. Thus, if m was equal to 4, then the lower and upper limits of contraction will be equal to:
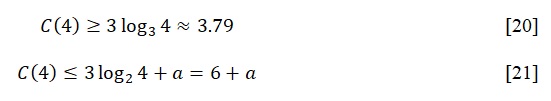
Conclusion
In conclusion, it is worth emphasizing that mathematics is dynamic, and having theorems and axioms can be disproved or viewed from a slightly different perspective over time. Kolmogorov complexity is one such phenomenon: in the general case, this model shows the impossibility of computing a program that could define a minimally compressed model that fully encodes some information. In 2005, William Calhoun partially circumvented this prohibition by forming a value function of a positive integer. This function describes the ability of a number m to be compressed to Cs(m) values, in which each number is described by either the sum or the product of its component, depending on the value of their result. The potential of such a model is great: it allows us to calculate the Kolmogorov complexity and compress any data set conditionally. This includes big data, as shown in mnorfolk03, which calculated the value of positive integers up to 1000 (Mnorfolk03, 2021). This is a vast array of finite data, which means that increasing it to m = 10,000 or even 1,000,000 will prove to be an even more complex product.
Works Cited
AVU. “Activity 1 – Recursive Algorithm.”LibreTexts, 2021, Web.
Lucas, Salvador. “The Origins of the Halting Problem.” Journal of Logical and Algebraic Methods in Programming, vol. 121, 2021, pp. 1-9.
Mnorfolk03. “table.md.”GitHub, 2020, Web.
Norfolk, Maxwell. “The Cost of a Positive integer.” Rose-Hulman Undergraduate Mathematics Journal, vol. 22, no. 1, 2021, pp. 1-12.
Resch, Nicolas. “CS 252, Lecture 4: Kolmogorov Complexity.”CMU, 2020, Web.