Introduction
Laboratory work investigated the dependence of the vertical displacement of a holding device (band, spring) depending on the applied force. An elastic band, a short spring, and a long spring were used in experiments to observe their stretching when weights of different masses were suspended from them. Through the masses, the corresponding values of gravity were obtained.
Analysis
To obtain the data, nine tests were performed, three for each type of restraint, as shown in Table 1. The second column corresponds to the spring’s initial position before the weight was attached, so this value is constant within each of the rounds. The third column is the new value of the spring or belt position when the weight shown in the last column of the table is attached to it. The difference between the initial and final values of the position of the lower end of the spring corresponds to the vertical displacement, that is, it shows how much the given weight was able to stretch the holding device.
Table 1: Empirical data from nine trials.
Three restraints were used: an elastic band, a long spring, and a short spring. As can be seen, unique values were true for each of the stretches, which was entirely due to both the type of restraining device and the mass of the suspended weight. Since gravity (F = mg) acts on the suspended weight, it was possible to determine force values for each test (Smart Apple Education Academy, 2020). The acceleration of free fall was assumed to be 9.81 m/s2, and it was considered that the weights were measured in grams. Table 2 shows the results of the force calculations for each of the tests.
Table 2: Results of calculations of the values of gravity forces affecting the weights.
Since the gravity forces were determined based only on the mass of the weight and a constant value of the free-fall acceleration, the results were identical. At the same time, the applied gravity forces stretched the holding device differently due to the mechanical features of the springs and belts. In order to study this pattern, the dependencies of the displacement on the applied gravity force were plotted. However, it should be kept in mind that each of the restraints had unique tensile coefficient values, so it was not acceptable to depict a single relationship for all of them. For this reason, three linear dependencies were visualized: one for each device. Figure 1 shows these dependencies with the corresponding coefficients of determination.
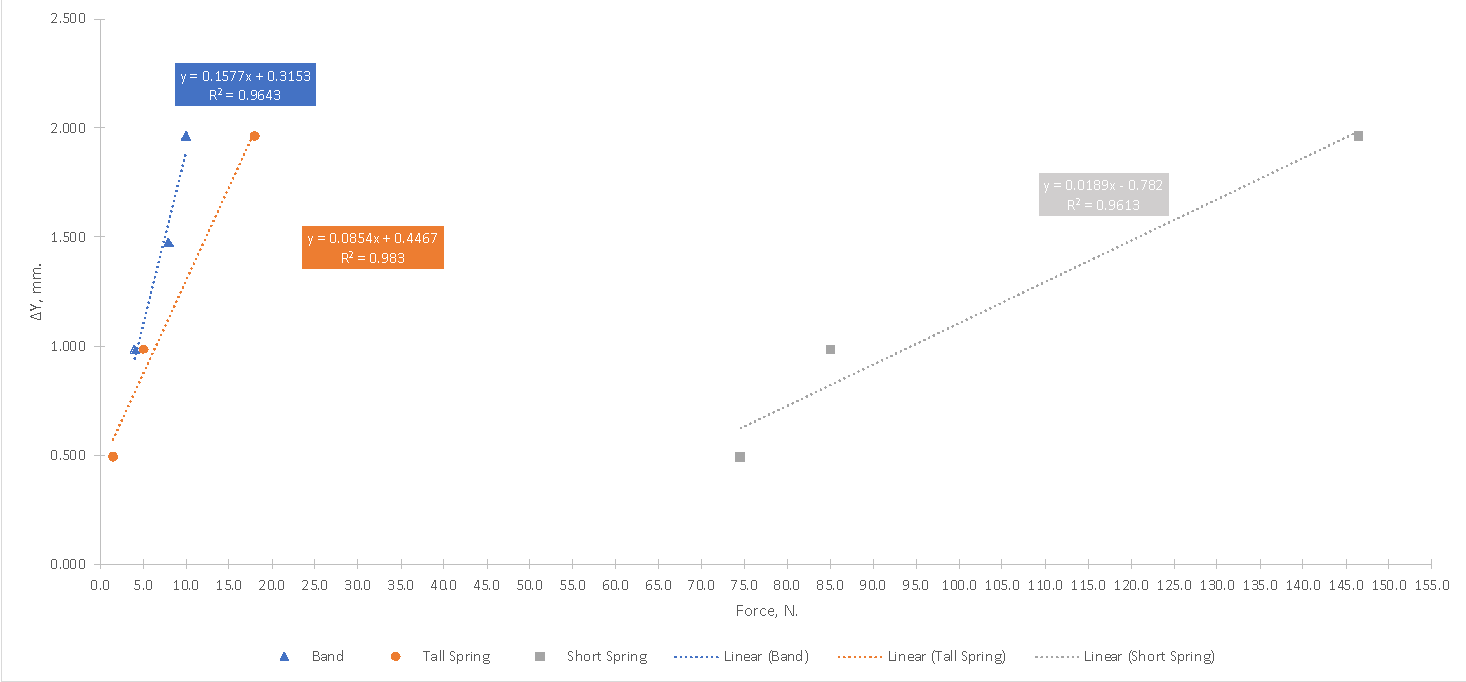
From the R2 values, it is clearly seen that linear approximations are well satisfied by these sets, so no additional linearization was required. This means that as the force applied to the weight increases (that is, as the weight mass increases), the vertical displacement tends to increase linearly, which seems quite logical. It is noteworthy that the slope values were quite different: the strongest slope was true for the elastic band, while the slowest growth was observed for the short spring. The y-intercept value is the definition of the displacement value at the moment of zero force and makes no physical sense because when there was no force, no displacement should have been observed. The inverse value of the slope (s2/kg) also makes physical sense and determines the stiffness of the restraining device, be it spring or a band. Thus, the stiffness of the elastic band was determined to be the minimum, and for the short spring, the stiffness was the maximum.
Conclusion
It has been shown that the vertical displacement of the linear is related to the applied force of gravity, which means that there is an increase in displacement as the force of gravity increases. Visually, this is observed as an increase in the extension of the restraint as the mass of the suspended weights increases. The physical meaning of the inverse of the slope as the stiffness coefficient of the corresponding device was also shown: for a short spring, the stiffness was determined to be maximum.
Reference
Smart Apple Education Academy. (2020). Fg = mg practice problem | finding the gravitational force on an object | educational physics video. YouTube.