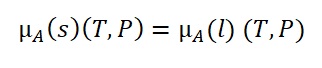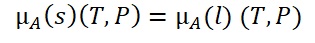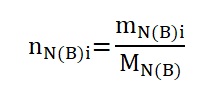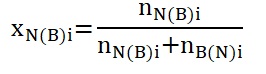Introduction
The cooling curves of the pure compounds and various mixtures were used to construct a solid-liquid phase diagram of the biphenyl and naphthalene systems. A phase diagram shows melting, freezing, vaporization, and sublimation. These graphs represent the temperature, pressure, and composition relationships. One of the easiest ways is to use cooling curves to create phase diagrams and determine phase transition temperatures.
The melting point of a substance may be determined by measuring the rate at which it cools from a liquid to a solid at a constant atmospheric pressure. Assuming the composition of the samples is known, the rate at which each combination cools may be used to establish the eutectic temperature. Eutectic systems are those in which the melting or solidifying point is lower than the melting point of any one component. The binary phase diagram illustrates the combined cooling curves of the two components to show how each affects the total cooling of the solution.
Each component of the mixture contributes to the solution’s solidification as it cools. At a given time, one of the components will begin to solidify, which may be referred to as compound Y. This slows the cooling process, as seen by the graph’s decreasing slope. Since compound Y is in the solid state, the liquid becomes enriched in compound X, which rises until the eutectic point. A eutectic point will be reached at this moment when both chemicals X and Y have solidified, and the temperature will no longer change.
The cooling of the mixture will continue after the solidification of the mixture has occurred at a pace defined by the heat capacities of the two solids and the composition of the provided mixture. The binary system’s phase diagram may then be mapped using the pure and depressed melting points. From this, the limiting tangent slopes may be used to determine the enthalpy of fusion for each component.
The chemical potential of solid X in a mixture is stated to be the same as pure solid Y at the same temperature and pressure. The following equation (1) can be used to describe the liquid and solid phases of a component’s potential chemical relationship at pressure P and temperature T.
The chemical potential relationship of pure solid A and solid A in the mixture can thus be determined using equation (2)
Using Raoult’s law, one may determine the chemical potential of a liquid at equilibrium based on its activity. In this experiment, naphthalene and biphenyl mixtures are observed. N-N and B-B interactions (N representing naphthalene and B representing biphenyl) in the liquid phase are assumed analogous to the N-B interactions in the solid phase.
where n – number of moles, m – a mass of the chemical compound, M – molar mass.
where XN(B)i – a molar fraction of naphthalene (N) or biphenyl (B) in the composition
Reagents
- Pure Biphenyl
- Pure Naphthalene
Procedure
Preparation of the sample
- Weigh 2g of naphthalene on filter paper, then transfer it into a small test tube with caution.
- Insert a rubber stopper in the sample tube, then put the sample into a beaker filled with boiling water.
- Once the sample has dissolved, remove it, and place it in ice water to let it cool.
- Insert the probe by removing the stopper while ensuring the PTFE spacer keeps the probe centered.
- The tip of the probe should be in the lower third of the melted sample, so not all the way down where it would touch the stirring bar because if it does it would affect the graphing of the sample.
- Record the temperature readings up to 10oC to obtain the cooling curve.
- Place the sample tube in boiling water until it melts, and then remove the probe.
- Let the molten sample cool and add 0.2g of biphenyl.
- Melt the mixture and swirl to homogenize the liquid.
- Once the sample has dissolved, remove it, and place it in ice water to let it cool.
- Remove the sample from the ice water bathe, heat the solid, remove the probe, and add another 0.4g, 1g, and 2g of biphenyl to the sample mixture simultaneously to obtain the cooling curve for each.
- Follow the same procedure but start with 2g of biphenyl to obtain the cooling curve.
- Add 0.2g naphthalene to this sample to obtain the cooling curve.
- Repeat the above step for 0.4g and another 0.4g of naphthalene to the biphenyl sample to obtain the cooling curve for each. The total for the cooling curves would be 9 at the end.
Computer-Assisted Data
- Initiate the data acquisition software to record the data for the cooling curve of each sample.
- Save the data file and record the file name.
Results
First, the cooling curves for all the nine mixtures were determined, and the results can be found in Figures 1 and 2 for 2 grams of naphthalene + 0.2/0.4(1)/0.4(2)/1 grams of biphenyl and 2 grams of biphenyl + 0.2/0.4(1)/0.4(2) grams of naphthalene accordingly. Based on these graphs, the final solidification temperatures (freezing points) were identified and documented in Table 1.
Table 1. Determining Freezing Points for Various Mixtures.
Next, to determine the mole fraction for both biphenyl and naphthalene solutions, it is necessary first to calculate the number of moles of each component in different samples using equation #3. Therefore, the sample estimation for the first sample (pure naphthalene) is as follows:

The results for other samples can be seen in Table 2. Note that the molar mass for naphthalene and biphenyl was estimated using formula #4. Thus, as the former reagent consists of 10 carbons and 8 hydrogens, the molar mass equals 128.1705. On the other hand, the latter reagent consists of 12 carbons and 10 hydrogens, and therefore, its molecular weight is 154.2078. Now, it is possible to determine the mole fraction of naphthalene and biphenyl using equation #5. The mole fraction of the former organic compound for sample #2 is calculated as:
Similarly, the mole fractions of both components were calculated, and the results can be found in Table 2.
Table 2. Sample Molar Composition and Mole Fraction.
Based on the received mole fraction rate and temperature values, it is possible to construct a phase diagram and identify the measured eutectic point in which solid and liquid phases are in thermodynamic equilibrium. The latter indicates the lowest melting point among all the studied mixtures and equals 312.26 against xN = 0.42 which can be observed in Figure 1.
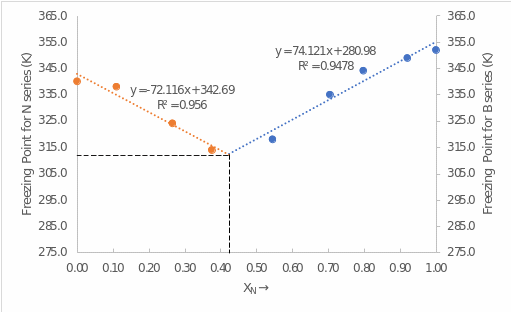
Corresponding regression equations for the two substances:
Naphthalene:
Biphenyl:
Hence,
The next step was plotting the mole fraction of naphthalene and biphenyl against the depressed freezing point. Figure 2 shows the corresponding dependence plot for the mole fraction of naphthalene and Figure 3 for biphenyl. It is noteworthy that in both cases only three points are used: the pure substance and the first two additions of the corresponding reagent.
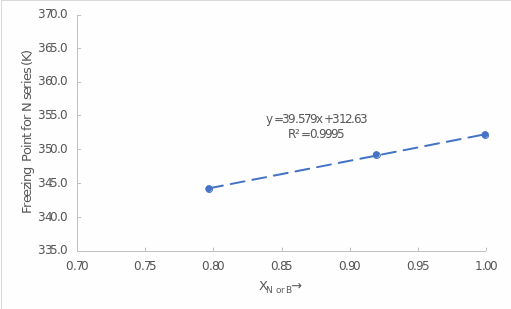
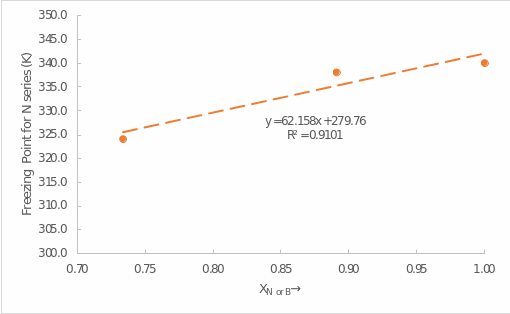
As can be seen, a linear regression was used for both data sets, and it is interesting that the linear trend was more significant for the mole fraction of naphthalene. It follows that as naphthalene or biphenyl was mixed with the appropriate reagent, there was a consistent decrease in the freezing point. In addition, the use of linear regression equation coefficients for each of the plots allows us to estimate the value of
. For naphthalene, the following calculations are correct:
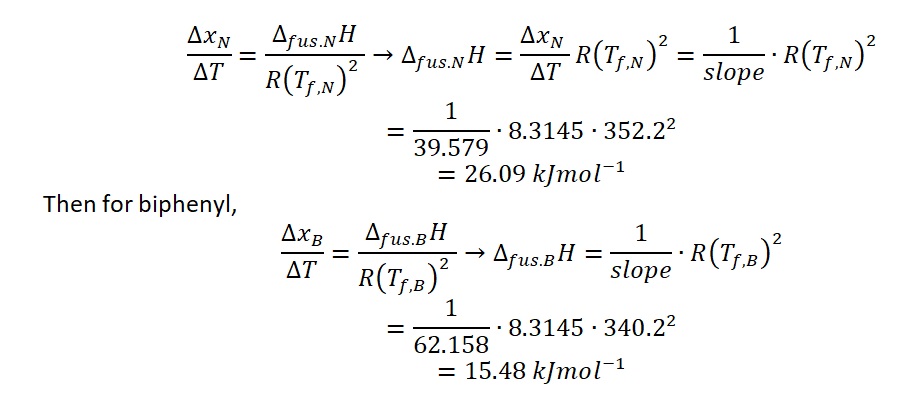
Thus, the values of
were determined for the two substances. It can be seen that for pure naphthalene this value is higher by about 1.7 times than for biphenyl.
Discussion
This experiment determined how the melting point of the naphthalene-biphenyl system changed according to the composition of the solution. As expected, the freezing point of pure naphthalene and biphenyl gradually reduced when mixed with the second compound. For instance, the melting point of pure naphthalene was 352.2 K, but when the 0.6 grams of biphenyl were added, the final solidification temperature was equal to 344.2 K. Yet, such temperature reduction persisted only until a certain threshold – eutectic point – was reached, which is the lowest melting point for the naphthalene-biphenyl binary system.
The thermodynamic equilibrium point between the solid and liquid phases was determined by plotting the graphs of both functions on a single coordinate system and determining their intersection point. Thus, it was found that eutectic temperature is equal to 312.26 K while eutectic composition includes 0.42 of naphthalene and 0.58 of biphenyl.
Next, it is necessary to compare the values received during this experiment with those generally accepted in the literature. According to previous research conducted by the National Institute of Standard and Technology (2021a, 2021b), the melting points of pure biphenyl and naphthalene are 342.15 K and 353.15 K.
Additionally, Hua et al. (2010) determined that the eutectic temperature is 314.15 K while the composition of naphthalene to biphenyl is 40% against 60%, respectively. Contrary, in the current study, the ideal solubility curves with a eutectic temperature equal to 312.26 K and 42% of naphthalene percent in the composition. Therefore, it can be concluded that the findings of this study are very close to those of previous research, but differ from the ideal eutectic point, although not greatly.
Finally, the heat of fusion was calculated for both compounds, where the
, and
. Nevertheless, these results were different from the ones obtained by previous studies. In this regard, previous findings suggest that
has varying values from
to
, average, 17.85. (National Institute of Standard and Technology, 2021b). On the other hand,
equals the number in the range from
to
, average, 19.14 (National Institute of Standard and Technology, 2021a). Therefore, it can be concluded that there is a significant difference between the results obtained during this study and the ones found in the previous literature.
Conclusion
In summary, the current research presented the cooling curves of two pure chemical components, namely biphenyl and naphthalene, and their mixtures. Moreover, it intended to identify the melting points of each studied sample and based on this information, determine the eutectic composition and temperature. It was found that the melting points for pure naphthalene and biphenyl are equal to 352.2 K and 340.2 K, respectively, which is almost in line with the generally accepted values.
As for the eutectic point, both the eutectic temperature and composition were close to the numbers received in a previous study. Yet, as for the values received by plotting the ideal solubility curves, both the eutectic composition and temperature were significantly different but still relatively close to the values claimed by this study and previous research.
References
Hua, D., Hong, J., Hu, X., Hong, Y., & Li, J. (2010). Solid–liquid–gas equilibrium of the naphthalene–biphenyl–CO2 system: Measurement and modeling. Fluid Phase Equilibria, 299(1), 109-115.
National Institute of Standard and Technology. (2021a). Biphenyl. Web.
(n.d.). Solid-Liquid Equilibrium in a Binary System. Unknown