Introduction
It would be partially biased to imply that people are exclusively motivated by their material self-interest (Roth, 1993) when placed in a situation whereby they have to decide on the number of good things that they can keep for themselves and that amount that they can comfortably share out with others; an economic decision (Lebow, 1996). This is depicted in the Ultimatum game whereby a pair of subjects has been placed in a decision whereby they have to agree on the division of a fixed sum of money.
People are divided into two groups; group one is that of people who have scored highly on a visual exam with the other group comprising of those who have not scored as highly. Several factors may influence the decision that a person makes during a case whereby they are supposed to share resources like money with others, and not mere self-interest.
Methodology
The first game begins with the division of a group of people into two groups based on a criterion that analyzes how they answer questions in a given evaluation session. The first group consists of the top fifteen performers within the group with the bottom fifteen being placed into the second group. The group with the top performers is sent to a room and given the title of proposers while the second group is sent to yet another different room and given the title of responders. The rooms are set in such a way that there is no contact between the proposers and responders, the members of one room not knowing the identity of the members in the other room.
The proposers are then given some defined amount of money then asked to share this out with another member of the group of responders. These proposers are freely allowed to propose how they want to divide their money with another person in the other group; a person that they know nothing about and have probably never met (Cruger, 2002). This person referred to as the responder is allowed to view this proposal but does not know specifically from whom it came. After viewing and analyzing the proposal, they are allowed to either accept or reject this proposal, the latter of which leads to a situation where neither of them receives the money.
The first game was played in two rounds within the experiment whereby one proposer is allowed to make several proposals to different responders in the other room. This communication is carried out through the use of a messenger who delivers the message of the offer from the proposer to the responder and then collects all the cards as part of feedback for the game. These rounds are carried out under different scenarios including a limit session whereby the amount that the proposer can offer the respondent is limited to a certain minimum amount. This allows for the respondent to receive values above a certain level that can be as low a $0 and as high as half the amount initially given to the proposer.
The second game on the other hand is played through the use of a website and requires the use of a computer terminal. At the beginning of the game, each user is provided with a specified user name and password that they are to use to identify themselves with the system. It is these that they use to log into the system and begin playing the game. After logging in, they are allowed to participate in a visual perception contest in which the top performers are assigned to a group known as the proposers, and the remaining half are assigned to the group of responders.
Once assigned the role of proposers, a member receives $55 which they are asked to share with the members of the other group; the responders. If the responder accepts the proposal then the proposer is given $55 less the amount offered to the responder while the responder gets the actual amount offered by the proposer. If the responder rejects the offer then none of the players get anything. Each responder and the proposer will make contact only once during the game and may not repeat themselves with a total of ten rounds having been played during that second game. Payment will be done based on only one of the offers that are made by the proposers and will be chosen randomly. Anonymity will be ensured in this game through the use of no messengers between the proposers and responders. Payment will also be done by another experimenter who does cannot identify the players who have participated in the experiment.
In light of this, there may be very few responders who reject the particular proposals that they have been offered because both the proposers and the responders are only interested in the amount of money that they can receive from the game. The proposer knows that the responder is rational and selfish and will not reject his money no matter how little it is. In such a case, the proposer acts by offering only a small amount of money to the responder while keeping as much as possible to himself; knowing all too well that the responder will not reject his proposal. This concept purports the theory of self-interest with the hypothesis that people are exclusively motivated by their self-interest as seen in cooperative institutions and voting behavior manifested by people all over the world (Samuelson, 1998).
Results
Two sessions were conducted during the first game and were classified as the base session and the limit session. The results that were obtained in each of these sessions are tabled below:
The base session was the initial session that was conducted whereby the proposers were initially told to offer a certain amount of the free money that they had been given to the other person. The limit session was enforced by stating a minimum amount of money that could be offered to the responder. This is to say that that proposer was given a minimum amount of money that he could offer to the responder and nothing less. During these sessions, the responder’s actions were documented and it was noted as to whether they accepted or rejected the offer.
During the base session, two rounds were conducted and during the first round, it was noted that 50 percent of the groups offered a uniform amount of money to the respondents that they interacted with during the complete round. The other half interchanged the amount of money that they offered with a range of about $5 with the lowest offer made to a particular responder being $5 and the highest amount being $30. During the second session, 66.6 percent of the proposers offered the same amount of money to different anonymous responders. The remaining offered varying amounts of money to the responders within the range of $5 with the lowest and highest amounts being offered to be similar to those of the first round. Out of the 72 offers that were made during the second round, 12.5 percent were rejected. Payments during the game were made during the second round with 19.04 percent out of the initial 87.5 who accepted the proposals being paid.
The chart below illustrates the total number of base proposals that were accepted and those that were rejected.
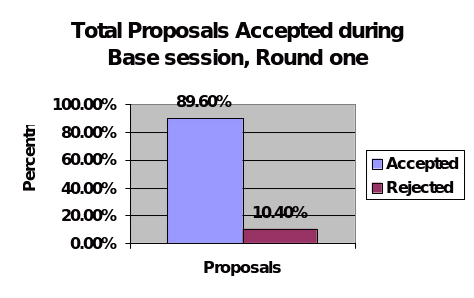
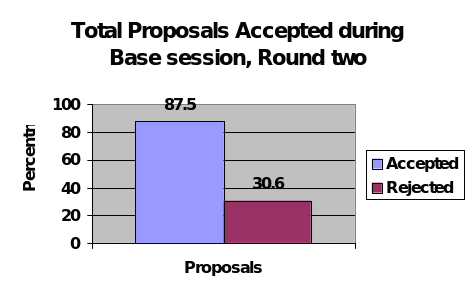
During the limited session, there were also two rounds that were conducted with each round having its own payment schedule. 33.3 percent of the proposers offered a similar amount of money to anonymous responders throughout the first round. The remaining 66.7 percent offered varying amounts of money to the responders with the highest amount being $30 and the lowest amount being $5. Odd figures like $8 and $28 were also offered by proposers during this stage to some of the anonymous responders.
Out of the 98 offers that were made by proposers throughout the first round of the limit session, 13.2 percent rejected the proposals made to them while 87.8 percent of them accepted. This can be illustrated in the chart below that shows the percentage of responders who either accepted or rejected the offers of money that were made to them by the proposers.
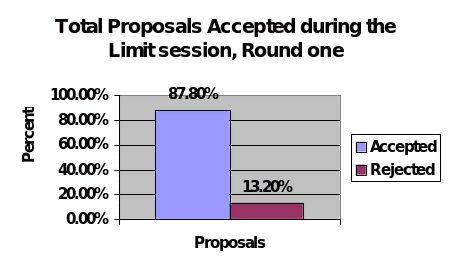
Out of the total proposals that were accepted, a total of 16.47 percent were paid the amounts that they had been promised had they accepted the proposals made to them during the session.
During the second round of the limit session, a similar 33.3 percent of the proposers offered a similar amount of money to anonymous responders throughout the first round. The remaining 66.7 percent offered varying amounts of money to the responders with the highest amount being $30 and the lowest amount being $5.
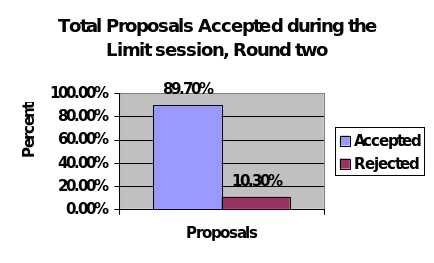
Out of the 98 offers that were made by proposers throughout the second round of the limit session, 10.3 percent rejected the proposals made to them while 89.7 percent of them accepted. There were no payments that were made to the players during the second round of this game.
Through the use of limits, the game cum experiment was used to gauge whether there could be significant differences in the amounts that the proposers offered to the responders between the two rounds that were conducted under different social environments.
There was indeed a significant difference in the levels of money that were offered in the two scenarios with each being able to be carefully explained by some of the models and theories that govern the choices that a person will make when faced with this type of situation.
During the second game, a total of 74.8 percent of the total proposals were accepted out of the ten rounds that were conducted; this was slightly lower than what was observed in the first game.
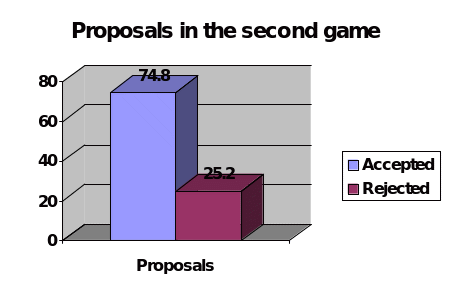
There were also several participants (87.2 percent) who offered a similar amount of money to the responders during the full rounds that the games played; very few of them alternated or changed the amount of money that they offered to the responders. It is also interestingly in this second game that the largest offer of $40 was made to one responder. A consideration of the first and second round in this second game resulted in data listed in the table below:
Through the use of Pearson’s coefficient, a careful statistical analysis of the information is carried out to determine the relationship between the type of session and the amount of money that is offered to the responders.
The results of this study yielded a p-value of 0.6788 which allows for a correlation between the type of session and the level of rejection among the groups. In the presence of an experimenter, it is observed that there is a higher level of rejection among the responders possibly due to the nature of offers that they are given. As a result of the significant difference between the variables that have been related above, the null hypothesis of no difference is rejected in favor of the alternative hypothesis that clearly depicts a difference in the values that are obtained during the different sessions. It can thus be inferred that self-interest is not a major motivator during the game and there are other factors that also significantly affect the outcome of the game.
Discussion
The Ultimatum game exhibits the feature of simplicity that allows the experimental subjects to completely understand the rules of the game and the implication of each of their actions before they undertake them (Roth, 1993). This type of game also makes it easy to identify the traits of a person because it allows for one to adopt specific dominant strategies that will allow him to earn more money thus making him self interested such that it is easy to identify any person not using these strategies (Cruger, 2002). In such a case, the strategy has been availed to the player but they deliberately choose to ignore them, choosing different moves that allow an observer to make inferences about his motives in the game. This is to say that most people will in this case only agree to give out the lowest possible amount of money to the responder in the hope that he may gain more money while keeping that which he already has. But then there are those people that give out a substantially higher amount of money to the responder with other interesting motives behind their strategies making the observer wonder what they are really up to.
The game involves a classic case of bargaining whereby communication between the bargainers is limited to making offers and accepting or rejecting them with a predetermined set of rules governing the decisions that they make in light of this (Schmidt, 2006). In a normal bargaining environment, both users are allowed a complete channel for communication whereby the proposer makes his offer which is then challenged by the responder who makes another type or proposal which the proposer can either accept or decline, prompting another proposal (Davis & Holt, 1993). This process goes on until a figure is reached whereby both parties are comfortable and none feels downplayed.
The outcome of the game, when compared to other similar games that were conducted in the same manner but with the proposer making eye contact with the responder, achieved a different result. It was observed that there was bargaining between the proposer and the responder whereby the responder was able to refuse and challenge the amount that the proposer issued (Bimore, 2002).
Face-to-face communication between the two also took a lot of time and effort as a result of the exchange of words, ideas, and arguments between the two parties. In this case, the proposer also ended up getting less money than he would have gotten in an anonymous game while the responder ended up getting more money. And because these games stipulate that in the event that the duo cannot reach a consensus, none of the parties gets the money; the two parties often agreed on a 50 percent share for each person. The results of this type of game seek to shed light on the aspect of utility that is lost when an anonymous bargaining method is employed by two parties who cannot see each other.
Face-to-face interactions call into play a significant proportion of the social training that a person is naturally endowed with. In these types of interactions, there are powerful social motivations that come into play and may significantly affect the whole process (Samuelson, 1998). But when the social behavior, facial expression, and outlook of the other person is not known, responders tend to accept the offers without a word because they do not know the extent of the volatility of the other person’s generosity, enough to reject a proposal; they both need the money. Values such as interpersonal perceptions, prejudices, and incompatibilities among others significantly affect the outcome of the responders and are as such controlled in the anonymous experiments as seen in Ultimatum.
A small degree of change in the social environment can cause large changes in the behavior and perceptions of individuals in a social environment as seen in the low incidences of disagreements that are achieved in the anonymous or controlled bargaining experiments (Schmidt, 2006). Hence it is not in all cases that individuals are motivated by selfish interests as seen in the results of the face-to-face bargaining experiments whereby other motivations are reflected to be derived primarily from the effects of an uncontrolled social environment. These effects are part of what is eliminated in these controlled bargaining environments which further seeks to support the hypothesis that individuals are not purely motivated by self-interest.
There are varying levels of communication that are used by individuals during a bargaining session all of which are lost in a controlled bargaining system. There are various channels of communication that open up as a result of this including the use of cell phones and other methods of non-verbal communication. The use of computer terminals and text messages opens up other channels of communication exempting it from being a purely linguistic channel of communication (Samuelson, 1998). In addition to all these, there are non-verbal methods of communication that are used involving the use of signs, symbols, gestures, and facial expressions among others that are meant to induce certain types of emotions and feelings into the recipient.
The higher levels of disagreement and dissatisfaction occur among those participating in anonymous bargaining due to the restriction of these channels of communication whose absence cannot clearly tell whether the proposer was motivated by self-interest to determine the amount he would give the responder or just whether he did not know who he was dealing with and quoted any figure without the proper facial expression of the responder in mind. Probably in the event of better communication channels, the proposer could have changed his mind and initially quoted a higher figure.
Models of social preference attempt to explain the complexity of the issue depicting that a player may be concerned not only with his own material payoff but with also what the other person is getting be it large or little (Shell, 2006). Hence, the responder may not be willing to accept a certain amount of money but because if he rejects it then both parties lose, he may go ahead and accept the offer knowing too well that they may both lose; better little than none.
Every person has a social preference that in turn affects the allocations of material outcomes (Roth, 1993). These preferences allow this person to achieve a certain level of satisfaction based on some rational or consistent requirements that are focused on the allocation of resources. However, the model of social preference assumes that the person may also care about the resources that are allocated to the other person as a result of several factors. Some people are altruistic; they have the capacity to generate positive utility because they care for the well-being of other people. When a responder perceives the proposer to be generous, then they will also respond in a generous manner; consequently, when they perceive the other party to be mean then they will also react in a meaningful manner (Cruger, 2002).
It thus on this principle that several players determine what type of offers that they should give the other players as this will define whether the offer is accepted or rejected. Hence the aspect of self-interest is challenged in this manner because the person is indeed pursuing self-interest by thinking of ways in which his proposal will not be rejected; so that he can also get money. But at the same time, he is also practicing altruism whereby he has placed the feelings of the other party at the forefront allowing the expression of self-interest to be biased.
In life, individuals are often concerned not only about the amount of money that they are receiving but also about their position relative to those of others; possibly their peers in relation to money (Davis & Holt, 1993). This aspect referred to as relative income is a common cause of jealousy and envy among people all over the world making it a common determinant of some of the actions that people take when broached with the subject of anonymous bargaining.
The subject of relative income is the cause of suffering and self-hate among people who receive less income as compared to their counterparts who receive more in a game. In any situation, one would always wish to get more money than the other person and may not be altogether bothered by losing a little money so as to gain some more in the long run (Bimore, 2002). But the money that he is willing to offer has its own limits so that not too much is lost that cannot be recovered later on. Hence this aspect governs the higher level that the proposer is willing to risk or give to the other player, perceiving the possible amount of money that this player will get and comparing it to his possible profits before he makes a choice on a definite amount.
Inequity aversion is also a common reason why people act the way that they do in a controlled game setting. Most people feel envious beyond control when a person gets material payoffs that are greater in amount as compared to theirs. This can also be used to explain the many reasons why people reject offers given to them by other players opting to settle for a complete loss (Lebow, 1996). Apart from completely diverting the cause of rejection from the theory of self-interest, the aspect of inequity aversion also goes further to explain the reasons why people behave the way that they do and the reasons for the differences in them.
In the event that the proposer quotes a low figure, there are some responders who will go on and accept the quote while there are others who will coldly refuse the offer. It is thus the aspect of equity aversion that allows some people to accept this quote when they perceive that the other player will not gain so much in addition to what they already have and allow others to refuse this quote when they perceive the impossibly huge amounts of money that the other player seeks to gain.
At times, the preferences of one player may be intertwined with those of another player such that the two player’s preferences are interdependent. This is to say that the preferences of one player affect those of another player thus steering the complete course of the game. There are those players that are selfish and then there are those who are generous. If one player possibly the responder knows that the proposer is selfish then he may also adopt selfish tendencies while if he knew that the responder is altruistic then he will be willingly generous in his interactions during the game.
The aspect of intention-based reciprocity also plays a vital role in the approach that a player assumes within these games (Lebow, 1996). A player cares about the intentions of his opponent hence if he feels that the other player’s intention was to be nice to him then it goes without saying that the opponent’s intentions will be received and reciprocated (Davis & Holt, 1993). But if on the other hand, he feels that his opponent had ill and hostile intentions then he may also want to play his opponent by the same rules thus creating a different outcome for the whole game. Hence the perceived intentions of the player are important in determining the path and outcome that the game will realize.
The possibility that some players do care about their opponents is a clear indication of the bias in the self-interest theory that has been stated. Some players may tend to be kinder or more generous with their opponents if they believe that their opponents will also play them by the same rules. They tend to believe that their actions will be reciprocated and are thus more inclined to form beliefs and tendencies which they perceive their opponents will take during the game. Unfortunately, these principles cannot be applied where the second player is involved because it is believed that this second player may not share in the same rules and principles that the first player did. As a result, an offer that may have been gladly accepted by the first player may not be exactly reciprocated by the second player, in the same manner, resulting in a similar offer being accepted and rejected by another player.
The game is also conducted in two rounds that introduce the aspect of the player’s environment into the game. In the first round, the game is players in a real-life setting that allows for the physical distribution of the players into two groups comprising proposers and responders. These groups are then placed separately with communication being carried out through the messenger only. This messenger transfers messages from the proposers in one of the rooms to the responders in the other room. In the second round, the game is played in a less interactive way through a website. Users log into a website in order to register themselves as players after which they are anonymously accorded the role of proposers or responders. Communication between the two takes place through the internet or computer terminal without the presence of a human messenger to transfer the messages from one user to another.
It is thus observed that the offers that are made by the proposers in the first round are slightly higher; an act that can be attributed to the presence of the human messenger. They may perceive that the human messenger will judge them based on the amount that they offer to the responder hence making them more self-aware. This can also be explained through the relatively smaller amounts that are offered by the proposers in the second group. This group takes advantage of the anonymity that these computer terminals offer them to offer whatever amount of money they wish knowing too well that they are not under supervision from anyone. Hence the effects of different social environments can affect the outcome of the game.
Nevertheless, the aspect of reciprocation is foreign to the Ultimatum game because the game is only played once with no chance of the same proposer making an offer to the same responder. This aspect does not give time for the responder to reciprocate the actions of the other player as a result of the one-time contact that the two have. In which case trying to perceive the other player’s actions as an act of reciprocation would not thrive because the two players only have one-time contact.
The issue of acceptance or rejection of an offer can also be explained by the fact that some players feel guilty about accepting or rejecting an order. While some players may feel hurt that they are being cheated during the game, others may feel a sense of responsibility towards the well-being of other people and may not want to hurt their feeling by disappointing them by rejecting their offers. As a result, some people may accept them not based on satisfaction with the offers but as a result of this aspect.
In this case, the people find themselves walking into a room and being divided into two groups after which they are placed in the beneficial room and given free money that they have not worked for. Some people when asked to share this money would feel a certain level of shame and sense of responsibility when they think of offering a small amount of money to the people in the other group. They might probably feel that the messengers within the experiment are watching them and judging them based on their actions during the experiment. It is in such a case that they may be prompted to offer a fair amount of money to the responder as an act of fairness.
Others may just fear rejection, not in the aspect of losing money but along the terms of their offer being rejected by the responder. They would feel a certain level of shame and emotional damage when the responders perceive their offers as too low and a complete shame. Every human being wants to feel needed and appreciated in society and as a result, other people may bank on these types of feelings to play around with their psychology and get what they want (Bimore, 2006)t. It is in this way that the responders; without knowing, get huge offers from the proposers in the other room.
Conclusion
There are several economic implications that are associated with the application of the principles that have been learned from the Ultimatum game into real life. Social subjects who are willing to reciprocate in a business environment are often involved in business deals that present their actions in a manner that demands the other party to reciprocate (Bimore, 2002). This involves the use of generous exemptions; vouchers and attachment to these deals that leave the recipient without a doubt of the extent that the proposer is willing to go to ensure that the business deal pull through.
When a person participates in a market economy, it makes them more selfish driving them more towards the restriction of expenses and maximization of revenue. Nobody in the world has got the emotions, ability, and patience to accept an offer that visibly seeks to deny them of their rights (Lebow, 1996). This is often implemented in managerial situations whereby payment of staff or employees is concerned. Management should have the right mind to realize that people do not often accept to be paid less than they are bringing into the organization and are often ready to tolerate only certain situations when they want the rewards.
Thus, in conclusion, there are several factors that may influence the decision that a person makes during a case whereby they are supposed to share resources like money with another member. It would thus be biased to base these reasons on mere self-interest as a result of the findings of the Ultimatum Game. Individuals are faced with different types of scenarios in which they make decisions that can be analyzed to be as a result of other motivating forces. The external environments within which these people are placed have got a significant contribution to the outcome of their actions and should be carefully considered under such settings.
The strategy is thus useful in corporate environments where managers should look into the various ways that staff can be motivated to increase the revenue that the organization receives. It can also be implemented by public planners to ensure the fair allocation of resources to people within the community and the various types of reactions that can be elicited when such guidelines are not adhered to.
References
Bimore, K. (2002). Game theory and the social contract, Vol 2.Boston: MIT Press.
Cruger, A. (2002). Bargaining theory and fairness: a theoretical and experimental approach considering freedom of choice and the crowding-out of intrinsic motivation. London: Duncker & Humblot, 2002.
Davis, D. and Holt, C. (1993). Experimental Economics. Princeton: Princeton University Press.
Lebow, R. (1996). The art of bargaining. Baltimore: JHU Press.
Roth, A. (1993). Bargaining Experiments. London: Harvester Wheatsheaf.
Samuelson, L. (1998). Evolutionary games and equilibrium selection. Boston: MIT Press.
Schmidt, K. (2006). The Economics of fairness, reciprocity and altruism-experimental evidence and new theories. New York: Elsevier.
Shell, G. (2006). Bargaining for advantage: negotiation strategies for reasonable people. 2nd ed. London: Penguin Books.