Introduction
Gravity throwing machines, or trebuchets, have long been considered a popular engineering invention of the Middle Ages, which were used to throw weapons of war. These weapons could be stones, other heavy objects, or flammable liquids. Trebuchets were first used in China but appeared later in Western Europe (Karlsson 2). The trebuchet should be seen as a more advanced catapult device because this mechanism’s physics allows launching projectiles farther. For this reason, trebuchets began to be used, including not only in the military. However, due to the development of technology in the modern world, gravity-throwing machines are almost not used in military operations.
On the contrary, their range of use today ends at entertainment and academic purposes. In physics and mathematics, they are used to study motion, and in history, they are used to study past human inventions, technological changes, and achievements. The popularity of trebuchets is mainly due to their simplicity: the energy of the sharply falling weight, attached to the short end of the lever, is transferred to the loose core, which due to the resulting momentum, is transported over long distances. Of interest in this context is the relationship between the range of such a throw and the angle of the initial position of the load. The present work investigates how the angle affects the throw range and whether there are any limitations in this connection.
The interest in the study of this paper stems primarily from a personal interest in learning more about the mechanism of medieval invention. It is intriguing how engineers of the Middle Ages could use technology at a primitive level, without digital processing and machine data like today. In addition, personal motivation stems from a desire to test one’s own hypotheses dictated by logical thinking. In particular, it is expected that the higher the angle, the greater the throwing range, but there must be some limitations in this algorithm, which is also of interest to study.
Research Question
What effect does the release angle from the trebuchet mechanism have on the range of the projectile? Additionally, are there any constraints that directly or indirectly affect this relationship?
Variables
The present experimental work investigates the relationship between release angle and projectile range from the trebuchet, and therefore it is possible to postulate which variables are used to study. The independent variable that is manipulated in this work is the release angle of the projectile from the trebuchet. This is a quantitative quantity measured in degrees: a change in the value of the angle is expected to result in a change in projectile range. The dependent variable, in this case, is the range of the projectile. In the absence of other factors, the projectile release angle is expected to have a direct effect on the dependent variable. Finally, the control variables that are not subject to change throughout the experiment are the projectile material and mass, the tribute material, the “weather conditions,” and the measurement scales. In addition, all other characteristics of the trebuchet, except the initial launch angle and the range of the projectile, are also taken as a control variable and do not change throughout the experiment.
Risk Assessment
The estimated risks and methods for dealing with them are summarized in Table 1 below. It should be understood that since the present work is performed in an online format, a simulation is used as the actual experiment, the risks associated with the student’s personal presence in the laboratory are not considered. Nevertheless, some problems could arise during the virtual experiment, which is why Table 1 was used as a risk minimization tool.
Table 1: Risk assessment for the virtual work “Trebuchets Release Angle and Its Effect on Projectile Distance”
Apparatus

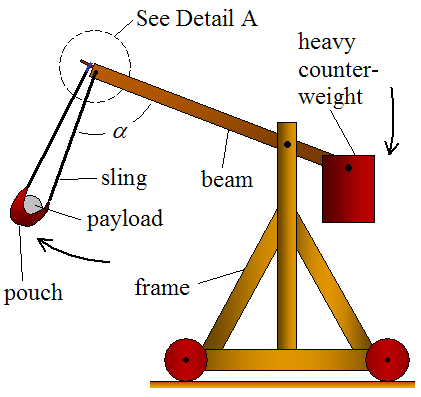
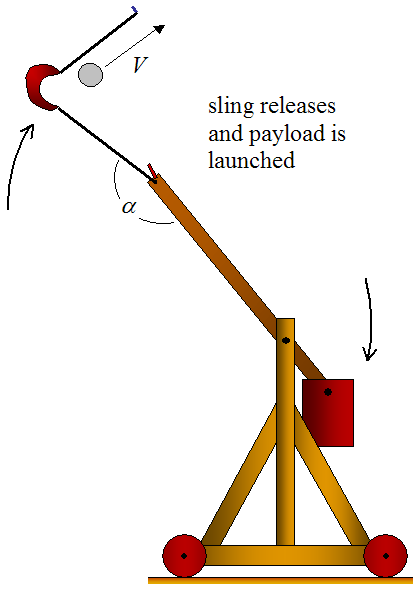
Method
For the present work, the VirtualTrebuchet 2.0 Gravity Throwing Machine Simulator is used to adjust the setup parameters and observe the results manually. This simulator was used to manipulate the launch angle and thoroughly investigate the effect of these manipulations on the throwing range. All of the characteristics of the trebuchet that are not of interest in this paper are rigidly fixed and recorded so that the accuracy of the calculations can be maintained in the event of accidental web page updates. The metric system chosen is meters and kg as SI Units (“SI Units”). Figure 4 below shows the initial parameters that are set for the first run of the Trebuchet: The highlighted fragments are those characteristics that change during the experiment.
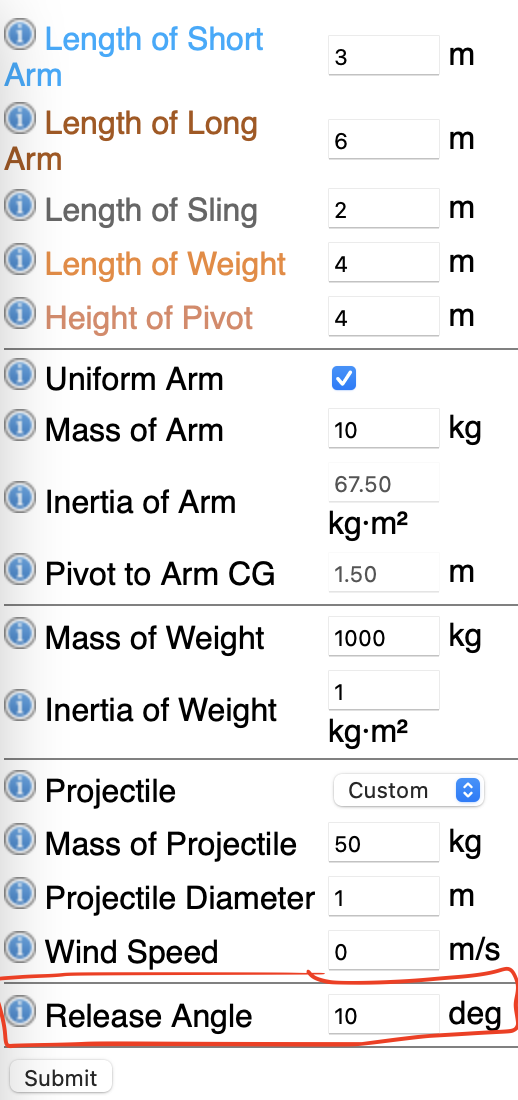
Input Data
The present experiment measures quantitative data that show the dependence of one variable on another. The best format for visualizing such a dependence — the change in throw distance as the release angle changes — is a table. Table 2 below shows the results that were obtained by measuring the throw distance of a 50 kg projectile with a diameter of 1 meter at different angles of release. Note that three measurements for each angle are given to minimize data errors. It is additionally worth noting that the range of angles used ranged from 0° to 80°. The choice of these values is not accidental: beyond these limits in increments of 5°, there are problems of negative distances, which is inappropriate for this measurement.
Table 2: Results of the virtual experiment
Data Processing
The data in Table 2 represent paired numerical regularities, which means that a suitable model for their processing would be the mapping of points on a Cartesian coordinate system. First of all, it should be said that it is impossible to achieve complete unbiased data since all three measurements for each angle give identical results. Apparently, VirtualTrebuchet 2.0 is programmed with equations whose values depend precisely on the input parameters, which means that it is impossible to achieve data diversity. For this reason, averaging and finding mean errors is not possible for this set of numbers. In addition, either a regular linear plot or a regression model can be used, which will predict the results if they have the property of linearity.
Presentation of the Processed Data
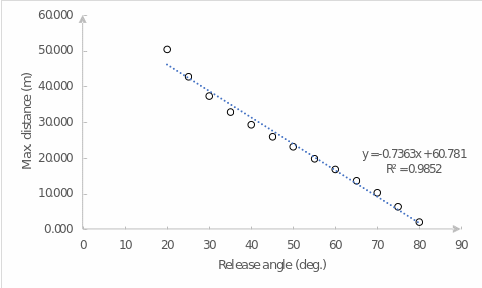
Using MS Excel, a linear plot of the dependence of the throw range on the initial launch angle was constructed. The visualization of this relationship is shown in Figure 5. As can be seen, the graph for the data is not a true straight line but is a curve. In addition, from about 20° on the horizontal axis, an almost strict linear dip begins, which can be described in Figure 6. This Figure clearly shows that the coefficient of determination R2 is critically high and reliably describes the linearity of the decline, but also that if the linear trend were extended to the left, the intersection of the ordinate axis would be at points (0, 60.781). In other words, if there were a strictly linear relationship at all for all angles for the dependence of projectile range on release angle, then at zero, the distance would be maximum. In reality, this is not the case since the relationship does not turn out to be linear, and the maximum projectile duration is peculiar to an angle of 15°.
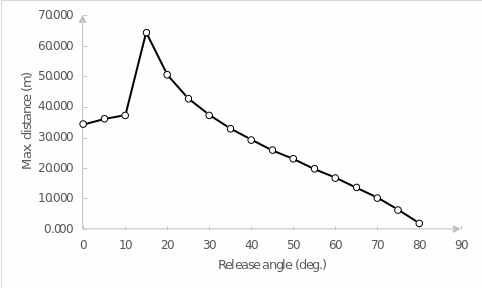
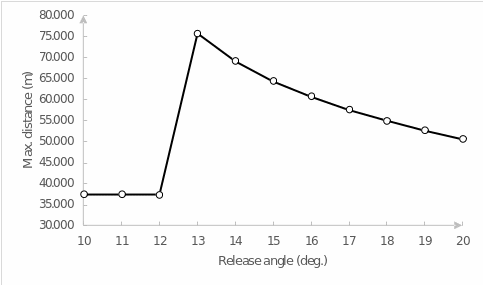
It is interesting to clarify how sensitive this dependence turns out to be when considered in more detail. For this purpose, the interval of release angles from 10° to 20° is considered separately in steps of 1°. Figure 7 reflects this dependence. A closer look reveals that the maximum point for the range is not 15°, as previously thought, but 13°: in this case, the projectile throwing range was 75.677 meters. In addition, another intriguing detail becomes noticeable: the tendency for the range drop after the maximum can be described not only as a linear function but apparently as a parabola due to the smooth, slower drop than in the case of the linear graph.
Conclusion
In summary, it must be drawn several important conclusions about the trends found in the data processing of this experiment. First, the throwing range of the projectile directly depends on the initial release angle from the rig. Second, this relationship is not wholly linear or described by another simple function: on the contrary, the overall graph of the relationship is a broken curve. Third, the range of the projectile can be affected by the characteristics of the trebuchet, which were not considered in this paper and were taken as control variables. Fourth, for a more accurate result, i.e., to find the angle contributing to the maximum range, it is necessary to investigate the peak region of the function in more detail. Fifth, the period after the maximum is a decline, and this decline can be described either by linear regression or as a quadratic function.
Estimation
In fact, the data obtained should agree well with the theoretical data obtained using known formulas. Thus, it is a reference to find the initial velocity of the projectile using the following equation (Cwiakala):
At the same time, the formula for finding the maximum distance:
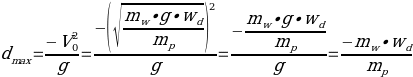
Consequently, for the experimental data, the maximum throw distance will be equal to:
However, the maximum throw range at a 1° step in this experiment was 75.677. It is likely that the true angle at which the range will be 80 meters is not an integer value. An estimate of the absolute and relative error for these measurements is then:
Thus, the calculation error does not exceed 5.4 percent, which is a comparatively good result for a non-sensitive measurement of the maximum throw distance.
Improvement
In future iterations of this or similar work, it is recommended to use a more accurate, systematic scale for measurement. Instead of randomly selecting a step of degrees, off-the-shelf software can be used for a more accurate measurement: it can be an interval with steps as small as 0.01°. This sensitivity is supposed to give more reliable results and reduce the error. In addition, for future works it is suggested to complicate the study design and to measure the effect of several independent variables on the final result. In addition to the release angle, this could be the length of the short arm of the lever or the mass of the projectile as additional characteristics affecting the variable.
Works Cited
Cwiakala, M. “Trebuchet Maximum Distance”. Swift Calcs, 2018, Web.
Karlsson, Daniel. “The Trebuchet: Longer Shots with Wheels?”. 2018, pp. 1– 21, FYGB08. Web.
“SI Units.” NIST, 2021, Web.
“Trebuchet Physics”. RPWP, Web.
“Unleashing a Medieval Trebuchet on a Wooden Palisade”. YouTube, uploaded by Smithsonian Channel, 2020, Web.