Typical Reasonably Homogeneous Equilibrium in Water Report

Introduction

The dispersion of molecules of iodine 1² between immiscible liquids solvents, water, or carbon tetrachloride was used to estimate the molarity of the 1² substances involved at balance in the aqueous solution. The lack of information regarding activity coefficients for any complexes present complicates the investigation. Early scientists recognized the necessity to assume equal degrees of solubility for -iodide and polyiodide salts.

It is important that the diffusion coefficient used to link the iodine concentrations in one phase to that in another account for the existence of iodide and polyiodide salts. The distribution coefficient must also account for or reduce iodine hydrolysis. Even while polyiodides are undeniably present in solid form, the presence of an Ig-KI molecule in solution is uncertain. The water chemistry of Iodine has been studied at a variety of pH, concentrations, and temperatures to understand how this fission product behaves in accident circumstances. Notable about equilibria is that both forward and backward processes persist. Their rates are identical; thus, any change in one response is cancelled out by the other. Chemical equilibrium is dynamic, not static. Because both reactions occur at the same time, the equilibrium may be reversed. Using an equilibrium as an example,

represents the same equilibria as:

Iodine interacts with iodide ions, which may serve as Lewis bases, increasing its solubility in water. By adding cesium iodide, the reddish-brown solubility becomes crystalline cesium triiodide.

In preparative chemistry, it is often required to extract the desired product from a chemical mixture into a more soluble liquid than the undesirable components. On a laboratory scale, this is done in a separatory funnel. Pour the two or more substances into the funnel via the top hole. The funnel is shaken to mix the two stages, then put aside to enable the layers to form. The iodine complex is a polyiodide system. It was researched longer than iodine reactions. Because little is known about starch and aqueous solutions containing Iodine and iodide, less is known about the starch-iodine reaction. Multiple sources describe varying levels of reaction.

Purpose

This experiment was designed to examine a typical reasonably homogeneous equilibrium in water and test the law of mass action. Equilibration happened when Iodine was combined with aqueous potassium iodide solutions: 1²+1 = 1. (1) It is used to redistribute natural Iodine I between two immiscible solvents, water, and methylene chloride, to determine the equilibrium concentrations of the 1² species present in the aqueous solution. This experiment compares the solute distribution in the aqueous phase and CC14. It connects the concentration of 1² in two stages (12) and (I2) CCU.

Experimental

Reagents

• Distilled water (200 ml)
• Solutions of 1₂ in CCI₄ (50 ml)
• CCL4 solvent
• Pure H₂O
• H2
• Solutions of I² in CCI₄
• Aqueous S₂O₃^2-
• Aqueous KI

Instrumentation

• Clamp
• Battery jar containing water at 25°
• a pipette bulb
• Thermostat bath
• 500-ml glass-stoppered Erlenmeyer flasks.
• Pipettes

Chemical Formulas

The equilibrium conditions constant Kg, which must be stated in terms of the process of the different molecules involved, is approximated by the following equation involving concentrations: A are activities, y are activities coefficients, and K is the equilibrium constant to maintain optimally. (X) = Cyclo, in which CCL₄ is the number of moles of chemical X while co = 1 M.

K, = K comes from y = y and Yi, = 1. The estimated Debye-Hickel theory for ionic species activity coefficients at 25°C is! -0.507z? Y = – (3) +1 With the correctness of Eq., both l^o and I^z have the same charges z and are affected by the same ionic strength 1. (3).

Procedure

1. 50 ml 12 in CCI4 solutions was placed in 500 ml crystal Erlenmeyer flasks and allowed to equilibrate at 25°C.
2. The flasks holding the solutions were shaken thoroughly for 5 minutes before clamping them in a thermostatic bath.
3. After ten minutes of temperature equilibrium, the flasks were taken one by one and wrapped in a clean towel
4. The flasks were aggressively shaken for three to five minutes and then replaced in the thermostat bath. This process was repeated for at least eight hours.
5. After the last stirring, the flasks were placed in the boiling water bath to enable the fluid layers to completely separate. After full equilibration, one flask was removed from the thermostatic bath then placed in a battery jar loaded with 25°C water.
6. Pipettes were used to extract a sample of the aqueous layer or a portion of the CC14 layer. The flask was capped and reintroduced to the solution for a further 30 minutes of equilibrium with shaking as stated before, followed by a second specimen of each stage for titration.

Results and Discussions

Results And Calculations

Results and Calculations for:

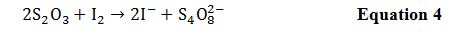
Aqueous Calculations for Phases 1,2,3

Table 1

Calculations for phases 1, 2 and 3 can be done as follows:

CCL4 calculations for phases 1,2,3.

Table 2

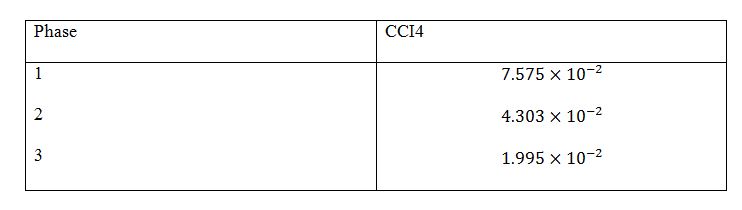
Calculations for:

Table 3

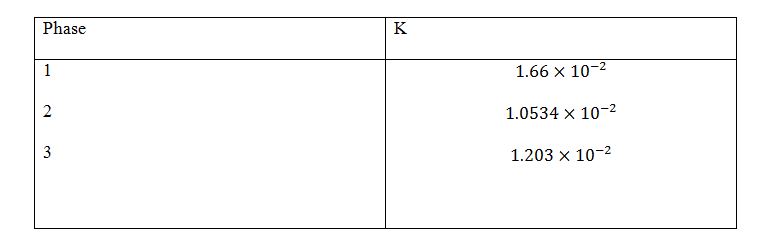
The calculations are done as follows:

Calculations for Phases 4,5 And 6.

Table 4

Table 5

Discussions

At equilibrium, the rate of forwarding reaction matches the rate of the reverse reaction. Chemicals in equilibrium have a constant concentration. No matter how many times a reactant molecule becomes a product molecule or vice versa, the reactant and product concentrations are maintained at the same level. It is 0 at equilibrium. Neither a forward nor a backward response is natural. Observe the ice-water shift. Above 0°C, ice spontaneously melts into liquid water; G is negative. G is positive when the ice melts below 0°C. At 0°C, both states are equal.

The quantity of ice and water in the combination remains constant, and the change in entropy is zero. A rising concentration of reactant solution causes a change in the generation constants of triiodide, but why? To begin with, iodine and iodide ion interactions in mildly concentrated solutions produced higher-order complexions. The experimental data is contradictory and typically relates to solids instead of aqueous solutions. The assumption that species in solutions have the same complex as those in solids has led to a lack of interest in studying them. It is important that the diffusion coefficient used to link the iodine concentration with one phase to that in another account for the existence of iodide and polyiodide salts. The distribution coefficient must also account for or reduce iodine hydrolysis. Because of the fast and reversible equilibrium, it isn’t easy to estimate the proportion of Free Iodine in quite an Aqueous Phase with a Significant Amount of Iodide Ions by Direct Titration. In such systems, one must use an indirect approach to determine free Iodine.

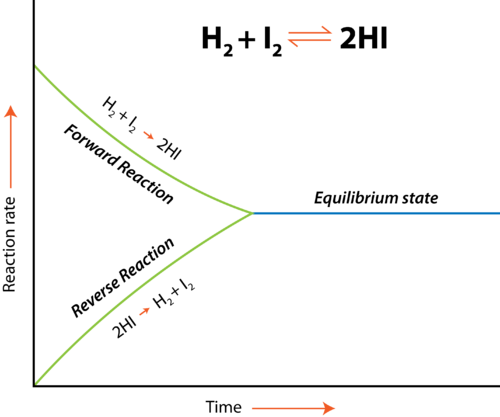
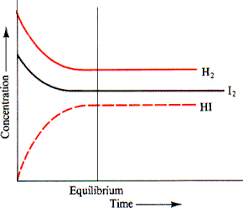
The amount of an empirical formula is unrelated to the method used to achieve equilibrium. The H2 + I2 2 HI equilibrium is characterized by the following data. It illustrates many distinct starting concentrations and their associated equilibrium concentrations. Each experiment includes information on the equilibrium constant. Notably, the equilibrium constant remains constant regardless of whether the particles were hydrogen and iodine, the hydrogen iodide molecule, or a mixture of all three, regardless of whether the constituents were mixed insufficient or unequal quantities.

Like Henry’s rule, this distribution law only applies to a particular chemical species. This indicates that the distribution variable k is not a natural thermodynamic equilibrium constant. Due to the comparatively high concentration for 12 in the CC14 phase, it is prudent to calculate kat various concentrations. When 12 is dispersed between CC14 and plain water, it may be measured immediately by titration. To produce (I2) in an aqueous solution containing 13′, titrate the 12 in a CCI4 layer equilibrated with this phase. The assumption is that the existence of ions in the aqueous solution phase does not affect the distribution constant’s value.

However, a more fundamental problem arises in that the identities of the complexes apart from triiodide that may occur in aqueous systems are unknown. Until the composition of these complexes is determined, no progress toward a quantitatively satisfying description of these solutions can be achieved. In light of a few good descriptions of pentaiodides, hepta-iodides, and sometimes even pentaiodides in the research, it has been implicitly believed that the ions found in solution are of the same general kind.

Summary

The formation of the triiodide ion (I3) in aqueous systems iodine and iodide is well known. Additionally, these solutions include more complex polyiodide ions. However, it is unknown what additional ions are produced in addition to I3. Along with more complex ions, ions of the types I⁴ 2, I⁵ 2, and I⁶ 2 have been suggested. When a third material that is soluble in liquids is introduced to a system comprising two immiscible liquids, the component disperses uniformly across the two liquid phases. For practical reasons, this precise formulation of the dispersion law may be approximated. If the solutions behave optimally to use Henry’s or Raoult’s Laws, the activity may be substituted by the relevant mole fractions. It is widely known that in the presence of starch, solutes of Iodine may take on a vivid blue hue. For over 150 years, the complex identified as responsible for this absorption coefficient of a red signal has focused on intermittently intensive investigation. Nonetheless, as with the creation of a poly iodine complex in starch, the underlying nature of the process that produces this blue complex is only partially known.

References

Garland, Nibler, & Shoemaker. Exp. 5: Chemical Equilibrium in Solution. Experiments In Physical Chemistry.