Abstract
This paper proposes a lightweight image encryption scheme based on three stages. The first phase incorporates the use of the Rössler attractor for the Rössler system; the second stage includes the usage of a PRNG S-Box, while the third stage concerns the implementation of the Recaman’s Sequence. The performance of the proposed encryption scheme is evaluated by implementing pre-determined metrics. The metrics’ computed values indicate a comparable performance to counterpart schemes from the literature at a meager cost of processing time. Such a trait suggests that the proposed image encryption scheme possesses the potential for real-time image security applications.
Introduction
The tremendous evolution in digital image processing and network communications has created an extensive demand for real-time secure image transmission over the Internet and through wireless networks. From these considerations, data security in cryptography and steganography has become a vital means to ensure safe operations and the usage of millions of online applications. Cryptography, which plays a critical role in information security, has captured the attention of scientists and engineers with its contribution to research in recent decades. Furthermore, the current studies focus on refining the security of image transmission. For instance, new cryptosystems, including the cellular automata and chaos, have been proposed. Chaos is characterized by pseudo-randomness, ergodicity, and high sensitivity to initial conditions and parameters, so it is extensively used in image encryption schemes. The outcomes of the described approaches have commonly involved the usage of one or more PRNGs, as well as true RNGs. The literature incorporates examples of pooling chaos theory, Recaman’s sequence, electrical circuits, quantum physics, and many others.
The Rössler system is a third-order continuous-time system with a single quadratic cross-term and depends on three parameters originally introduced by Otto Rössler in the 1970s. These differential equations create a continuous-time dynamical system that calculates chaotic dynamics associated with the fractal properties of the attractor. The calculated characteristics commonly concern the generation of a single lobe chaotic attractor (spiral-type) following a period-doubling cascade of a limit cycle or a more complicated chaotic attractor (screw-type) due to the presence of homo-clinic orbits. Some properties of the Rössler system can be derived from linear methods such as eigenvectors; however, the system’s main features require non-linear processes, such as Poincaré maps and bifurcation diagrams. The original Rössler paper stated that the Rössler attractor was designed to operate similarly to the Lorenz attractor; moreover, it was also easier to analyze qualitatively.
An S-Box (substitution-box) is a fundamental component of symmetric key algorithms that perform the substitution process in cryptography. In block ciphers, they are typically utilized to obscure the relationship between the key and the cipher text, thus, ensuring Shannon’s property of confusion. The first S-box is used on symmetric key algorithms, such as Advanced Encryption Standard (AES) and the Data Encryption Standard (DES); however, one of the primary concerns of the described S-boxes is the statistic behavior. Therefore, PRNG and Chaotic systems are implemented to assemble an S-box and produce dynamics. The authors of introduced a novel approach to constructing S-boxes based on the Rössler system and demonstrated the approach’s effectiveness against extensive attacks.
The Recaman’s sequence is an impressive sequence of integers that are simple to define; however, the ultimate complexity exhibits how effective it can be against cryptanalysis. The authors of used Recaman’s sequence image steganography for 2D images, demonstrating the extensive results of the proposed scheme.
Ultimately, the current paper proposes an image encryption scheme based on three consequent stages. The first phase incorporates the usage of the Rössler system, the second stage concerns the construction of an S-Box, and the third stage emphasizes the usage of the Recaman’s Sequence. The current paper has the following structure: Section II briefly presents the overview of the Rössler system, PRNG S-Box, and the Recaman’s Sequence used for the proposed image encryption scheme. Consequently, Section III outlines the numerical results of the computations and testing and provides appropriate commentary on them. Ultimately, Section IV concludes the paper and proposes a direction for future work.

The Proposed Image Encryption Scheme
As mentioned briefly before, the proposed image encryption scheme is comprised of three stages. The first stage utilizes the Rössler system; the second phase concerns the construction of the PRNG substitution box (S-Box); the third stage emphasizes the Recaman’s sequence. The following sections introduce each concept and provide a brief overview of the systems.
Rössler Attractor
The Rössler system is a widely spread prototype of a continuous dynamical system defined by the following set of three nonlinear equations:
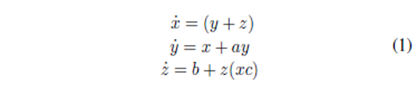
where a, b and c are non-negative parameters. The system approaches chaos through a period-doubling bifurcation route.
In our encryption scheme, the used parameter values are: a = 0.1, b = 0.01, and c = 14, resulting in the chart demonstrated in Fig. 1. A 2D representation for Rössler attractor points are shown in Fig. 2.
S-Box
A substitution box is a pivotal constituent of modern-day block ciphers that assists in the transformation of a disorderly cipher text into the specified plain text [19]. Incorporating the S-box, a nonlinear mapping among the input and output data is established to create confusion. Thus, the security of data relies on the substitution process. Substitution is a nonlinear transformation that performs confusion of bits. It provides the cryptosystem with the confusion described by Shannon. An S-box generally takes m input bits and transforms them into n output bits. The system is called an mn S-box and is often implemented as a lookup table. These S-boxes are carefully selected to resist and obstruct linear and differential cryptanalysis. Thus, incorporating an S-box, a nonlinear mapping among the input and output data is established to create confusion.
A simple and efficient technique for S-box construction, using the idea of novel transformation, modular inverse, and permutation, was inherited from the authors of, where an example of an S-box was evaluated and analyzed to verify its cryptographic forte using standard criteria. Consequently, its performance was examined by comparing it with other recently projected S-boxes. The research has demonstrated extensive results that meet the requirements of the benchmarks, which validate the implementation of the technique. Furthermore, the investigation transparently indicated the high efficiency of the proposed S-box by comparing it with analogs.
In our encryption scheme, we used a randomly generated s-box with a 16×16 dimension, the values of which can be seen in Table IV.
Recaman’s Sequence
In order to generate the Recaman’s sequence, we assume that a1 = 1 and follow the mathematical form demonstrated below:
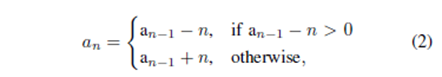
where n is the position of the element in the sequence.
Fig. 3 is the 2D graphical representation for the first 200 iterations, which were used in our proposed encryption scheme to generate a key of random bits.
Image Encryption and Decryption Processes
The proposed image encryption scheme is implemented following the structure below. First, an image of appropriate dimensions is chosen, and its pixels are converted into a 1D stream of bytes. Consequently, these bytes are converted into a bit stream d. Secondly, the mean intensity of the image pixels is calculated. The resulting value is a relatively small number, which we multiply by a magnifying factor fM. Let us denote the resulting value by μ. Next, we cyclically shift d to the right by μ places and the resulting bit stream, now denoted dμ, is then XORed with kCA. kCA is the first key, a bit stream of the same length as d and dμ, consisting of a repetition of the first NCA bits resulting from the binary representation of the first 250 Rössler numbers in the Rössler attractor. Lastly, we denote the resulting bit stream as C1, which concludes the first step of the encryption.
For the next step, we utilize the S-box to substitute the decimal representation for every 8 binaries from the stream of binaries acquired after the first step as in Table IV. Consequently, we change those decimal representations to a bit stream C2. At this point, we apply the x and y coordinates of each of the points to the Recaman’s Sequence equations and flatten them into a single 1D array. Next, we list plot the mentioned values into 2D, as demonstrated in Fig. 3. Examining the plot in Fig. 3, we change those integer values to binaries.
These newly obtained bit streams of length NL would make up the seed of our Recaman’s Sequence based key. We repeat those NL bits until they are of the same length as d and C1, thus forming the second key, denoted as kL. Consequently, we XOR kL with C2 obtaining C3, which concludes the third step of the encryption. Ultimately, C3 is reshaped back into an image of the same dimensions as those of the plain image, obtaining the encrypted image. The decryption process is implemented in a reverse manner as to that of the encryption process.
Numerical Results and Performance Evaluation
The current section outlines the numerical results of the proposed lightweight image encryption scheme. Performance is evaluated and compared to counterpart algorithms found in the literature. The proposed scheme is implemented using the computer algebra system Wolfram Mathematica® with a machine running Windows 10 Enterprise, equipped with a 2.3 GHz 8-Core Intel® CoreTM i7 processor and 32 GB of 2400 MHz DDR4 of memory. The utilized keys are assigned thefollowing values: NCA = 250, NL = 200, fM = 106, and λ = 10. Four images commonly used in image processing applications/experimentation are utilized in this section. These are Lena, Mandrill, Peppers, and House with the dimensions of 256 × 256.
Fig. 4 demonstrates the correlation of the plain and encrypted Lena image coefficient diagrams. It is transparent that the horizontal, vertical, and diagonal correlation coefficients of the adjacent pixels for the plain image are linear. However, the inspection of the plots generated from the encrypted image demonstrates that the plots are uniform and have a scatter-like distribution. This notion signifies the resistance of the proposed scheme to statistical analyses or attacks.

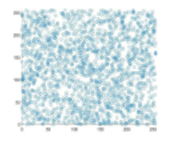
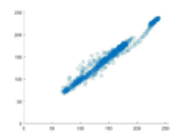



Table III lists the computed values of MSE and PSNR of our proposed scheme, as well as its two counterparts from the literature. A more significant value of the MSE signifies an improved level of security. Our proposed schemes seem to outperform the MSE values of, but achieve a lower performance than the one demonstrated in . Since the PSNR is an inversely proportional metric to the MSE, the comparison among the three schemes in terms of PSNR still holds the same significance as mentioned before.
Conclusion and Future Works
In this paper, we proposed an image encryption scheme based on three consequent stages. The first stage incorporated the usage of the Rössler System; the second phase implemented the construction of a PRNG S-Box; the ultimate stage concerned the usage of the Recaman’s Sequence. Performance evaluation of the proposed scheme was carried out utilizing several appropriate metrics and analyses, including visual inspection of both plain and encrypted images, a histogram analysis, a cross-correlation analysis, the inspection of entropy values, and computation of the MSE and the PSNR values. Consequently, we compared the proposed image encryption scheme with its counterpart methods from the literature, demonstrating the comparable security performance of the proposed system. Ultimately, the research provides evidence for low processing time, signifying the practicality of the method and its potential usage in real-time applications. Future work is expected to result in improved performance and should include the implementation of another substitution phase between the two proposed stages of image encryption.
References
A. El Mahdy and W. Alexan, “A threshold-free llr-based scheme to minimize the ber for decode-and-forward relaying,” Wireless Personal Communications, vol. 100, no. 3, pp. 787–801, 2018.
M. I. Mihailescu and S. L. Nita, “Big data cryptography,” in Pro Cryptography and Cryptanalysis. Springer, 2021, pp. 379–400.
W. Alexan, M. El Beheiry, and O. Gamal-Eldin, “A comparative study among different mathematical sequences in 3d image steganography,” International Journal of Computing and Digital Systems, vol. 9, no. 4, pp. 545–552, 2020.
W. El-Shafai, I. M. Almomani, and A. Alkhayer, “Optical bitplane- based 3d-jst cryptography algorithm with cascaded 2d-frft encryption for efficient and secure hevc communication,” IEEE Access, vol. 9, pp. 35 004–35 026, 2021.
I. Verbauwhede, “The cost of cryptography: Is low budget possible?” in 2011 IEEE 17th International On-Line Testing Symposium, 2011, pp. 133–133.
G. De Meulenaer, F. Gosset, F.-X. Standaert, and O. Pereira, “On the energy cost of communication and cryptography in wireless sensor networks,” in 2008 IEEE International Conference on Wireless and Mobile Computing, Networking and Communications. IEEE, 2008, pp. 580–585.
H. Rifa-Pous and J. Herrera-Joancomart´ı, “Computational and energy costs of cryptographic algorithms on handheld devices,” Future internet, vol. 3, no. 1, pp. 31–48, 2011.
K. M. Hosny, Multimedia security using chaotic maps: principles and methodologies. Springer Nature, 2020, vol. 884.
S. Wolfram, A new kind of science. Wolfram media Champaign, IL, 2002, vol. 5.
C. Wen, X. Li, T. Zanotti, F. M. Puglisi, Y. Shi, F. Saiz, A. Antidormi, S. Roche, W. Zheng, X. Liang et al., “Advanced data encryption using 2d materials,” Advanced Materials, p. 2100185, 2021.
Y. Zhang, H.-P. Lo, A. Mink, T. Ikuta, T. Honjo, H. Takesue, and W. J. Munro, “A simple low-latency real-time certifiable quantum random number generator,” Nature communications, vol. 12, no. 1, pp. 1–8, 2021.
O. Rossler, “An equation for hyperchaos,” Physics Letters A, vol. 71, no. 2-3, pp. 155–157, 1979.
O. E. R¨ossler, “An equation for continuous chaos,” Physics Letters A, vol. 57, no. 5, pp. 397–398, 1976.
R. Genesio, G. Innocenti, and F. Gualdani, “A global qualitative view of bifurcations and dynamics in the r ¨ossler system,” Physics Letters A, vol. 372, no. 11, pp. 1799–1809, 2008.
G. Wang, “Chaos synchronization of discrete-time dynamic systems with a limited capacity communication channel,” Nonlinear Dynamics, vol. 63, no. 1, pp. 277–283, 2011.
G. Alvarez, F. Montoya, M. Romera, and G. Pastor, “Cryptanalysis of a discrete chaotic cryptosystem using external key,” Physics Letters A, vol. 319, no. 3-4, pp. 334–339, 2003.
A. Belazi, R. Rhouma, and S. Belghith, “A novel approach to construct s-box based on rossler system,” in 2015 international wire- less communications and mobile computing conference (IWCMC). IEEE, 2015, pp. 611–615.
S. Farrag and W. Alexan, “Secure 2d image steganography using Recaman’s sequence,” in 2019 International Conference on Advanced Communication Technologies and Networking (CommNet). IEEE, 2019, pp. 1–6.
M. F. Khan, A. Ahmed, and K. Saleem. “A novel cryptographic substitution box design using Gaussian distribution,” IEEE Access, vol. 7, 2019, pp. 15999-16007.
M. Ahmad, H. Chugh, A. Goel, and P. Singla, “A chaos based method for efficient cryptographic s-box design,” in International Symposium on Security in Computing and Communication. Springer, 2013, pp. 130–137.
V. M. Silva-Garcia, R. Flores-Carapia, C. Renteria-Marquez, B. Luna-Benoso, and M. Aldape-Perez. “Substitution box generation using Chaos: An image encryption application,” Applied Mathematics and Computation, vol. 332, 2018, pp. 123-135.
C. E. Shannon, “Communication theory of secrecy systems,” The Bell system technical journal, vol. 28, no. 4, pp. 656–715, 1949.
E. Tanyildizi and F. Ozkaynak, “A new chaotic s-box generation method using parameter optimization of one dimensional chaotic maps,” IEEE Access, vol. 7, pp. 117 829–117 838, 2019.
M. Ahmad, E. Al-Solami, A. M. Alghamdi, and M. A. Yousaf, “Bijective s-boxes method using improved chaotic map-based heuristic search and algebraic group structures,” IEEE Access, vol. 8, pp. 110 397–110 411, 2020.
A. H. Zahid, E. Al-Solami, and M. Ahmad, “A novel modular approach based substitution-box design for image encryption,” IEEE Access, vol. 8, pp. 150 326–150 340, 2020.
M. Khan and F. Masood, “A novel chaotic image encryption technique based on multiple discrete dynamical maps,” Multimedia Tools and Applications, vol. 78, no. 18, pp. 26 203–26 222, 2019.
I. Younas and M. Khan, “A new efficient digital image encryption based on inverse left almost semi group and lorenz chaotic system,” Entropy, vol. 20, no. 12, p. 913, 2018.