Introduction
The chapter introduces the neural network, which is a massively parallel distributed processor constituted of simple processing units with a natural propensity for storing experiential knowledge and availing it for use. The neural network resembles the brain in two ways. The first one is the acquisition of knowledge by the network from its context via a learning process. The second one is the strengths of connection for the interneuron known as synaptic weights. They are utilized in the storage of learned information. The human nervous system consists of a three-stage system constituting receptors, a neural network, and effectors. The main task of receptors is to modify stimuli of any nature into electric compulsions, which carry the information to the brain. On the other hand, the main objective of effectors is to change the electric compulsions, which the neural network creates into apparent responses as a way of establishing the system outputs. The neural net contains more than 100 billion neurons. The main components of the central nervous system are the brain and spinal code.
The brain has interregional circuits, constituting pathways, columns, and topographic maps. Local circuits are approximately 1mm in size and contain neurons with varied or the same properties. Neurons are approximately 100 microns with the dendritic as the subunits. A neural microcircuit is an assembly of the synapses created in a pattern of connectivity in order to produce a functional operation of interest. Due to their smallest size, they are measured in microns with the fastest speed of milliseconds. Synapses are the most basic aspect because they depend on molecules and ions to enhance their actions. The sensory inputs include motor, visual, somatosensory, and auditory, among others. They are mapped onto the corresponding regions of the cerebral cortex in patterns. The following video illustrates the adaptability of the human brain to its functions. The models of a neuron refer to the artificial neurons developed to study the real neural networks of the brain. The design uses extensive mathematical models to develop a structure for human brain architecture to study the central nervous system.
Lecture
The main objective of the perceptron is to perform correct categorization of the internal stimuli sets given as X1, X2,…………X m into either of the classes C1 or C2. The classification is made through a decision rule that assigns the point represented by X1, X2 …X m to class C1 if the output of the perceptron, y = +1, and to class C2 if the output of y = -1. The hyperplane is a technique used in making the decision boundary for the two-dimensional categories. The hyperplane applies the following formula in classification:
Class 2:
Class 1:
The above formula is a linear equation that produces a straight line with a negative gradient. The perceptron convergence theorem is a framework used to develop an understanding of the error-correction that applies the perceptron algorithms. It uses the signal-flow graph model and applies the following equation: x(n)=[+1, x1(n), x2(n),…, MX(n)]T and w(n)=[b, w1(n), w2(n),…, wm(n)]T. A linearly separable data shows the existence of weight vector, w and, hence, WTX> 0 for each input vector X for Class 1. The next technique is the perceptron and two-class Bayes classifier. It is used to determine the class of an observation denoted by x. The observations are determined either as Class 1, or Class 2 categories.
However, to minimize the average risk or cost, a classifier is created. In the case of the Bayes Classifier for a Gaussian distribution, the mean of X varies from one class to another with the same covariance matrix in both classes. The equations for the classes are E[ X ]=μ1, E[( X −μ1)( X −μ1)T ]=C and E[ X ]=μ2, E[( X −μ2)( X −μ2)T ]=C. The Bayes classifier of a Gaussian distribution takes the form of Rosenblatt’s perceptron when the covariance matrix of X is similar for both classes. The linearly separable classes have perceptron that gives a perfect classification. Nevertheless, Gaussian distribution intersects and is not linearly separable. As the classification error takes place in most cases, the main objective is to minimize the risk.
Multilayer Perceptron
In a network layer, a neuron is connected to all other neurons in the previous layer. The flow of the signal in a network occurs in the forward direction. The multilayer network has two kinds of signals, which are functional signal and error signal. A functional signal refers to input or stimulus, which comes through an input end of the network and propagates from one neuron to another through the network. The signal then emerges into the other end of the network as an output network. On the other hand, the error signal comes from the output end and propagates in the opposite direction. It is called theerror signal’ as its computation depends on errors.
The error energy refers to the training set denoted by T, which constitutes a set of inputs denoted by X(n) and output denoted by d(n) for the neural network.

Back propagation can be explained in two cases. The first case is when the neuron j makes the output node. In this case, the needed response is identified as ej(n) = dj(n)-yj(n). The second case is when the neuron j makes the hidden node and the needed response is unknown. In this case, the error signal should be evaluated in a recursive manner as it works backward. The calculation of the local gradient for every hidden neuron is done using the following equation:
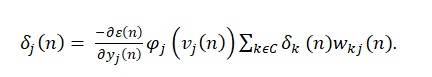
It is possible to adjust layer by layer the weights, which connects every neuron I to neuron j using the following expressions:
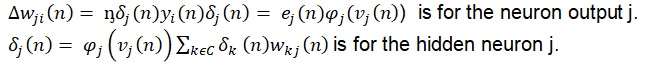
The local gradient of the neuron j as an output is equal to the product of the derivative and the error of the activation function. The local gradient for the hidden neuron is equal to the product of the derivative’s activation function and the next layer’s weighted sum of every calculated local gradient for the neurons. There are two passes of calculation, which are forward pass and backward pass. The forward pass calculates the activation function derivative for the neuron and all errors of output layer. In terms of backward pass, the local gradients of the output layer neurons are calculated first before calculating the local gradients of the hidden layer neurons. When the learning rate parameter η is small, the network experiences change in the synaptic weights with smooth transition and slower learning rate. The increase of η will increase the speed of the learning with oscillatory network weights. Increasing the learning rate helps in avoiding the dangers associated with the instability. This is achieved by including a term for the momentum. In summary, the back-propagation algorithm is done in five steps, which are initialization, presentation of training examples, forward computation, backward computation, and iteration.
In terms of XOR Problem, we refer to the single-layer perceptron developed by Rosenblatt, which cannot classify the non-linearly separable input patterns. In this case, a multi-layer perceptron is necessary for non-linearly separable patterns. The cross validation is used to train the artificial neural network to learn much about the past in order to generalize to the upcoming events. This is achieved through the random partition of training sample. The convolution neural network is enhanced in the modern context using advanced computation system. The system is used to analyze the output layer and the hidden layer of neuron network.
Performance Surfaces
An artificial neural network denoted by ANN constitutes weights and biases. These components are ideally determined in a way that minimizes the output. In this sense, the output error is viewed as a function of weights and biases. This can be expressed in terms of Taylor’s series as shown in the equation below:
F(x) = e-x = e-0 – e-0(x -0) + ½ e-0(x-0)2 – 1/6 e-0 (x – 0) 3 + …
F(x) = 1 – x + ½ x2 – 1/6 x3 +…
Taylor series approximations are as follows:
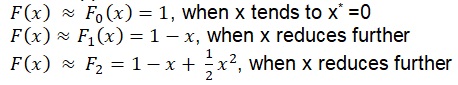
, when x reduces further.
Taylor series can also be used in Vector Case when there are multiple variables in which F as a function of x is given by the following equation:
F(x) = F(x1, x2,… xn).
Vectors and a matrix can be used to represent a multiple variable in the second order Taylor series expansion as shown in the equation below:
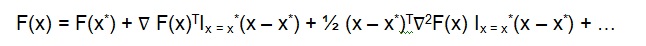
The first gradient or derivative of F(x) along xi axis is given by ∂F(x) / ∂xi , which is the ith element of gradient. The second derivative is a curvature of F(x) along the axis of xi is given by ∂2F(x) / ∂x2i , which is I element of Hessian. The first derivative for F(x) is the projection of slope onto the direction of p and is given by
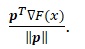
The second derivative of F(x) is the curvature along the vector p and it is given by
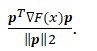
There are three types of minima, which are strong minimum, global minimum, and weak minimum. Strong minimum of F(x) occurs at point x* when a scalar ∂>0.
When there are positive eigenvalues of the Hessian matrix, then the function given will have a single strong minimum. On the other hand, a single strong maximum is achieved with all negative eigenvalues of the Hessian matrix. A single saddle point is achieved when there are both positive and negative eigenvalues. A weak minimum or lack of stationary point occurs when some eigenvalues are zero but with nonnegative values. Weak maximum with no stationary point occurs when the eigenvalues have some zero values without positive ones.
Performance Optimization
The analysis of the basic optimization algorithm can be achieved using the following equations. These are:
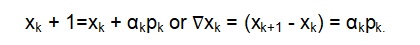
In this case, pk is the search direction, while the αk is the vector. To determine the Steepest Descent, the next step is chosen for the function to decrease by F(xk+1) < F(xk). For small changes in the value of x, the F(x) can be approximated as follows:
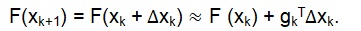
To decrease the function, we used the following equation:
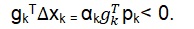
The decreased function can be maximized by choosing pk = -gk. This gives the following expression: xk + 1 = xk – αk gk.
A stable learning rate, also known as quadratic, is achieved using the following equations:
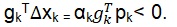
F(x) = ½ xT A x + dT x + c
F (x) = A x + d
X k + 1 = x k – α g k = x k – α (A x k + d) => x k + 1 = [I – α A] xk – α d.
It is important to note that the eigenvalue of the matrix [I – α A] is used to determine the stability. The following equation satisfies the stability requirement:
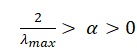
, in which λi is the eigenvalue of A
In terms of minimizing along a line, αk is chosen to minimize F (xk + αk pk). Plotting a graph creates successive steps of orthogonal.
Conjugate vectors are determined using the expression: F (x) = ½ xT A x + dT x + c. The vectors are mutually conjugate based on the positive definite matrix A of Hessian if
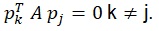
The quadratic functions are given by the following expressions:
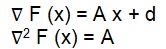
The change in the gradient at iteration k is defined using the following equation:
Δ g k = g k + 1 – g k = (A xk + 1 + d) – (A x k + d) = A Δ x k where Δ x k = (x k + 1 – x k) = α k p k.
Conjugate directions are determined by choosing the initial search as the negative of the gradient expressed as follows:
P 0 = – g 0
The subsequent search for direction is chosen using the following general equation:
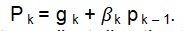
The conjugate gradient direction takes several steps. First, a search direction with negative gradient is taken. Second, a learning rate minimized along the line is chosen. The expression P k = g k + βk p k – 1 is used to determine the next search direction. A non-convergent algorithm returns the process to the second step. The resultant quadratic function is minimized in n steps.
Multilayer Perceptrons
The Newton or gradient descent methods can be used to find a minimum function using the following equation:
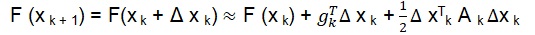
The averaging of the error energy ε av over the training set N, as a function of the weights w selected for the network, which is given as the following expression:
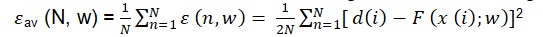
The following Taylor expansion can be applied as follows:
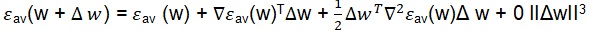
Where Ι i=1N is the training set, while F(x (i); w) is the approximating function, which is achieved by the network. The following expression defines the Levenberg-Marquardt optimization as applied to the vector w:
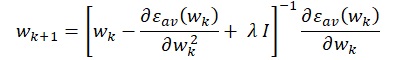
Where I = identity matrix with dimensions similar to Hessian matrix
λ= loading parameter to perform inverse operations on the positive definite matrix
In this case, small λ ~ Newton, and large λ ~ Gradient descent
Kernel Method and Radial-Basis Function Network
The chapter illustrates the Cover’s Theorem on the Separability of Patterns, which assume the existence of a set of N pattern vectors expressed as x . Each of the x represents a vector in the dimensional space m0. A set of real valued functions is defined as a column vector Φ(x) using the following expression: Φ(x)=[Φ1(x),Φ2(x),…,Φm1(x)]T. The vector Φ(x) is then mapped to points in the m0 to create a new dimensional space denoted by m0.
Support Vector Machines
The chapter illustrated the Optimal Hyperplane for Linearly Separable Patterns. With the training sample, it is possible to create a hyperplane using the support vector machine as the surface for decision in such a manner that the separation margin between positive and negative attain maximum values. A decision surface for linearly separable data based on a hyperplane takes the form of w T x + b = 0, in which x = input vector, w = adjustable weight vector, and b = bias. Langrage Theorem and quadratic optimization is also used to create a hyperplane.
Principle Component Analysis
The determination here is to describe the way in which the implementation of principal-components analysis is achieved by applying unsupervised learning. In this context, the unsupervised learning is used as the requirement for discovering significant patterns and features of the input data. This is achieved through the utilization of unlabeled mathematical models and expressions.
Self-Organization Maps
In terms of self-organization, the brain is organized in several places, and topology separates different sensory inputs that can be understood through the computational maps.