According to Anil, Karthik and Abhishek (2008), cryptographic a key must possess certain properties for it to be regarded as secure. The property, which makes the key secure include weak backward secrecy, which is based on the requirement that once a key has been used, no other member in a group is able to discover the key. Another property is the forward key secrecy. Forward key secrecy is based on the requirement that the key should be computationally infeasible. The other property is key independence, which is a requirement for ensuring that an attacker does not know the secrecy of the keys being used and cannot manage to discover the keys (Daemen & Rijmen, 2002).
Two factor key property
The two factor and the three factor schemes guarantee security on the premise that the keys are generated by combining the properties of a token, which include the smartcard and the user’s password with the biometric (OSIRIS) code. Gaddam and Lal, (2010) provide an example, which is based on a two factor scheme without a password. The security of the system, which relies on the two factor keys shows that the security of the scheme relies on the token (for storing the error correction data) and a biometric factor. An intruder cannot acquire both the token and the biometric information at the same time, which makes it difficult for the attacker to successfully intrude and compromise a system. On the other hand, if the attacker comes across the token, he will be required to have all the knowledge about the data, which is stored in the token to be able to successfully compromise the system. Because it is the first step, it is a critical step in the scheme because it is used to ensure that the attacker cannot gain access to the key once the system is compromised. Once the two factor scheme has been implemented securely, the next step is to ensure that the security level of the system is escalated by using a password (Gaddam & Lal, 2010). The password takes the two factor scheme to another level, which is known as the three factor scheme security mechanism. The three factor scheme is able to overcome attacks, which are perpetrated by sophisticated attackers.
The sophisticated attacker has the ability to extract detailed information, which is stored in a token to successfully compromise the system. Thillaikkarasi & Duraiswamy, 2010). Here, the security of the system is guaranteed on the ground that the intruder cannot access all the factors at the same time. It makes it difficult to access information on the three factors, which makes the system secure. To successfully comprise the system, one must access information about the keys. However, the shortcomings of biometric data include biometric noise, which is based on the nature of biometric data and the inability to revoke biometric data. It has been established that biometric data cannot be replaced once it has been compromised and the situation becomes worse because new templates cannot be issued, which make the biometric data to suffer the weakness of template diversity (Jagadeesan, Thillaikkarasi & Duraiswamy, 2010). However, different theories have been proposed on the methods, which can be used to extract the key from the noisy biometric data. One approach is to use the fuzzy extractor. Here an error correction code is used when an input is being supplied to the system, which is followed by the application of a hash function. The rationale for using this method is based on the argument that information, which is leaked into the hash function, does not change the entire process. However, it is important to ensure that the noise biometric data is kept secret and secure from an intruder (Gaddam & Lal, 2010).
Another approach is to ensure that different keys are used for different applications is the use of fixed permutations, which are applied to the bits of the iris-code, which are generated by use of the hashing mechanism (Gaddam & Lal, 2010).
Key Diversity
The next property is key diversity. Key diversity provides that the scheme should operate on elevated security. However, little research has been done in this area. It is not possible for another person to change the biometric properties of a person (Jagadeesan, Thillaikkarasi & Duraiswamy, 2010). In addition, it is difficult for an attacker to feign that they are the actual biometric owners because it is impossible to do so. Biometric features have been shown to be inherent in an individual and are not transferable (Gaddam & Lal, 2010). That makes it critical and important to design a scheme, which provides the user with the ability to generate different keys, which can be used in different applications such as opening a bank account. It is important to ensure that the scheme enables for the provision of keys, which can be revoked when required to do so (Jagadeesan, Thillaikkarasi & Duraiswamy, 2010).
Research studies show that biometric data cannot be kept secret and it is possible to use a camera to capture the iris image in secret using a hidden camera. It is possible to expose biometric data because of the frequency of use of the biometric template. When biometric data is used frequently, it becomes less secret. The vulnerability of biometric data makes it unsuitable for use to ensure security, when used alone. Social acceptance “makes it difficult to use biometric as a technological breakthrough” (Rathgeb & Uhl, 2011). It is possible for “biometric data to be subjected to potential abuse and misuse, leading to public distrust of the biometric keys” (Rathgeb & Uhl, 2011).
Secure key management
The security of the key depends on secure key management is a critical property of the cryptographic system which uses biometric factors such as the eye to generate the keys. In addition, the system can be used to manage the keys to make the system secure by inspiring confidence in the users of the key because the system will be assumed to prevent the threat of unauthorized access (Rathgeb & Uhl, 2011). Other issues of critical importance are key storage and recovery mechanisms to ensure that the key is securely managed. It is important to ensure that a key can be easily revoked to ensure that no users can by accident or illegally access the keys, because it has been revoked. It is important to ensure that keys are chosen randomly from the available key space. Researchers have shown that keys with a long lifespan have to be used sparingly to avoid attackers accessing and attacking then.
Withstanding reverse engineering
It should not be possible to reverse engineer the key if one is given knowledge of the algorithm and the key. Typically, it should be computationally difficult if not impossible for the other one who has the knowledge of the key to reverse engineer it (Daemen, & Rijmen, 2002).
Iris Based Key generation mechanism
Capturing details
Different iris key generation mechanisms have been developed to create a secure and reliable key. One of the methods uses the iris in a process, which consists of extracting the image of the iris (Gaddam & Lal, 2010). The captured image is then converted to binary form in a process, which involves converting the elements of the image, which exist in pixel form of the image into binary form (Anil, Karthik & Abhishek, 2008). Thereafter, the binary data is processed in a procedure known as segmentation and normalisation. The process creates edge maps after the conversion of the images into binary form. After the normalisation process is over, the cryptographic key is generated. The extraction is necessary because it provides the best method of user authentication (Gaddam & Lal, 2010). Typically, the iris has a unique pupil, which looks black in the eye and consists of other unique features including the corona and the freckles. The feature extraction process is discussed below.
Here, the iris features are extracted using a high resolution camera to capture the details of the image colors. The “camera that is used has a resolution of 2 million pixels and a frame rate of 30 fps” (Gaddam & Lal, 2010). Based on the principle of the image density principle, the image has to have a width of 1 cm, which provides a resolution of 100 microns and a cowl of 20 cm by 10 cm (Gaddam & Lal, 2010).
Segmentation
Segmentation is a critical element in the extraction of the details of the iris and provides the basis for capturing and dividing an image into segments. Segmentation is a process which is defined into two steps, which include the process of estimating the boundaries of the iris and the noise removal process (Gaddam & Lal, 2010). The “boundary estimation consists of canny edge detection, which is done in the horizontal and vertical direction of the iris image” (Rathgeb & Uhl, 2011). Here, the “exact image can be established by the use of edge detection maps and based on the Hough transformation” (Rathgeb & Uhl, 2011). Linear filtering is used to determine the gradient of the image intensity. The process involves the use of thinning and thresholds to achieve the desired binary characteristics of the image (Gaddam & Lal, 2010). A good quality image is made by removing noise in it (Gaddam & Lal, 2010). The canny operator has the ability to provide the required characteristics with a binary form of the image. It has been established that the canny operator is reliable and secure compared with other operators available today. A critical look at the Hough transformation method shows that it plays a critical role in the determination and estimation of the lines of the iris, which is critical in ensuring that the image is accurate. In context of the segmentation process, the Hough transformation mechanism provides the basis for ensuring that the each parameter of the center coordinates of the x and y axis of a circle of radius r can be calculated using the following equation:
X2+y2=r2
It is critical in the process to be able to isolate the eyelashes and the eyelids, which occlude the regions, composed of the lower and upper region of the iris. Lines are fitted to ensure that the eye lids are isolated by use of a thresholding method (Gaddam & Lal, 2010).
Normalisation
According to Gaddam and Lal (2010) the pixel intensity is adjusted to ensure that the image of the iris fits into polar coordinates of rectangle with the same characteristics as those of the iris image. The procedure is defined by two processes, which include the Angular resolution, which is based on the radial lines that are generated in the iris area and the Radial resolution, which consists of a number of data points, which form a radial projection around the iris (Gaddam & Lal, 2010). In addition, the next step is to ensure that the features extracted from the iris are encoded appropriately to generate a code of 1024 bits long using the RGB (normalized color channels). It is possible to use the 3RGB to generate 3072 bits to ensure that the image details are protected and secured against the code being generated (Gaddam & Lal, 2010).
The bits generated above can be used to generate the required 128 bit key or the 256 bit key. Here, the AES (Advanced Encryption Standard) is used to generate the private key, which can be used for encryption and decryption (Salomaa, 1996).
Key generation
It is possible to use 128, 192, and 256 bits long keys using AES. Assume that 128 bits were generated from the above conversion and the encryption is done using the AES algorithm, which is based on the encryption, which uses10 runs or rounds of the 128 bits. Each round “consists of a single byte of substitution step, followed by permutations for each row, mixing of the columns” (Rathgeb & Uhl, 2011).the next round is to “gradually add the round key to the results’ (Rathgeb & Uhl, 2011). Each action of processing the input state array generates an output state array, which consist of a 128 bit output block. Here, the “encryption key consists of 44 4-byte words” (Rathgeb & Uhl, 2011). The encryption steps include substituting the bytes, shifting the rows, mixing the columns, and adding the round keys, which then undergoes the XORing step of the output (Gaddam & Lal, 2010).
The decryption consists of “inversely shifting the rows, substituting the bytes in the inverse, adding the round keys, and mixing the columns in the inverse direction” (Gaddam & Lal, 2010). Here, the third round must undergo the XORing operation. Typically, each round must consists of four rounds, which are not discussed here.
A state array is “created at the first step with each word, which consists of a word or 32 bits, or four bytes define the columns and rows in the state matrix” (Gaddam & Lal, 2010).
Evaluation of the security of the iris key generation method
Because the generation of the key depends on biometric factors such as the image of the iris of the user, it is difficult for the attacker to compromise the system which uses the biometric system. Typically, the generation of the key depends on natural factors, which cannot be duplicated by someone else and provides the best method of ensuring the generation of secure keys (Gaddam & Lal, 2010).
Public and private keys for individuals with iris image
Yes it is possible to create a public/private key pair for individuals using the individuals’ iris images. The following discussion shows the rationale of creating and using asymmetric key cryptography instead of the symmetric key cryptography.
The private key generation is based on the symmetric key generation algorithm. On the other hand, the asymmetric key, which is also known as the public key is based on the asymmetric algorithm. Both types of keys operate differently, with the private key being used for encryption and decryption operations. The “public key algorithms are based on two keys, which include the private and public keys” (Gaddam & Lal, 2010). Here, the private key uses the hashed value of the iris code, which is generated by following the data collection, segmentation and normalisation procedures (Gaddam & Lal, 2010). The code acts as the template for the symmetric key, which can reliably be replicated when different forms of the code are hushed. The template is interoperable and can be used on different applications, which is a source of weaknesses in the security of the key because it can be used repeatedly, making the security of the system to be vulnerable. Another problem with the symmetric key is that when it is lost or intercepted or guessed, it is easy to crack the key and decrypt any cipher text in the form of the iris code. It is advisable as a precaution to change the keys frequently, a problem which is inherent in the iris symmetric key. Another challenge is the distribution of the keys. Practical evidence shows that distributing the key, which has been generated for use, is difficult and slow because it is a complex task, which requires extreme care and security to ensure the key distribution mechanism is not compromised. It has also been established that symmetric keys are subject to brute force attack. That could enable the attacker to be aware of the right key by trying out all keys in the key space to discover the right key (Gaddam & Lal, 2010).
To overcome the disadvantages associated with the symmetric keys, the asymmetric key cryptography is used. Asymmetric key encryption is also known as the public key cryptography. The public key is always available for public access and distribution and the private key is always kept secret from the world and it is mathematically related with the public key. There are different methods which can be used to generate the public key and one of the methods is the Siyal’s method. The method can be used on digital signatures based on the DSA and RSA algorithms (Anshel, Anshel & Goldfeld, 1999).
Method for generating the key
The method of generating the public key depends on collecting the features, segmenting, normalisation, and encoding of the features to ensure the correct data with error correction code is generated for key generation as shown in the diagram below (Feng & Wah, 2002).
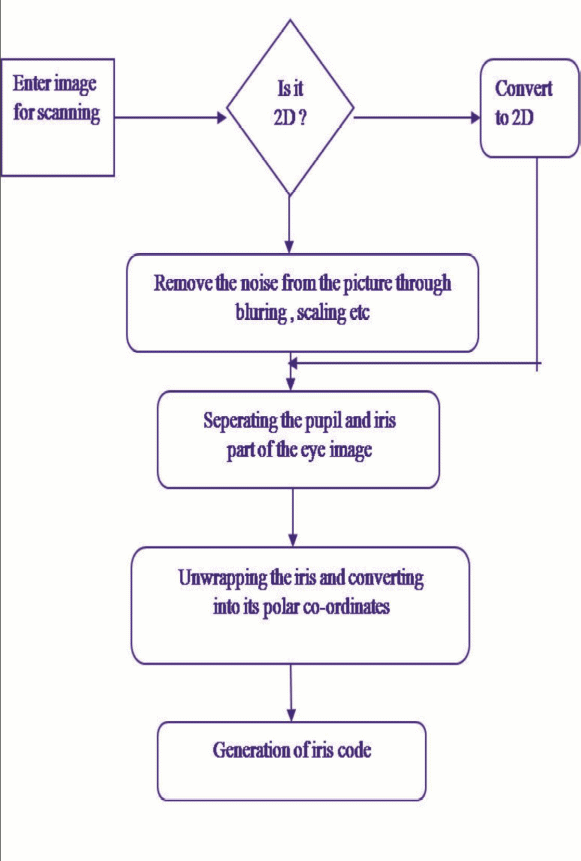
The key generation is done as follows:
Here, the numbers, which are used, are generated using the iris template. Assume that a 512 bytes have been generated using the iris template based on the Siyal method from the OSIRIS. The creation of the two keys is based on modulo arithmetic, which is not discussed here (Gaddam & Lal, 2010).
If an individual wants to perform a task (communicate) confidentially, they can use a pair of integers (e, n) as the public key and (d, n) as the private key. The public key will be used to encrypt the data and the private key can be used to decrypt the message or data being handled (Gaddam & Lal, 2010). The modulus n, which is selected, must meet the following requirement:
(Me) d = Med = M (mod n)
The encrypted message in the above expression is C=M e mod n, which underpins the need to establish the guarantee that the value of M can be decrypted by using Cd mod n. Now that the guarantee is established that the n is the product of two prime numbers (p ×q-where p and q are relatively prime numbers to each other or coprimes), then the public/private keys can be implemented as follows.
Select two relatively prime numbers p (p=13) and (q=19) for the purpose of demonstrating generation and use of the keys using the RSA algorithm.
n= p ×q = 13×19=247
n= (p-1) × (q-1) = 12 × 18 = 216.
The values of keys are KU (5, 247) and KR (173, 247).
For the iris situation, the above steps are used to arrive at the right public and private keys.
Applications of the keys
The biometric key can be applied in a wide range of areas to provide the required security, which includes password replacement and authentication purposes. It has been established that simple passwords can be easily cracked and long passwords are difficult to crack and remember. The weaknesses with the conventional methods provide evidence of the need to use biometric encryption keys, which provide better security because it is difficult to forge a biometric feature, which belongs to a specific individual (Bertoni, Breveglieri, Koren, Maistri & Piuri, 2003).
Digital signatures
Digital signature provides an additional method of securing documents to ensure that the system has additional security. In addition, if a digital signature mechanism is combined with the iris key generation mechanism, the combined security makes the approach much more secure (Bertoni, Breveglieri, Koren, Maistri & Piuri, 2003). Digital signature generation depends on the properties of the eyes, which have been discussed before (Gaddam & Lal, 2010). The following steps are critical in generating the key verify the security of the key in use.
Signature generation
When a message is hashed and some computation done on it using the MD5 or the SHAI message digest algorithm, a digital signature is generated by signing the output from the hash with m. Here, the message is encrypted using the hash mechanism and is expressed as H (m). The formula that is used is expressed as S = (H(m))d mod n where S is taken to be the digital signature and the message is encrypted by using the m+s mechanism and decrypted using the m+ S method (Bertoni, Breveglieri, Koren, Maistri & Piuri, 2003).
Two important properties
For the key generation to be effective, and to enforce the require security, the algorithm used must not allow the key to be mathematically computed if the attacker is given the knowledge of the encryption algorithm and the encryption key (Garfinkel, 1996). It is critical for each system to be able to generate its own key. When generating the keys, it is important to ensure that the large integers, which are the coprimes that are used.
References
Anil K, J., Karthik, N., & Abhishek, N. (2008). Biometric template security. EURASIP Journal on Advances in Signal Processing, 1(2), pp.34-45
Anshel, I., Anshel, M., & Goldfeld, D. (1999). An algebraic method for public-key cryptography. Mathematical Research Letters, 6 (2), 287-292.
Bertoni, G., Breveglieri, L., Koren, I., Maistri, P., & Piuri, V. (2003). Error analysis and detection procedures for a hardware implementation of the advanced encryption standard. Computers, IEEE Transactions on, 52(4), 492-505.
Daemen, J., & Rijmen, V. (2002). The design of Rijndael: AES-the advanced encryption standard. New York: Springer.
Feng, H., & Wah, C. C. (2002). Private key generation from on-line handwritten signatures. Information Management & Computer Security, 10(4), 159-164.
Gaddam, S. V., & Lal, M. (2010). Efficient Cancelable Biometric Key Generation Scheme for Cryptography. IJ Network Security, 11(2), 61-69.
Garfinkel, S. L. (1996). Public key cryptography. Computer, 29(6), 101-104.
Jagadeesan, A., Thillaikkarasi, T., & Duraiswamy, K. (2010). Cryptographic key generation from multiple biometric modalities: Fusing minutiae with iris feature. Int. J. Comput. Appl, 2(6), 16-26.
Rathgeb, C., & Uhl, A. (2011). Context-based biometric key generation for Iris. IET computer vision, 5(6), 389-397.
Salomaa, A. (1996). Public-key cryptography. Berlin: Springer.