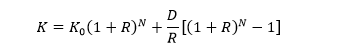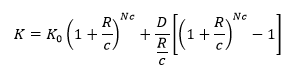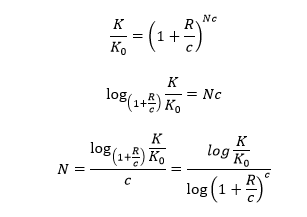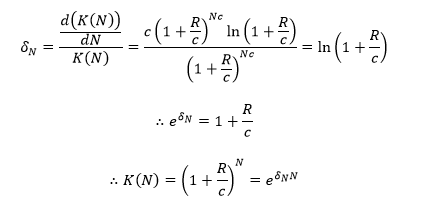Introduction
Mathematics is an exact fundamental science that allows us to explore the world through a numerical-character alphabet through the study of orders and patterns. It is one of the oldest sciences since, even in primitive communities, the distribution, counting, and division of resources were critical tasks. By now, however, mathematics has become much more complex, extensive, and diverse than it was thousands of years ago, but its overall core, the study of the relationships between objects, has remained unchanged. It is noteworthy that mathematics is not didactically related to the natural sciences, but their existence without the use of mathematical apparatus turns out to be impossible.
In other words, many fields of knowledge use mathematical formulas, theorems, and axioms as tools-not surprising at all, given how diverse this science is. Anything from analytic and applied geometry, calculus, differential equations and functional analysis, linear algebra, and even number theories is the subject of mathematics. In this extended essay, in an attempt to narrow the range of mathematical studies to a single topic for the purpose of more in-depth study, the direction of interest calculus, mainly compound interest, has been chosen. A fundamental thesis reflected throughout the paper is that compound interest is a more complex and ambiguous problem than students are used to perceiving it.
This extended essay sheds light on the use of interest — in priority of compound interest — to solve many applied problems. The widespread view that compound interest can be helpful only in financial calculations is critically evaluated in the paper: counterarguments are offered to the reader. The essay, however, aims at a deeper study of the compound interest model in the economic sector as well, since it will be shown that the use of mathematical operators, whether limits or differentiation, over the compound interest formula is of applied importance. The didactic benefits of this essay include a broad but critical discussion of the history of compound interest through a literature review of academic and Web sources. It will be shown that compound interest was first used much earlier than is commonly considered. Ultimately, the entire extended essay is a critical assessment of the topic of compound interest and the prospects for its application to life’s problems.
Background Information on Percentages
In mathematics, the use of a fraction of any number is called a percentage. In everyday life, the individual tends to interact with percentages all the time if it is necessary to count the number of discounts, the amount of a loan payment, or premium deductions to a paycheck. The concept of “percent” in general is one of the essential tools of mathematics since it allows us to quantitatively perceive fractions of the whole in order to compare them later. In general, a percent is commonly referred to as one-hundredth of a part in relation to the whole, denoted by the special symbol “%.” For example, one of the tasks of percentage mathematics may be to use the following calculation scheme shown in the equation [1].
In the above example, one can clearly see that percentages refer to the part — or fraction — that a component takes from the whole system: in this case, the head from the mass of whole body. In other words, the methodological notation of percent can be represented as shown in equation [2], where A and B are part and whole, respectively. In this sense, it is essential to note that mathematics allows us to modify this formula as one wishes — while preserving the logic of calculations — which means that one can solve the inverse problem. Hence, knowing what percentage of a component takes from the whole, it can always be found the numerical characteristic of that component, be it mass, finance, distance, or any other characteristic used in a particular problem.
It is true that the term interest has become synonymous with the word interest, having a direct bearing on banking. This is not surprising since one of banking’s key objectives is to increase its profits through various investment instruments, be they deposits, start-ups, stocks, or bonds. In this sense, interest refers not so much to the fraction of the part of the whole but to the portion added to the sum of money. For example, when an individual puts a deposit in a bank with interest, it means that they expect to increase the size of their deposit in the bank by the amount of the interest portion that changes the structure of the deposit monthly, quarterly, or annually (Fernando, 2021). To put it another way, there is an opaque relationship between the terms “percent” and “interest,” but the focus of this extended essay is precisely on the nature of compound interest, dealing with added value.
Accruing interest on a sum of money, repeated periodically, allows a qualitative increase in the initial investment size. This can be done either with simple interest or compound interest, with the second method winning significantly even in the short term. It is important to emphasize that it is the financial calculus that is used here as one of the most obvious, although it will be shown later that the interest surcharge model is not only applicable to finance. The simple interest accrual is understood as a formula for a linear relationship between the final amount and the number of years as an independent variable. Equation [3] shows that the final deposit amount, K, always depends on time N. Additionally, [3] also includes variables of initial deposit amount K0 and interest rate R offered by banks: but as these values do not change with time, they can be neglected in simplification of the formula.
Thus, if the constants are assigned random numbers — for instance, K0 = 100 and R = 0.05 — then the resulting function will have the form shown in Figure 1. This confirms the linear relationship between the variables of interest, but it does not create the most favorable conditions for the investor. For example, if an individual initially invests only $100 at five percent per annum, then after ten years, their winnings will be only $50, which obviously cannot be a financially wise decision.
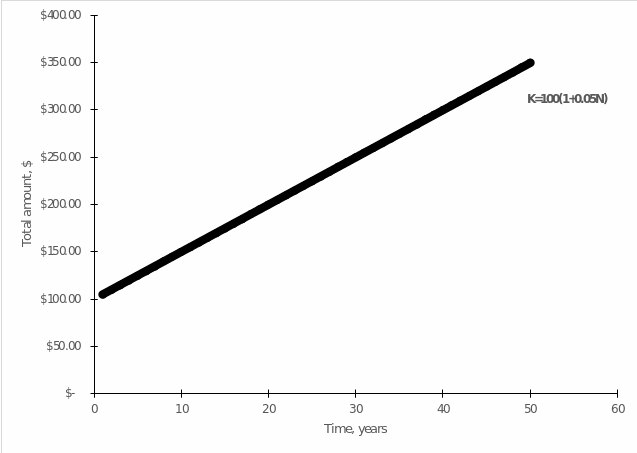
The way of investing through which the investor can win is called compound interest. In contrast to the simple interest model, in this case, there is a systematic capitalization of profits, which allows the individual to qualitatively increase their income no longer by linear dependence but by exponential dependence. Equation [4] shows the formula for compound interest: In this formula, one can see that the variable of the final sum is no longer in direct linear dependence on time N, but instead, N finds itself in power. In particular, if one leaves K0 and R the same as was relevant for simple interest, one can see that ten years after the annual capitalization, the amount deposited will already be $162.89, nearly nine percent higher than with the simple interest model.
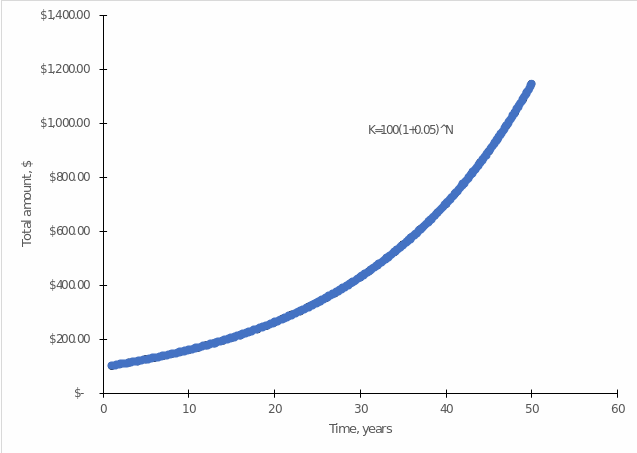
To put it another way, compound interest works as added value on a constantly changing amount. In this case, each year, the amount is replenished by the stated rate: this is clearly visible in the two figures and the table below: in the first year of investment, the amount deposited for both types of interest accrual was equal. However, in the case of compound interest from the second year onward, the interest charge is no longer imposed on the initial deposit amount, that is, $100, but on the new amount, that is, $105. This snowball mechanism allows the total amount to constantly increase so that, under the conditions in question, an individual would receive 328 percent more in fifty years than on simple interest.
Calculations of Different Interest Accrual Schemes.
It is clear that the cumulative effect is strongest with long-term accumulation, although compound interest deposits have an excellent increase even in the early years, as shown in the table above. Moreover, it is essential to note that compound interest is rarely used by investors only for zero deposits; instead, additional systematic capitalization, such as regular payroll deductions, is an essential practice to enhance the exponential effect (Fernando, 2021; Hazell, 2021). In this case, it is evident that the compound interest formula is modified and becomes as shown in Equation [5].
 | [5] |
It is interesting to trace how the transformation [4] into [5] will affect the shape of the graph and how these changes have a benefit for the investor compared to simple interest. Figure 3 allows us to do this: several conclusions can be formulated at once from the data of this visualization. First, it is clearly seen that compound interest investments with annual additions have a severe advantage for future profits because there is a qualitative increase in profits. In this case, it is essential to say that after fifty years of investing, the total amount from the initial deposit of $100 and 20 annual additions was $5,333.70, with a total investment of $1,100: so the total return over fifty years was $4,233.70 for this investment scheme or 384.99 percent.
For compound interest with no additional investment, the return after fifty years was $1,146.74, which, given the $100 initial investment, was $1,046.74 percent. In other words, compound interest with no investment gave the investor a more significant return in interest but a smaller return in equity. Third, investing at simple interest had absolutely no advantage for the investor because it lagged far behind in both the interest benefit and the amount of capital received. From this, it can be drawn only one key conclusion — compound interest is a priority.
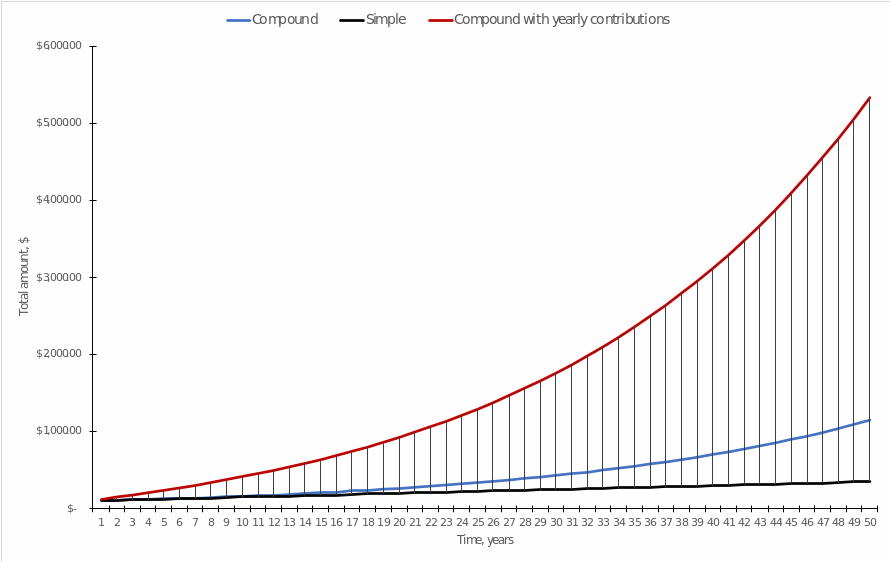
A few additional important points in terms of basic and functional mathematics must be said about the compound interest formula and Figure 3. It can be seen, visually that the growth rate of the compound interest function with an additional deposit is higher than for compound interest without an annual investment. Second, from an economic point of view, it matters precisely when the current deposit is made, at the beginning or the end of the reporting period. For comparison, if the deposit is replenished annually at the end of the year, it will ultimately earn the investor $5,333.70, but if the replenishment occurs at the beginning of the year, the total increases to $5,543.05, as shown in equations [6] and [7].
 | [6] |
| K_beggining=5543.05 | [7] |
Finally, what has not been saying before, but which makes important sense for studying the subject of compound interest, is the number of additions during the year. Up to now, all of the formulas used have assumed that the action on the deposit takes place once a year, either at the beginning or the end of the year. In practice, however, replenishments do not necessarily occur only once: instead, a deposit can be replenished every month, quarter, or half-year. To mark this, the formula [5] must be corrected by adding a variable 
showing the number of actions from deposits during one year, as shown in equation [8]. In the case of a one-time replenishment per year, 
was equal to one, but if deposit actions occur, for example, every six months, then c=2 should be factored into the formula. If, on the other hand, there are monthly replenishments, in which case c=12.
 | [8] |
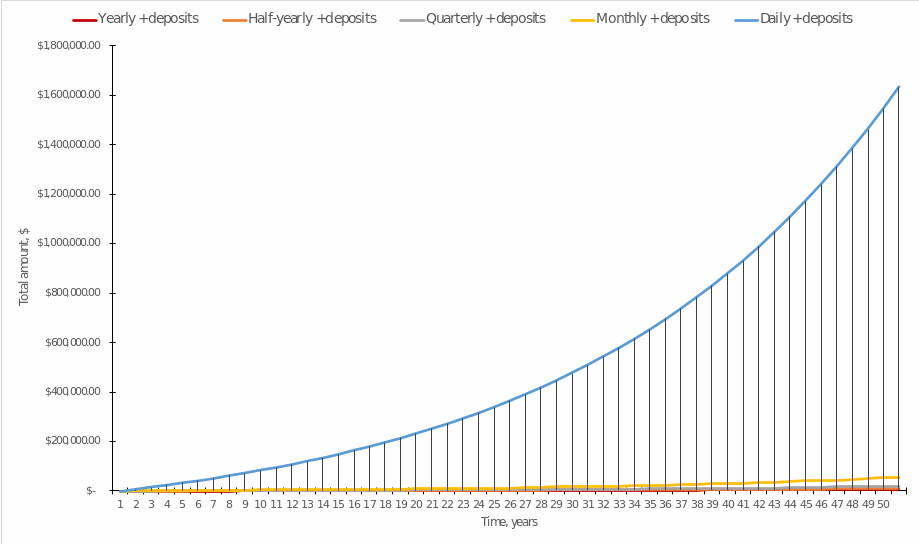
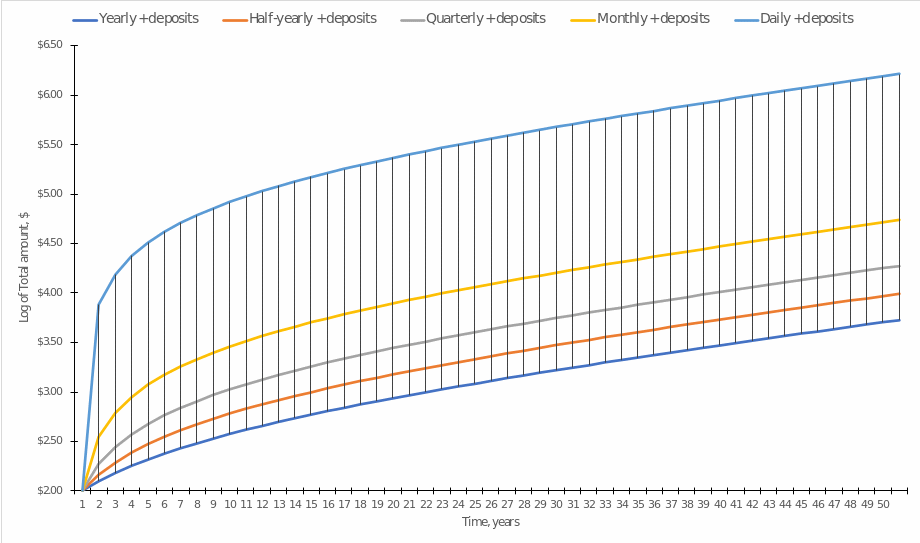
In this context, it is intriguing to clarify which way of calculating compound interest — annual, every six months, every quarter, or every month — under the appropriate replenishment scheme will ultimately have an increased benefit for the investor. If one leaves all the other variables as they were before, but manipulate variable 
, then the data from Figure 4 can be obtained. It can be seen that the daily computation of compound interest is a more attractive scheme in terms of economic growth, but an apt comparison of the data proves to be complicated by too different scales. Then one can use the logarithm of the vertical axis to compare the data, which yields Figure 5 (Bex, 2020).
It can be seen that the growth of the deposit total directly depends on the mode of calculation of the compound interest: the more minor arithmetic operations took place during the year, the smaller the total amount was accumulated at each point in time, except in the zero year. This is fully supported by investment practice, but it is entirely disadvantageous for banks, which will lose more of their money by charging interest more often. Hence, the more often the interest addition is done on the increasing amount, the more money the investor will eventually get.
The last point to be said in this section is to make the formula for compound interest without additional investment universal so that it can be used later. Equation [4] already showed a compound interest that dealt with a one-time accrual of interest from the bank during the year. But as one already knows, this formula must be corrected in [9] to become universal.
Some Mathematical Properties of the Compound Interest
The exponential form of the compound interest function makes it possible to explore this model in more depth using the advanced tools of the mathematical apparatus. One of the most apparent actions is to express the time N, finding which is a frequent practical problem in investment mathematics. Equation [10] shows an inversion of the equation [9]. For example, if one wants to determine the time it takes for an initial investment of $100 at an interest rate of 0.05 to triple in monthly compound interest, using the formula [10], one can see that the approximate answer would be 22.5 months or almost two years.
 | [10] |
At the same time, it is possible to calculate the total net profit to be obtained from the deposit over time. To do this, the variable I is introduced, which is numerically equal to the amount remaining after subtracting the initial investment from the income received: equation [11]. In this case, it becomes possible to express the amount of initial capital that must be invested in order to achieve a specific return, as shown in equation [12].
Simultaneously, it is interesting to consider a continuous function in which 
will tend to infinity. Under these conditions, it has already been estimated that the more often the compound interest is computed, every day, the greater the benefit to the investor and the higher the growth rate of the exponential graph. In the case of 
, one can obtain the equation [13]. From the derivation of the finite equation, it can be seen that if the number of accrual periods is maximized to infinity, the final investment size function is exponentially related to the number of years through the initial return coefficient.
 | [13] |
As mentioned earlier, the accumulation function K (N) can ignore the initial investment 
to simplify the calculation. In this simplification, it becomes possible to calculate the value of the force of interest as a differentiable function. The power of interest 
has a physical meaning as the interest rate R, which has been aspirated to infinite accrual. Among others, this makes it possible to calculate the time value of money.
 | [14] |
A Brief History of Compound Interest
As is clear from the previous section, the use of compound interest is of high value to society, which is why it is expected that compound interest was developed quite a long time ago. One of the most popular versions of the origin of the compound interest is taken to be their discovery in seventeenth-century Italy as a percentage by percentage, although there are fragments indicating an even earlier use of the model. There is evidence that confirms the ancient Babylonian origin of the compound interest, which had the characteristic name şibāt şibtim among the locals (Muroi, 2015). At the same time, some evidence points to the existence of interest accrual as early as the Sumerian civilization, which dates back 2500 millennia.
In particular, remnants of ancient Sumerian clay slabs have been found on which interest conditions for borrowed grain were indicated (Friberg & Al-Rawi et al., 2016). This is interesting because neither Sumerian nor Babylonian civilizations used a mathematical apparatus in the form familiar to modern people and did not even have zero but could operate with the concepts of interest on interest and count the amount needed to repay the debt increasing exponentially with each year. The practice of using compound interest was borrowed by the inhabitants of ancient Babylon, and the discovered clay tablet VAT 8528 shows this:
Equation [15] is what was dissected on this clue tablet, and Muroi (2015) interprets this as taking compound interest under five years. Figure 6 shows a modern reading of the clay tablet, from which it is clear that the borrowed grain was taxed with compound interest every five years.
The study of the compound interest model continued in the last millennium. In the Middle Ages, compound interest was rationally described by Francesco Pegolotti in his writings Pratica Della Mercatura, where the Florentine described in detail basic trading practices, including taking a sum at interest (Brunner, 1936). Nearly half a century later, at the end of the fifteenth century, the famous Italian mathematician and founder of modern accounting, Luca Pacioli, invented the famous Rule 72, which is used to estimate the time it takes to double the return on a deposit (Buchen et al., 2017). A significant figure in the mathematics of compound interest was Richard Witt, who published a book in 1613 devoted entirely to compound interest alone (Lewin, 2019).
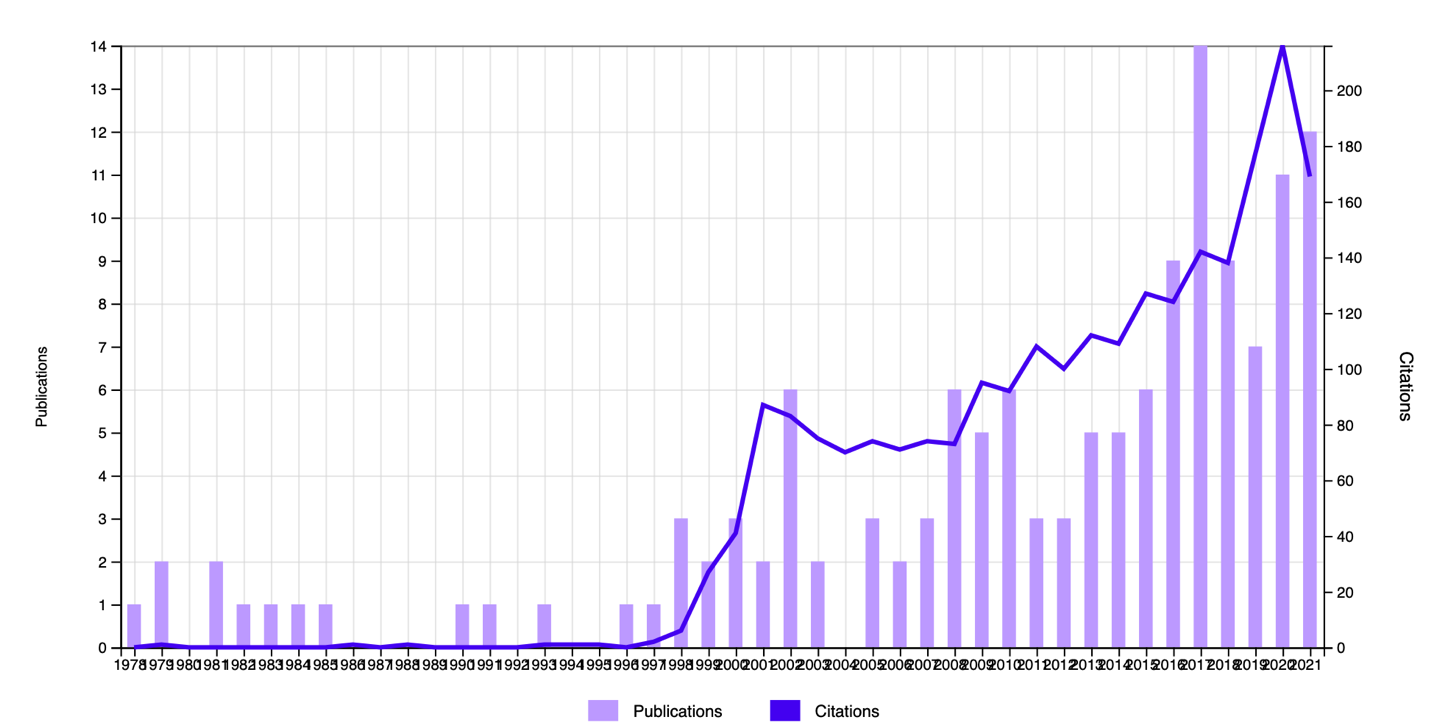
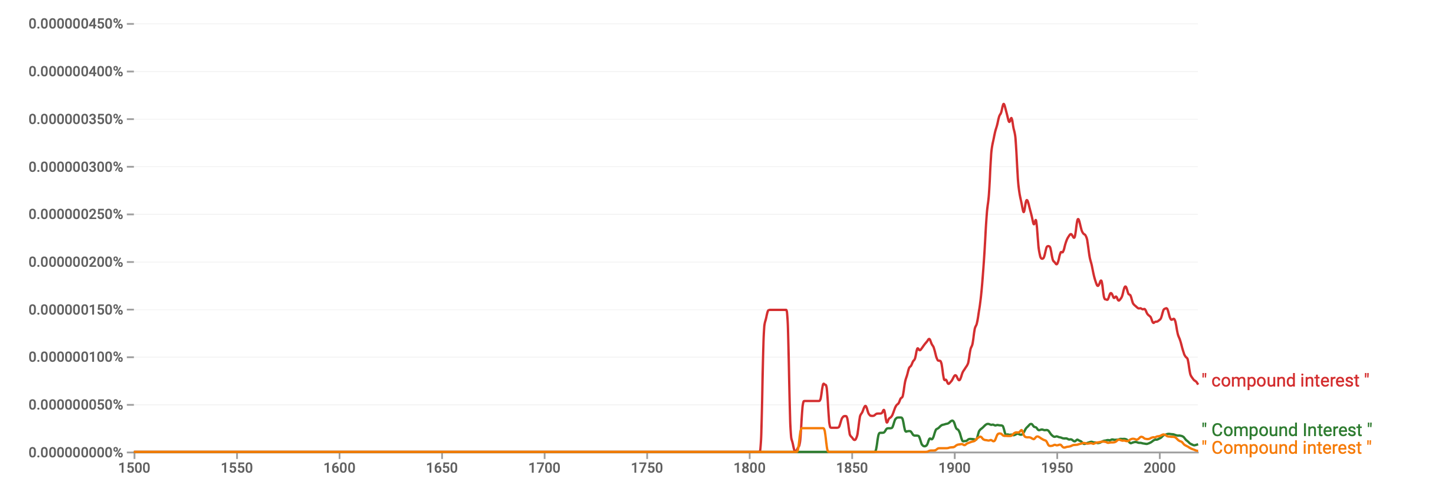
This was an essential milestone in the history of the study of this topic, since before, academics had not paid sufficient attention to this particular area of mathematics. In terms of the interest of the contemporary academic community, Figure 7 makes it clear that the topic of compound interest has only gained a particular interest in the last 20-25 years. At the same time, Figure 8 shows that there were individual peaks of interest in 1815, 1835, and 1924 for authors of printed books to mention the term. Thus, the history of compound interest has several landmark episodes and is closely related to trade and economic development.
Potential Uses of Compound Interest
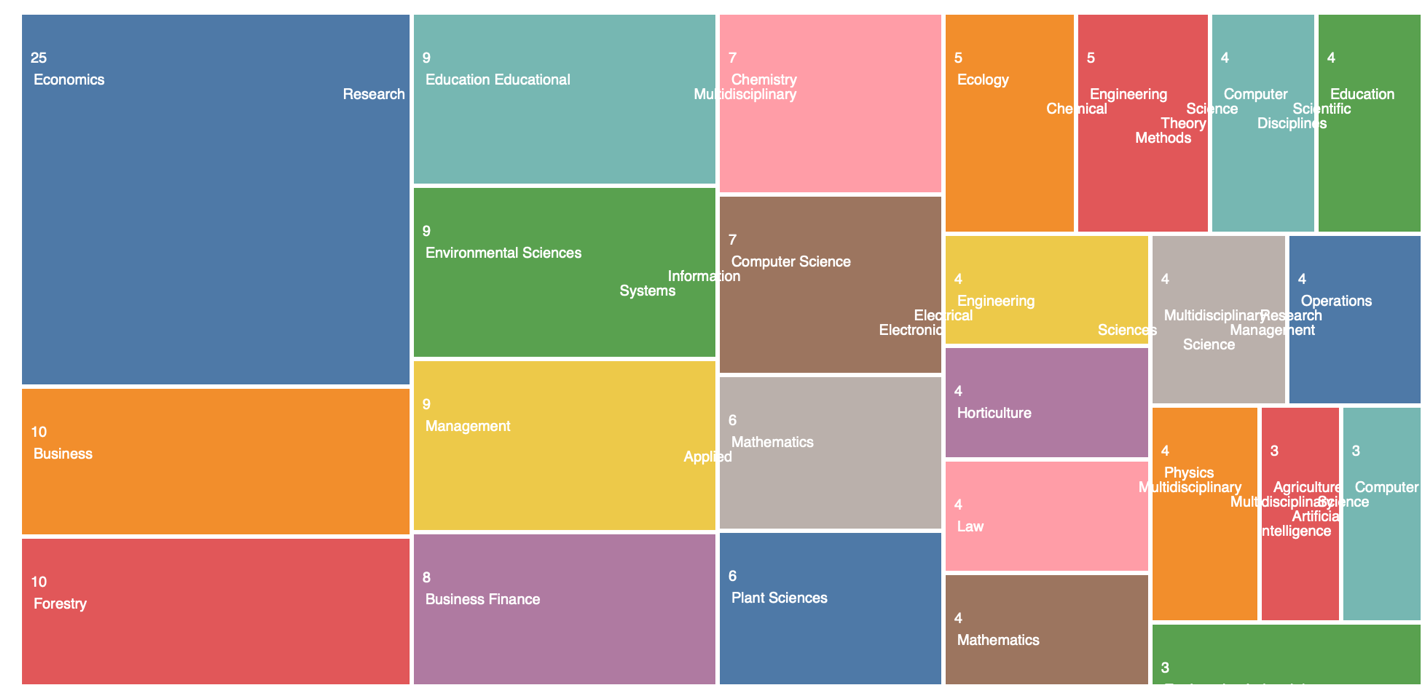
Throughout the previous sections, it has been shown that compound interest has a high value for deposit banking operations if the investor’s goal is to multiply equity capital qualitatively. The financial vector of use also includes accumulation on corporate dividends for investors, retirement growth opportunities, and capital appreciation on stocks and bonds. In reality, however, it is a mistake to limit the use of compound interest only to this area. A study of the Web of Science academic tool makes it clear that the concept of compound interest is being explored in fields of knowledge such as environmental science, chemistry, computer science, ecology, botany, and others, which are represented in Figure 9.
Konkel (2017) used the compound interest model to estimate the cumulative toxic effects of chemicals that are hazardous to humans. Liu (2020) uses compound interest at the intersection of economic and oceanographic sciences to predict port structures’ development. Sweetman et al. (2019) show with a compound interest model that forested areas are declining rapidly, a trend that will carry weight in the near future. Compound percentages have applications in medicine as well: Reeves et al. (2017) have shown that treating HIV patients with antiretroviral therapy using compound percentages, by continually increasing treatment capacity, can ultimately improve therapy outcomes meaningfully. In this sense, one of the most notable studies is the work of Han et al. (2014), who summarized that “compound interest law, which exists in many natural phenomena…” (67).
The authors of this study, in particular, used compound interest to assess the applicability of this law to the increase in seed bank size of monocotyledonous plants, based on the assumption that there is a non-obvious relationship between the idea of compound interest and evolutionary development. Thus, the overall conclusion is that compound interest can be used in many fields and is not limited to applications in the financial sciences alone, whether in deposits, bonds, or stocks.
Conclusion and Critical Perspective
To summarize, the first point to emphasize is that compound interest is just a mathematical fact that allows creating an additive on the value add. Albert Einstein once said that compound interest is one of humanity’s most ingenious inventions, and in light of the applications of the concept discussed, one cannot disagree (James, 2018). In particular, compound percentages find their application in the biological, chemical, environmental sciences, and even beyond. Compound interest allows returns to increase dramatically even in short periods of time because, unlike the simple interest model, compound interest operates with exponential growth.
It has been mathematically proven that increasing the number of acts of compound interest — for example, moving from annual to daily — significantly increases profitability. When the number of acts tends to infinity, the compound interest formula undergoes a transformation, with, as expected, profit growth being faster than for compound interest with a one-time accrual. Adding additional deposits also increases profitability: it makes sense, for example, if an individual is willing to give part of their paycheck each month to invest in compound interest. Again, the more often additional investments are made, the higher the amount of the final accumulation at the end.
Thus, the benefits of compound interest are apparent: it brings faster and sharper growth, it makes money “work for itself,” and it produces excellent results, eventually, literally increasing the profitability of the investment every day. Compound interest is an example of geometric progression, which means the growth proves to be highly effective. However, compound interest is not without its disadvantages. One of them is the need to constantly add deposits if the method of additional deposits was chosen as a reinvestment scheme. In addition, banks are reluctant to accept compound interest because, in this case, they have to give more than they receive. In addition, it is the compound interest that is often used by creditors, which provokes the bankruptcy of millions of citizens.
References
Bex, T. (2020). Logarithmic scale in data science: How to plot and actually understand it. Towards Dev. Web.
Brunner, O. (1936). Pegolotti Francesco Balducci, La pratica della mercatura, edited by Allan Evans (book review). Web.
Buchen, P., Partington, G., Philip, R., & Satchell, S. (2017). Returns and doubling times. Web.
Fernando, J. (2021). Compound interest. Investopedia. Web.
Friberg, J., & Al-Rawi, F. N. (2016). Three Old Babylonian recombination texts of mathematical problems without solution procedures, making up group 2b. New Mathematical Cuneiform Texts, 421-480.
Han, Z. Q., Liu, T., Sun, Q., Li, R., Xie, J. B., & Li, B. L. (2014). Application of compound interest laws in biology: Reunification of existing models to develop seed bank dynamics model of annual plants. Ecological Modelling, 278, 67-73.
Hazell, A. (2021). Compound interest formula with examples. The CS. Web.
James, D. (2018). Compound interest is the root of banks’ evil. Eureka Street, 28(24), 83-85.
Konkel, L. (2017). Compound interest: Assessing the effects of chemical mixtures in vivo. Environmental Health Perspectives, 125(12), 1-2.
Lewin, C. G. (2019). The emergence of compound interest. British Actuarial Journal, 24(e34), 1-27.
Liu, J. (2020). A grey theory-based economic prediction method of port and ocean engineering. Journal of Coastal Research, 106(SI), 197-200.
Muroi, K. (2015). The oldest example of compound interest in Sumer: Seventh power of four-thirds. Web.
Reeves, D. B., Duke, E. R., Hughes, S. M., Prlic, M., Hladik, F., & Schiffer, J. T. (2017). Anti-proliferative therapy for HIV cure: a compound interest approach. Scientific Reports, 7(1), 1-10.
Sweetman, B. M., Cissell, J. R., Rhine, S., & Steinberg, M. K. (2019). Land cover changes on ambergris Caye, Belize: a case study of unregulated tourism development. The Professional Geographer, 71(1), 123-134.