Introduction
Learning disorders or learning difficulties are sunshade terminologies that are used for a range of learning problems. According to Chinn Steve (2004), a learning difficulty is never an intelligence problem in the sense that children with these complications are not lazy or dumb. Most of them are just as intelligent as any of the others; the only difference is that their brains are chained differently (Aaron 2005). These distinctions influence how they receive and decode information. This ultimately means that children and grownups with learning difficulties see, hear, comprehend and decode things distinctively. The effect of this problem is that it leads to difficulties in learning new skills and information as well as implementing them (Renée, Louis &Hallahan, 2002).
The most popular types of learning difficulties encompass reasoning, reading, writing, listening, math and speaking problems. Some of the learning disabilities include dyscalculia which is all about math and geometry problems, dyslexia, Attention deficit disorder (ADD), dyspraxia, verbal-linguistic function, time management, memory, stress management and orientation in space among others (Lerner, 2000). The ultimate aim of this context is to examine a profile of a student with special need of assistance with geometry. The student has a problem of dyscalculia particularly in geometry and therefore, the report presents several diagnostic sessions with the child. It winds up with an intervention plan for the child’s problem.
Profile of a student with learning difficulty
- Name: Kenny Jones
- Gender: Male
- Date of Birth: September 18, 2005.
- Nationality: Australian
- Region: Sydney Australia
Description of his learning difficulties
Kenny Jones is a young student, currently in year two in primary school in Sydney, Australia. He is a clever boy who comprehends English, Science and History very well but has a problem with mathematics. He was doing well in the other subjects, but it seemed he did not comprehend geometry at all. He was even developing negative attitude towards the subject because he did not love his poor performance in the subject.
Nevertheless, after the teacher assessed him, he realized Jones had learning difficulty in mathematics particularly in comprehension of geometry sessions. The teacher discovered that Jones could not recognize increase and decrease in number series involving twos and fives as well as recognition of missing components in a number sequence. He could not represent multiplication through grouping items into sets. He had not understood any concept concerning multiplication because he could not do even the simplest multiplication geometry.
It was very difficult for him to illustrate calculations as well as represent the value of Australian currency using distinct arrangement of notes and coins. Kenny Jones was very poor in assessing dimensional shapes because he could not draw two-dimensional shapes. It was also difficult for him to identify and employ the concepts of three-dimensional objects to arrange and group them as well as explain how the sliding, flipping or turning of an object can alter its shape or size. This was a major problem because this part was very interesting and almost all the other students in his class had understood these concepts and were enjoying them since they involve diagrams and drawings. Children love things to do with modeling, depictions and dimensions but Jones seemed to be the odd one out.
However, the most disappointing part of it was that Jones could not illustrate addition and subtraction calculations from word problems (Chinn, 2004). Most children begin by comprehending the subtraction and addition problems in geometry, and that was the simplest problems according to the other students in his class.
This shows that indeed, Jones had learning difficulty in Mathematics and his dyscalculia was very serious. Other problems included understanding fractions, reading the time, classification of possible and impossible calculations, drawing graphs and columns and designing of simple maps (Butterworth, 2004). Therefore, the teacher decided to isolate him from the rest of the class and have private sessions with him to enable him resolve the problem of dyscalculia.
Diagnostic Sessions
The teacher was intelligent in his approach to Kenny Jones. He first talked to him and let him understand that mathematics is a subject like any other, and can be interesting when done with passion. The teacher stated, “The first thing to be done is to eliminate the ‘I cannot make it’ attitude in your mentality and then develop the passion in the subject and you will make it” (Sharma, 1999).
He then asked Jones why he thought geometry was difficult to comprehend and why he had the negative attitude towards the subject. Jones denoted that every time he did an assignment, he always failed and that it was difficult for him to understand anything in mathematics because he believed geometry was difficult. Eventually, the teacher convinced him that geometry was interesting when followed keenly. Therefore, he began his sessions with him by taking him through the addition and subtraction process.
First, he taught him how to count to and from 1000 and to perform simple mathematics using sticks. For example, he showed him how to calculate one plus one by putting one stick and adding another one to it (Attwood, 2002). Through those simple counting and calculations, Jones was able to comprehend the entire process of addition and subtraction. The following day he took him through multiplication and division process. The teacher used the system of grouping objects into sets as well as using drawing to explain multiplication process.
For example, he used the method of grouping to help Jones understand that if a person had 5 chairs each with 4 cats, the total number of cats he has are 20. This is implicated in the following diagram. Jones seemed to enjoy the process, as he was noted, “this is interesting, I think it is very simple” (Chinn, 2004). Eventually, Jones comprehended the entire process of multiplication and was glad to inform his teacher that he can multiply. He also loved the process of modeling using a variety of materials and solved problems using models. To make sure that Jones grasped and comprehended every aspect of it, the teacher took him back to class where he interacted with his colleagues (Butterworth, 2004). They were able to pose their multiplication problems for others to solve and discussed the steps they used to work out their multiplication problem.
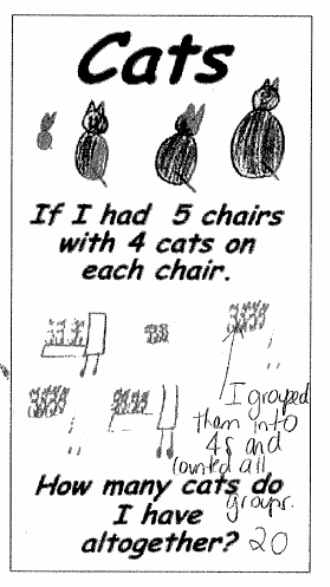
The teacher employed the same process of teaching Jones for every private tuition they had (Sharma, 1999). He was able to accomplish topics such as units of measurement (patterns are related to time), fractions (halves, quarters and eighths), money (show me money), shapes (two-dimensional shapes and three-dimensional items), transformation (flip, slide and turn), location (bike track), place (sequencing) and numbers (I can multiply) (Renée, Louis & Hallahan, 2002). The same method needs to be adopted by other teachers and parents to solve the problem of learning difficulties in geometry among their students and children respectively. It is clear that, after his second year in school, Kenny Jones will be out of this problem and he will be in a position to perform even better (Attwood, 2002).
Identification and description of learning difficulty
For an individual diagnosed with learning difficulties like Jones, the situation always appears to be creepy at first. Nevertheless, a learning difficulty is not connected to the intelligence of an individual – after all, victorious people like Alexander Graham Bell, Walt Disney, and Winston Churchill had learning difficulties (Reid & Weatherly, 2004). Therefore, despite what Jones is going through, he will still be successful in life if only his parents motivate, inspire him and support him as well as his mathematics teacher for his wonderful work.
Note that learning difficulties are problems that influence the ability of the brain to acquire process, evaluate and keep information. These difficulties can cause a student to learn as faster as someone who is not influenced by learning disabilities, exactly what happens to Jones as far as other subjects like English, science, and history are concerned, but it may as well be the opposite Jones’ geometry difficulty.
Dudley-Marling (2004), puts it clearly in her book “The Social Construction of Learning Disabilities,” that several students affected by learning disabilities have more than one type. This is different in Jones’s case although he only has geometry difficulty but in several sub-topics.
Just as observed on Jones, most learning difficulties interrupt a person’s ability to focus and be attentive and may make an individual’s mind meander too much. Jones was even giving up in mathematics since he had already developed a negative attitude towards it (Dudley-Marling, 2004). The system through which the human brain processes information is intensively complicated.
For instance, when a person looks at an image, the brain of such individual not only creates lines into the picture but also has to identify what the picture stands for; associate that picture to other facts kept in the person’s memory, and then keeps this new information (Reid & Weatherly, 2004). The same thing happens with speech; people have to identify the words, understand their meaning and fathom the essence of the statement to people. Several of these actions occur in distinct parts of the brain, and it depends on the individual’s mind to connect them together.
Nevertheless, Kenny Jones should be aware that he is not alone because several students are diagnosed with learning disabilities. In fact, almost four million school-age children and teens have learning difficulties. About 20 percent of the children have certain kinds of disorders that make it hard for them to concentrate. Generally, Jones is catching up and he will soon be out of the problem especially if he considers the following recommendations.
Recommendations for Jones’ Future Learning
As a child grows older, so does education become complex. Since Jones is developing and he will soon move to junior primary and later to senior, the learning difficulty in geometry as well as others like dyslexia, ADD, and many others may develop. Therefore, the following processes should be implemented especially as far as geometry difficulty is concerned.
Developing the precise neural configuration needed for learning progression
The precise brain configuration needed for the learning progression generates in sequence during the early life of a human being. According to Howard Gardener, the MD of Harvard University, seven foundational forms of intelligence arise during distinct phases. These are body-kinesthetic-motoric abilities, musical rhythmic abilities, visual-spatial abilities, verbal-linguistic abilities, logical-mathematical skills, interpersonal abilities, and intrapersonal abilities (self-awareness). According to Gardener, when the neurological nuance that develops from the growth of these abilities is not sufficiently established, the bio-neurological nuance is barged in, leading to an ailment in cognitive and overall operation (Renée, Louis &Hallahan, 2002). Therefore, specific neural configurations must be developed using brain plasticity, which compensates neurological configurations.
Teaching the brain to manage two-dimensional acuity and insight
Establishment and maintenance of two-dimensional insight (the skills to change shape into a symbol and to decode letters and words) are significant for the growth of influential learning skills. Appropriately, developed two-dimensional insight permits the appropriate establishment needed to recognize and observe directions and continuity. Course and permanence are both needed for the reading process, which involves sensitivity to letters, words, sentences, and paragraphs in context, as well as interpreting comprehension, generating issues and linking ideas. Two-dimensional sensitivity is significant for creating arithmetic abilities. This discernment is attained by developing permanence that is taught through enumerating or counting, therefore, achieving quantitative perception and simplifying skills.
Teaching the brain in phonological skills
This teaching is the development of phonological consciousness, which gives the customer the skills to access and translate phonological information linked to the written message – this means decoding of information from sound to symbol.
Learning and Memory strategies
This encompasses memory system, comprehension and abridging, revision techniques, association mapping, essay writing, stress control, and time management.
Note that all these processes are focused and effective neuro-cognitive minimization techniques that help to eliminate learning disorders. Attwood Tony (2002), a state in their book, “Dyscalculia in Schools,” that effective neuro-cognitive method motivates the brain to create precise brain configurations that are significant for the learning progression; they can also create practice strategies for managing brain actions and teach the brain to attain well-developed two-dimensional insight.
References
Aaron, P.G. (2005). “Differential Diagnosis of Reading Disabilities”. School Psychology Review 24 (3): 345–60.
Attwood, T. (2002). Dyscalculia in Schools: What It Is and What You Can Do. School Psychology Review 24 (3): 44.
Butterworth, B. (2004). Dyscalculia Guidance: Helping Pupils With Specific Learning Difficulties in Maths. London: David Fulton Publications.
Chinn, S. ( 2004). The Trouble with Maths: A Practical Guide to Helping Learners with Numeracy Difficulties. London: Routledge.
Dudley-Marling, C. (2004). “The Social Construction of Learning Disabilities.” Journal of Learning Disabilities 37(6):482-489.
Lerner, J. W. (2000). Learning disabilities: theories, diagnosis, and teaching strategies. Boston: Houghton Mifflin.
Reid, D. & Weatherly, V. (2004). “The Discursive Practice of Learning Disability: Implications for Instruction and Parent-School Relations.” Journal of Learning Disabilities 37(6):466-481.
Renée, B., Louis, C. & Hallahan, P., (2002). Identification of learning disabilities: research to practice. London: Routledge.
Sharma, M. (1999). Dyslexia, Dyscalculia and other Mathematics Problems. London: Routledge.


