Cross-Sectional Study
The study would utilize a cross-sectional design in examining the effect of job enrichment on job resources under the mediating influence of behavior roles. Since the study aims to collect data from diverse employees, this design is appropriate because it captures diverse attributes related to demographic information and varied elements of the job. The cross-sectional method is a research design that enables the collection of data from respondents at a particular time of interest (Creswell & Creswell, 2017). Moreover, the proposed design is relevant in the creation of scales, the collection of quantitative data, and hypothesis testing. In this case, the study plans to use scales of job enrichment, job resources, satisfaction, involvement, commitment, burnout, and motivation. Additionally, the study would collect quantitative data and test the hypothesis to determine the effect of job enrichment on job resources with the consideration of the mediating impacts of behavior roles. The collection of quantitative data permits the determination of the reliability and validity of outcomes.
When compared to other research designs, the cross-sectional method has some advantages. According to Creswell and Creswell (2017), this strategy is advantageous since it is not only simple but also cheap to administer to a large number of respondents. As the study targets a population of 500 employees, the design allows researchers to collect a representative sample with minimal costs. Another advantage of the method is that it can collect data using multiple variables with a high level of validity and reliability (Brase & Brase, 2017). Since the cross-sectional design does not also require follow-up, it does not encounter the challenge of respondent attrition due to an extended duration of the study (Tanner, 2016). Thus, the study seeks to collect data that is not only valid but also reliable from a representative sample of employees.
Sampling Method
The study would employ the stratified sampling method in the collection of data from the target population of 500 employees. This method is suitable because employees come from various industries with different working conditions. Flick (2020) asserts that stratified sampling is beneficial as it assures the representation of all groups in the target population. Since employees work in diverse industries, stratified sampling enables their clustering according to their unique work environments to augment representation. The stratification of data would prevent the occurrence of over- or under-representation of employees from specific industries. The target industries of the study are technology, manufacturing, retail, mining, service, construction, transport, and health industries. By ensuring that the data collected come from different industries, the study would boost the external validity of the findings. Gravetter and Wallnau (2017) add that stratified sampling classifies data into strata and allows comparison and establishment of patterns in populations. In this case, it is possible to compare variations of employees’ attributes according to their industries.
Furthermore, the stratified sampling method entails the randomization in the selection process to avert the negative effects of a researcher’s biases. Elliott and Woodward (2015) explicate that simple random sampling (SRS) diminishes the selection bias by assigning each individual in the target population equal probability. In each stratum of the target population, the study would apply SRS to ensure unbiased selection of respondents and the collection of valid data. Based on sampling frames, which consist of the list of employees in each industry, the study would generate random numbers and use them in the selection of an unbiased sample of employees. Subsequently, the study would administer the questionnaire to the selected employees to collect demographic information and data relating to job enrichment, job resources, and mediating behavior roles.
Measuring the Effect
In the regression analysis, the study would examine if the R statistic and R-square suggest the presence of a strong relationship and account for the variations in job resources. The study would also observe if the regression model is meaningful in predicting the effect of job enrichment on job resources with mediating effects of satisfaction, involvement, commitment, burnout, and motivation. A variable qualifies to have a mediating effect when it makes a predicting variable insignificant (Pallant, 2016). Ultimately, the coefficients of regression would indicate whether the job enrichment and mediators are statistically significant predictors of job resources.
Sample Size Calculations
The sample size would be calculated using the apriori method using the F-test and the fixed model of the linear multiple regression analysis in G*Power software. The input parameters that would be used are large effect size (f2 = 0.35), the error probability of 0.05, power of 0.95, and the number of predictors is 6. According to Stangor (2014), values of 0.02, 0.15, and 0.35 represent small, medium, and large size effects, respectively. The large effect size would be used because the study predicts that the dependent variables have strong relationships with the dependent variable. The probability of 0.05 would be used to reduce the likelihood of committing the type 1 error in hypothesis testing. According to Field (2017), an alpha level of 0.05 is reliable in preventing the rejection of a true null hypothesis in the analysis of inferential statistics. The study applied a power of 0.95 to limit the probability of committing the type II error in regression analysis. The power of analysis is one minus the probability of error (1 – 0.05 = 0.95), which is the likelihood of failing to reject an untrue null hypothesis (Jackson, 2015). In the multiple regression model, the study would utilize the six predictors comprising the independent variable and five mediators.
The outcomes of G*Power analysis (Table 1) indicate that the sample size of 67 employees is representative of the 500 population with a large effect size and power of 0.95, six predictors, and a critical F-statistic of 2.25. Therefore, the study would stratify 67 employees into industries of interest and employ simple random sampling in their selection.
Table 1. Outcomes of G*Power Analysis
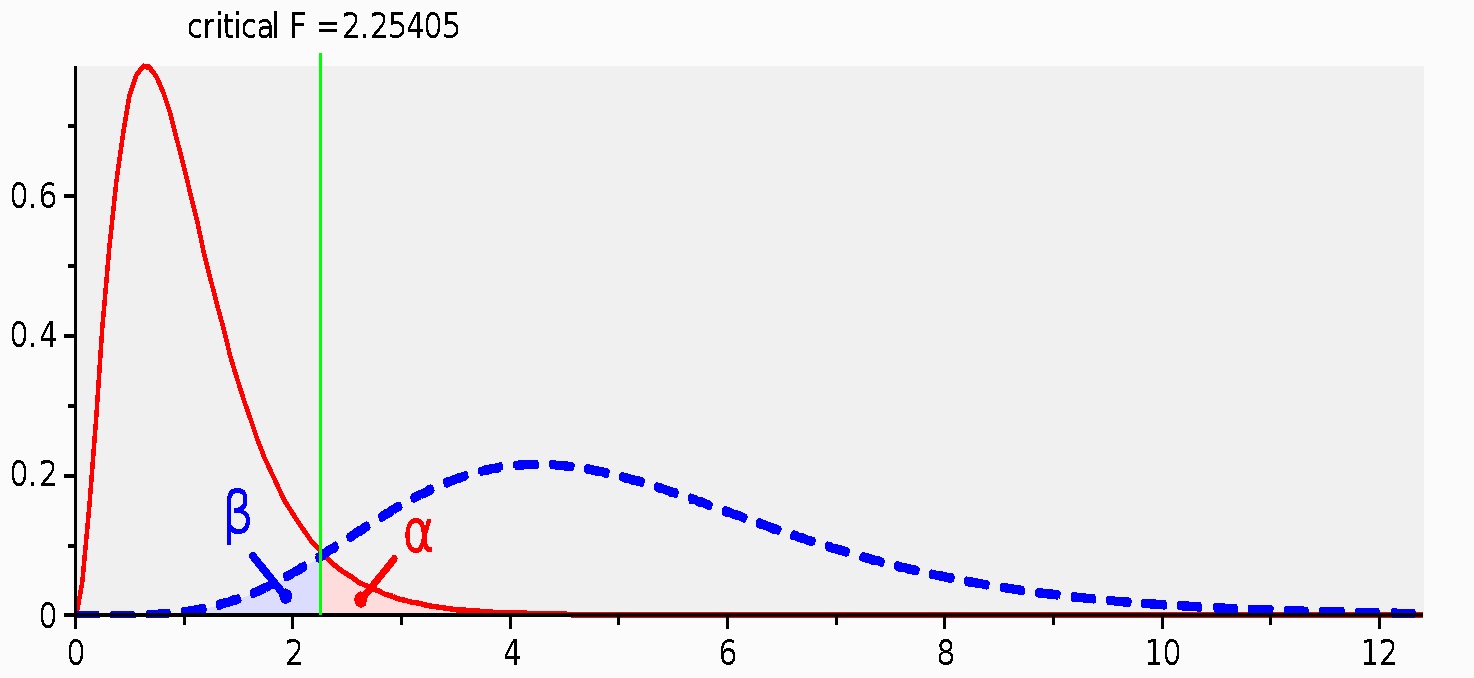
Figure 1 shows the probability density distribution of type I (α) and type II (β) error in hypothesis testing. These errors intersect at the critical F-static value of 2.25, which is a threshold for hypothesis testing. Inferential analysis suggests that F-statistic that is greater than 2.25 requires a rejection of a null hypothesis. At the same time, F-statistic that is less than the critical value needs the acceptance of the hypothesis.
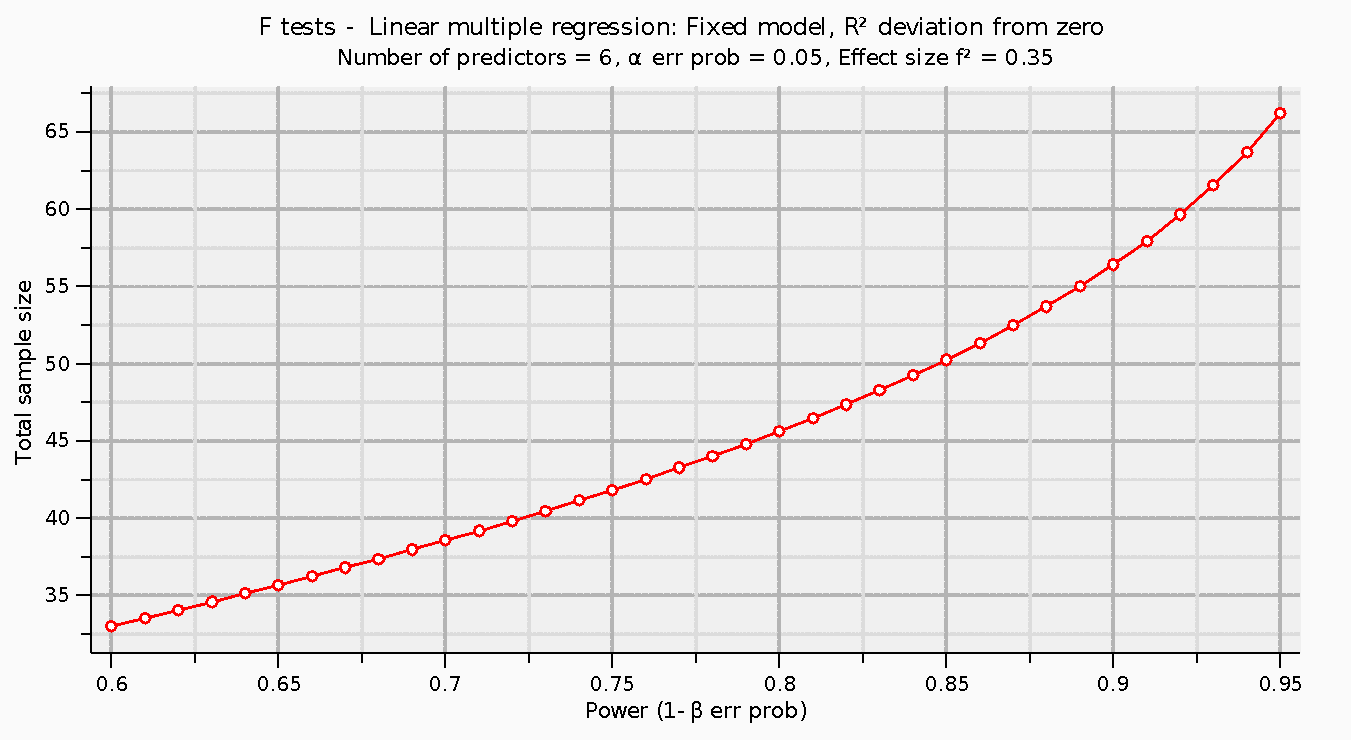
Further analysis (Figure 2) indicates that the sample size increases with the magnitude of power. For instance, a power of 0.85 gives a sample size of 50 employees, whereas the power of 0.95 generates a sample size of 67 employees.
References
Brase, C. H., & Brase, C. P. (2017). Understandable Statistics: Concepts and methods. Brooke.
Creswell, J. W., & Creswell, J. D. (2017). Research design: Qualitative, quantitative, and mixed methods approach. SAGE Publications.
Elliott, C., & Woodward, A. (2015). IBM SPSS by example: A practical guide to statistical data. SAGE Publications.
Field, A. (2017). Discovering statistics using IBM SPSS statistics (5th ed.). SAGE Publications.
Flick, U. (2020). Introducing research methodology: Thinking your way through your research project. SAGE Publications.
Gravetter, F. J., & Wallnau, L. B. (2017). Statistics for the behavioral sciences. Cengage Learning.
Jackson, J. (2015). Research methods and statistics: A critical thinking approach (5th ed.). Cengage Learning.
Pallant, J. (2016). SPSS survival manual: A step-by-step guide to data analysis using SPSS (6th ed.). Open University Press.
Stangor, C. (2014). Research methods for the behavioral sciences. Cengage Learning.
Tanner, D. (2016). Statistics for the behavioral & social sciences (2nd ed.). Bridgepoint Education.