Introduction
The goal of this project is to come up with a model that relates to the poverty level in the United States and the unemployment rate and total household income. The data that was used was of a time series nature. The data used is for the period between 1994 and 2011. This data will allow us to create a model that estimates the significance of the unemployment rate and level of household income on the poverty level. The data will be analyzed using multiple regression analysis with two independent variables. The data will be estimated using Eviews statistical software. The software will help in creating an equation. The equation will then be tested for Normality, Misspecification, Autocorrelation, and Homoscedasticity. These properties relate to the assumptions of the Ordinary Least Square method (OLS) of estimation. These assumptions must always hold for the method to be trusted in estimating a regression equation. When any of these assumptions, like in the case of misspecification, non-normality, Autocorrelation, and heteroscedasticity, a remedy has to be devised before the method can be used. The individual series also need to be tested for normality.
Testing for Normality
PR
For the poverty rate, the histogram drawn seems to be bell-shaped. This shows a sign of normality.
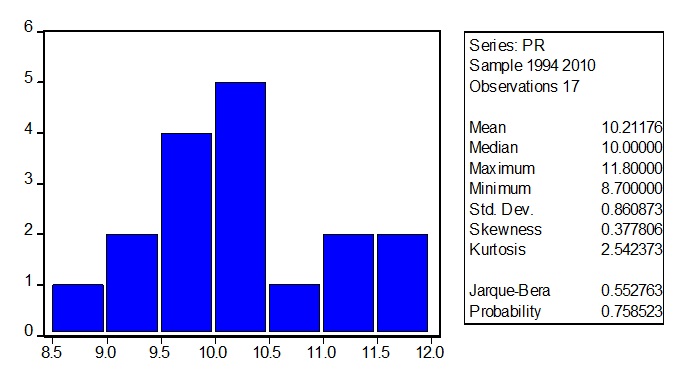
The test of normality is validated using the Jarque-Bera test which is shown below. To make inferences on this test, the level of significance is assumed to be α = 0.05. The decision criterion is that if the probability of the test is greater than the level of significance, then we do not reject the null hypothesis. The hypotheses being tested are as follows:
- Ho: S = (K-3) = 0 Meaning that the series is normally distributed.
- H1: S≠0, (K-3) ≠ 0 Meaning that the model is not normally distributed.
In the case of PR, the probability of Jarque-Bera (0.758523) is greater than the level of significance (0.05). The level of significance is, therefore, accepted. The conclusion is that the series is normally distributed.
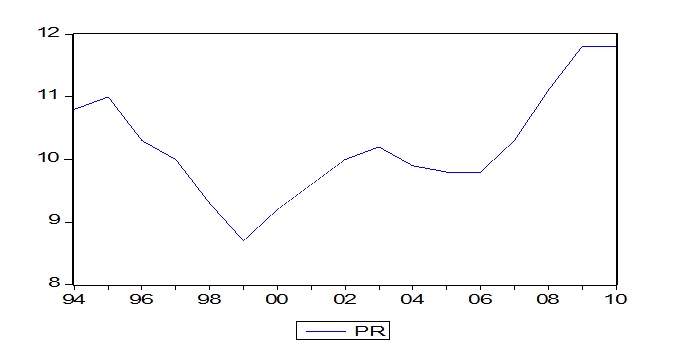
MHHR
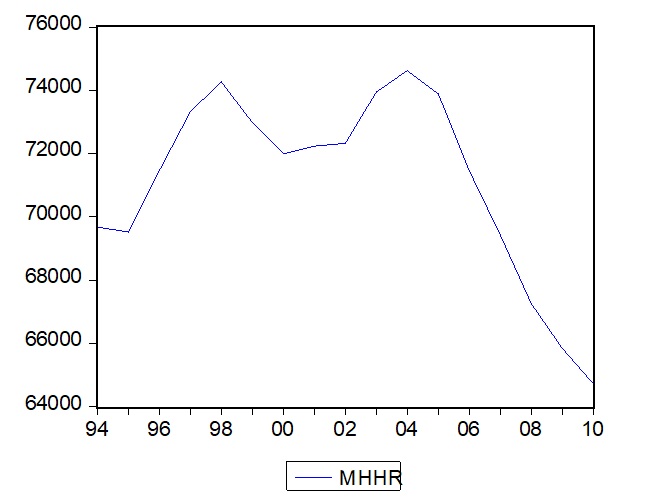
The results above reveal that MHHR is normally distributed. Firstly, the curve is bell-shaped and the histogram showed that there is a normal distribution. The Jarque-Bera test also revealed that there is normality. The probability of the Jarque-Bera (0.360337) test is greater than the level of significance (0.05). The null hypothesis is, therefore, accepted and the conclusion made that the series is normally distributed.
UR (Unemployment Rate)
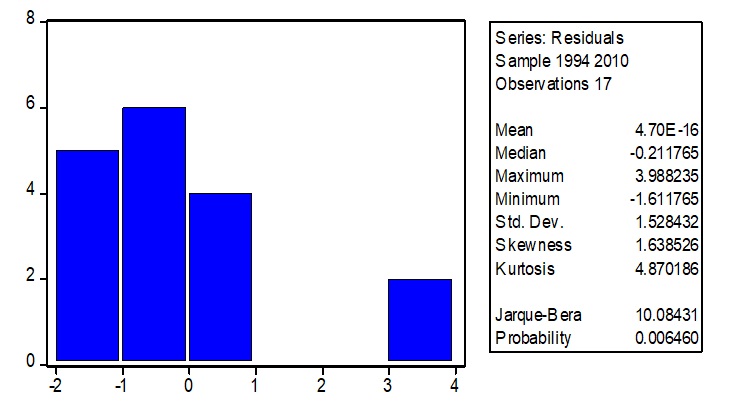
Concerning the Unemployment rate, the probability of the test is less than the level of significance, meaning that the series is not normally distributed.
Equation Estimation
The regression analysis is meant to estimate an equation where the poverty rate (PR) is the dependent variable and unemployment rate (UR) and mean household income (MHHR) are the independent variables. The variables are believed to have a linear relationship represented by the following model: PR = β0 + β1UR + β2MHHR + U. PR represents poverty rate, UR represents unemployment rate and MHHR represents the mean household income. U represents the stochastic term or the error term. The error terms the deviations of the individual data element from the line of best fit. The output given by Eviews is as follows:
The Equation will be estimated as follows: PR = 18.03288 + 0.295439 UR – 0.000133 MHHR.
We should test the significance of the independent variable on the dependent variable as follows:
PR = 18.03288 + 0.295439 UR – 0.000133 MHHR
SE = 3.635307 0.088749 4.57E-05
T-Statistic= 4.960485 3.328933 -2.914788
This test aims to investigate whether UR and MHHR are important determinants of PR.
Testing for the significance of UR
The hypotheses to be tested in this case are stated as follows:
For
H0: β = 0 => UR is not a significant determinant of PR. This is the null hypothesis.
H1: β ± 0 => UR is a significant determinant of PR. This is an alternative hypothesis.
Tests are done at a 95% level of confidence, meaning that the level of significance α is 0.05. The degrees of freedom (n-k) are 17-2 = 15. The value of the critical value of t at this point is 2.131. The decision rule is that if the t-statistic is greater than the t-critical, the null hypothesis is rejected. For UR, the t-statistic is greater than the t-critical. The null hypothesis is, therefore, rejected. The conclusion is that UR is an important determinant of PR.
Testing for the significance of MHHR
The following hypotheses are tested:
H0: β = 0 => MHHR is not a significant determinant of PR. This is the null hypothesis.
H1: β ± 0 => MHHR is a significant determinant of PR. This is an alternative hypothesis.
At α = 0.05 and df = 15, the critical value of t from the table is 2.131. The value of the t-statistic (2.914788) is greater than the value of the t-critical (2.131). In this case, the null hypothesis is rejected and the conclusion made that MHHR is an important determinant of PR.
Test for overall significance
This tests if all independent variables are jointly important determinants of the dependent variable. In this case, F-test is used. The value of the P-value for the F-statistic is used to suffice the decision rule. The decision criteria are that if the p-value is less than or equal to α, the null hypothesis is rejected. The hypotheses tested are stated as follows:
H0: β1 = β2 = 0. This is the null hypothesis that the variables are jointly/all insignificant.
H1: β1 ≠ β2 ≠ 0. This is the alternative hypothesis that at least one of the variables is significant. In the case above, the p-value (0.000003) is less than α (0.05). The null hypothesis is, therefore, rejected. The conclusion is made that the variables are not all insignificant.
Diagnostic Tests
All the variables in the model above were found to be significant. However, before the model is used, some tests need to be done. These are the tests of neutrality and efficiency. These tests are used to verify if the method of Ordinary Least Square (OLS) is strictly complied with while estimating the equation. The tests are used to find out whether the assumptions of OLS are fulfilled by the data collected for analysis. These tests are discussed below.
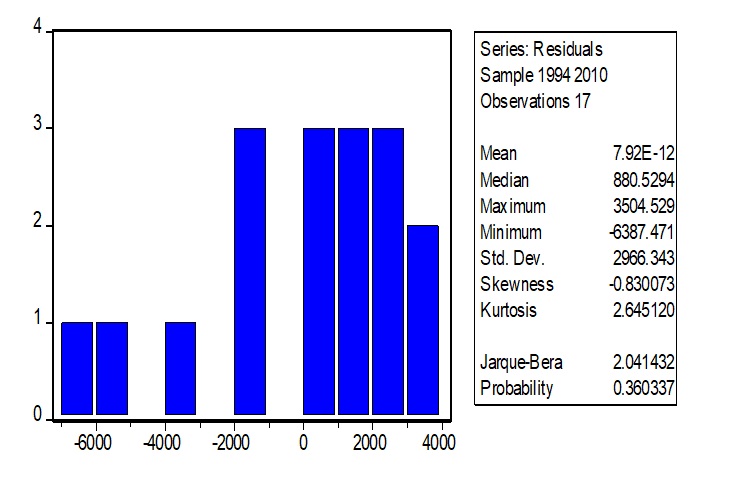
Test For Normality
This test is used to determine the model is normally distributed or not. The OLS assumption for normality is that ε t~ N (0, δ2). In this case, the mean of the sum deviations from the fitted line is zero and variance is constant (δ2). This test uses the Jarque-Bera Test.
The hypotheses tested in this test are as follows:
Ho: S = (K – 3) = 0 meaning that the model is normally distributed
H1: S ≠ 0, (K-3) ≠ 0 meaning that the model is not normally distributed.
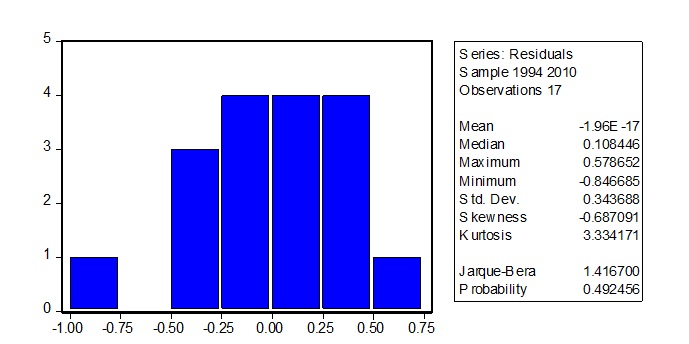
The test compares the probability for the Jarque-Bera Test and the level of significance. The level of significance, in this case, is 0.05 and the probability is 0.492456. The decision rule, in this case, is that if the probability of the Jarque-Bera Test is greater than the level of significance, the null hypothesis is not rejected. In this case, Probability (0.492456) > α (0.05), meaning that the null hypothesis is not rejected. The conclusion is that the model is normally distributed.
Test for Misspecification
For a model that is well specified, the expected value of the error term is equal to zero (that is E (εt) = 0). The test involves Ramsey RESET Test whose output from Eviews is given as follows:
From the restricted regression equation estimated above, we estimate the unrestricted regression model as stated below: PR = 18.03288 + 0.295439 UR – 0.000133 MHHR + c1e^2 + c2e^3 + c3e^4 + ut. The hypotheses tested are as follows:
Ho: c1=c2=c3=0 meaning there is misspecification
H1: c1≠0, c2≠0, c3≠0 meaning there is no misspecification.
The probability of the Ramsey RESET Test is less than the level of significance and, therefore, we reject the null hypothesis. We, therefore, conclude that there is no misspecification by accepting the alternative hypothesis.
Test For Autocorrelation
This test is aimed to investigate whether the error terms are independent across all observations. The desired observations are that the error terms are not correlated and their covariance is zero. That is cov (εt, εj) =0. This investigation involves conducting a Bruesch-Godfrey Serial Correlation LM Test. The Eviews results are as follows:
The null hypothesis is that there is no autocorrelation while the alternative hypothesis is that there is a presence of autocorrelation. The decision criterion is that if the P-value or probability of Breusch-Godfrey Serial Correlation LM Test is greater than the level of significance we do not reject the null hypothesis. In this case, the p-value (0.072335) is greater than the level of significance (0.05). The null hypothesis is, therefore, accepted. The conclusion is that there is no autocorrelation. This also means that there is no serial correlation problem in the data.
Test for Homoscedasticity
To test the presence of homoscedasticity, we shall use the White Heteroscedasticity Test. The desired results, in this case, are that the error term has constant variance across all observations. That is var (εt) = δ2. The hypothesis that we will test is stated as follows:
- H0: Residuals are homoscedastic.
- H1: Residuals are heteroscedastic.
The decision criterion is to compare the p-value of Obs*R-squared with the level of significance (0.05). If the P-value is greater than the level of significance, then we accept the null hypothesis. The Eviews output for White Test are as follows:
The probability of White Heteroskedasticity Test Obs*R-squared is 0.754820, while the level of significance is 0.05. This makes it impossible to reject the null hypothesis. The null hypothesis is accepted and the alternative hypothesis is rejected. The conclusion is that the residuals are homoscedastic. The variance of the residuals is constant on all observations.
Conclusion
The study involved testing whether the poverty level in the United States is dependent on the unemployment rate and total household income. The investigation was done using multiple regression analysis. Firstly, the series were tested for normality. The PR and MHHR series were found to be normally distributed. The UR series, however, was not found to be normally distributed. The regression analysis was then conducted to investigate the relationship between the variables. Eviews program was used to conduct the analysis. The regression equation was estimated as follows: PR = 18.03288 + 0.295439 UR – 0.000133 MHHR. The variables UR and MHHR were found to be important determinants of PR. The coefficients α1 and α2 we found to be significant. A 1% increase in the Unemployment rate led to a 29.55% increase in poverty level assuming that all the other factors are held constant. A 1% increase in Mean Household income led to a decrease in the poverty level by 0.0133% assuming all the other factors are held constant. The coefficient of determination (Adjusted R squared) showed that UR and MHHR jointly explained 81.7845% of the variation in PR. The tests conducted on the model revealed that the model is unbiased and efficient. The model passed the test of Normality, Misspecification, Autocorrelation, and Homoscedasticity according to the tests that were conducted.