Introduction
The experiment was composed of two investigations. The main areas of concern were to carry out an examination test on the status of waves on a string. The research aimed at observing the relationship between string and wave speed. Further, the research would also look at the speed of string waves in an air column and identify the degree of the sound pace. Each investigation had a different mode of research activity. The apparatus used were a 120Hz vibrator, three-rod clamps, a metric stick, three turning forks that had particular frequencies, two stands with rods and brass weights, and valid wave indicators. The apparatus helped in undertaking graphical analysis through the use of wavelength, duration of the waves, and graphical analysis.
Investigation 1
Setup and procedure
In the first research, we were to carry out an experiment to identify the stand waves on a string. Thus, we first set rods about a meter other than each one-of-a-kind. In our next step, we linked the two rods by use of a string. On one end of a string, we connected a bucket, and the other forestall of the string became the opportunity rod on which we clamped the electromagnetic vibrator and the string holder. The particular rod had a pulley through which the string was handed, and the bucket became hanging (Hyde & Batishchev, 2018). As the studies modified into set up, we then switched the vibrator on, due to which the string began to vibrate, and we were able to see the best style of nodes at the string. To get the various number of nodes, we commenced adding brass weights to the bucket, and so we recorded the space among nodes for three, four, five, six, seven, and eight styles of nodes. Using the values of the ones, we additionally calculated the usual distance, the wavelength, the velocity, and the tension within the string. Lastly, calculating the values of the ones, we executed a graph using the charge squared and the tension pressure of the string to get the mass constant with the unit length of the string.
Data and analysis
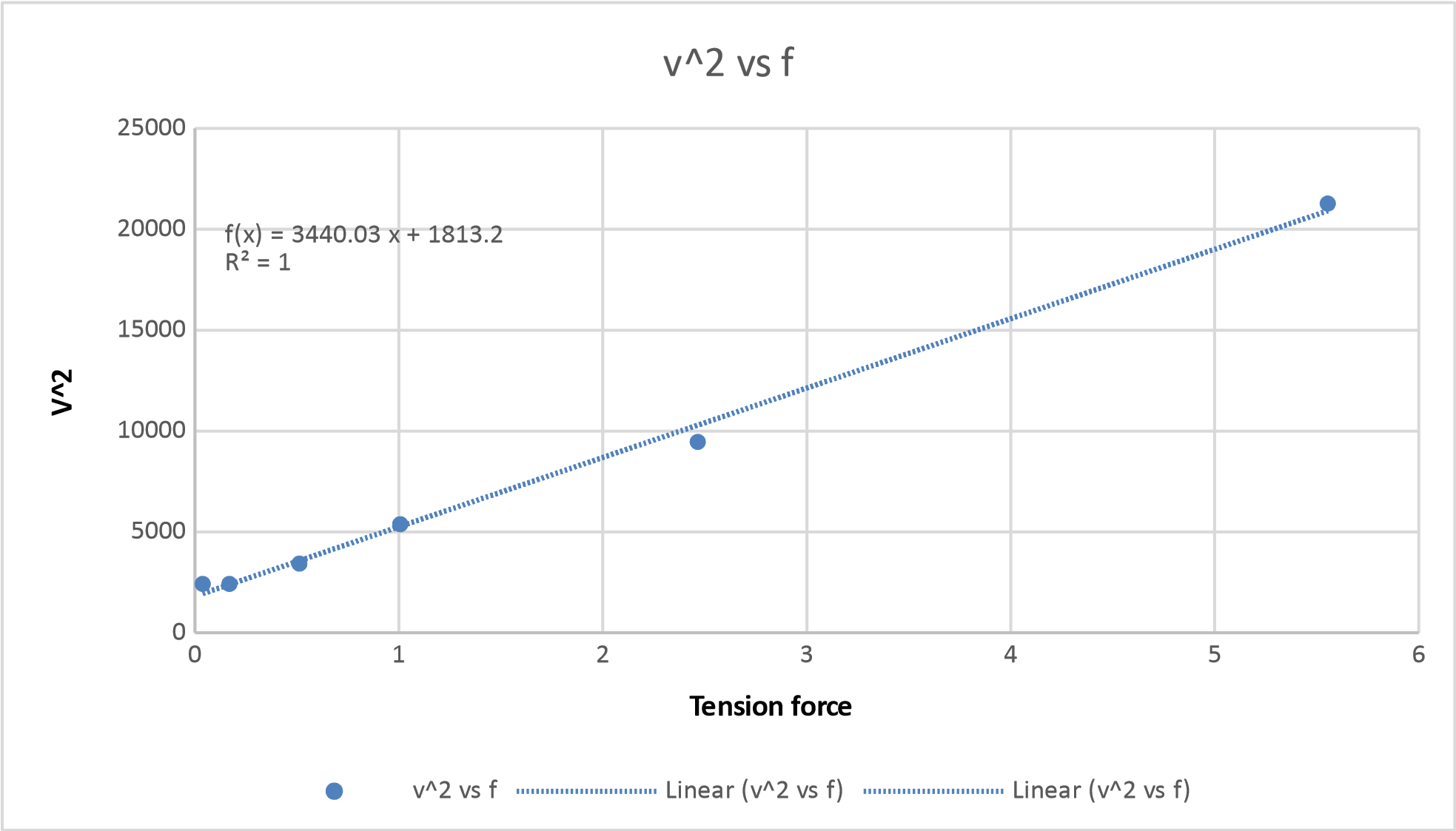

The wavelength of the nodes was then found by multiplying this distance by 2. The error in the wavelength, as calculated by the ruler, was ± 0.0005 m. As we had the wavelengths, we calculated the speed of the wave using
v = λf
The frequency of this investigation was 120 Hz, and I had different values for the wavelength, due to which we were able to calculate speed, and the error in the speed was calculated using the formula:
σv = (v*σT)/ (2T)
We also found the tension in the string by multiplying the mass and the acceleration due to gravity. The error in this force was equal to that of the wavelength shown by the ruler, which was ±0.0005m.
Then using the graph above, we found the mass per unit length by using the equation:
v = (T/μ) 0.5
The string density we found came out to be 0.28689, but the actual density of the string was 0.32
Investigation 2
Setup and procedure
For this investigation, the creation of standing longitudinal waves was essential. We then started to observe and note the position in which the sound was heard was the loudest. We repeated the process three times by tuning forks of different frequencies. We then measured these values, which helped us find the period, wavelength of the wave, and speed of the sound. The graph was created by using the period and the wavelength.
Data and analysis

The average speed of sound: is 341.62
It was calculated by adding all the speeds of sound and then dividing by three.
Conclusion
Investigation 1
- Calculated String Density: 0.28689
- Theoretical String Density: 0.32
The errors within the calculated and the theoretical value may be brought on due to the parallax errors as it is miles very tough to rely upon the number of nodes as the variety increases. It is also challenging to look at wherein the node begins and ends, which causes the space between the nodes to be uncertain.
Investigation 2
- Calculated speed of sound: 341.62 m/s
- The theoretical value was: 343 m/s
The calculated value is nearing the theoretical cost, and the error that would have resulted in this arising will be the way the dimension became fingered because it was no longer clean to measure the location correctly wherein the loudest sound turned into produced.
Reference
Hyde, A., & Batishchev, O. (2018). Undergraduate physics laboratory: Electrophoresis in chromatography paper.American Journal of Physics, 83(12), 1003-1011. Web.