
Summary
This guide describes how to set up and perform experiments related to the deflections and reactions of a rectangular portal. The equipment clearly demonstrates the principles involved and gives practical support to your studies.
Description
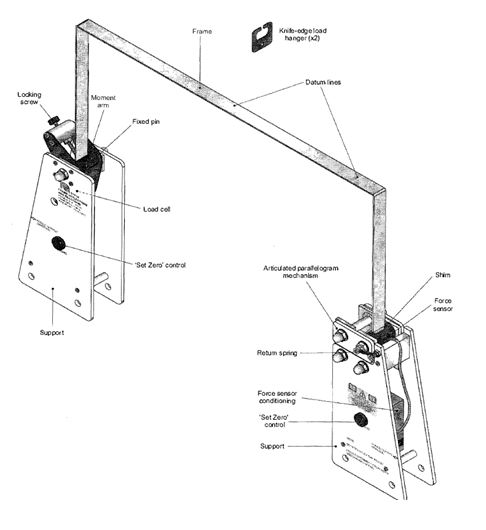
Figure 1 shows the Frame Deflections and Reactions experiment. It consists of two supports (or springing) and either a uniform or non-uniform section aluminum alloy portal frame. The left-hand side of the portal is pinned to its support and is restrained from turning by a moment arm. The moment arm contacts a load cell, so, measuring the restraining moment. The right-hand side of the portal fixes to a mechanism which prevents rotation but allows movement in the horizontal direction against a second load cell. The load cell reacts and so measures the horizontal reaction produced by the portal. A digital indicator positioned at the top corner of the portal measures the sway (horizontal movement). Vertical loads are applied to the portal using a knife-edge hanger and masses.
In the experiments, we will use measured and calculated values of moments, reactions and sway to study the linear elastic behavior of the portal, the sway of the frame due to the asymmetry of the frame or the loading position.
How to Set Up the Equipment
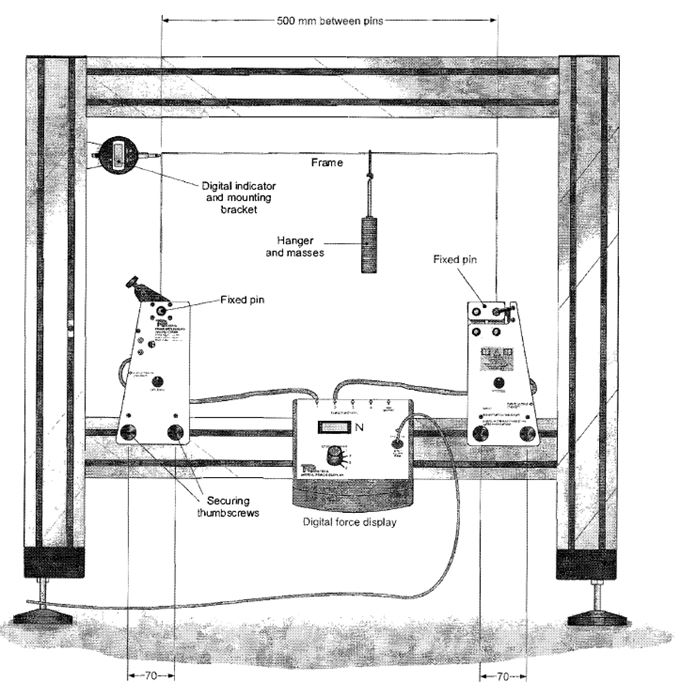
The Frame Deflections and Reactions experiment fits into a Test Frame. Figure 2 shows the Frame Deflections and Reactions experiment in the Structures Test Frame. Before setting up and using the equipment, always:
- Visually inspect all parts (including electrical leads) for damage or wear. Replace as necessary.
- Check electrical connections are correct and secure. A competent person must only carry out electrical maintenance.
- Check all components are secured correctly and fastenings are sufficiently tight.
- Position the Test Frame safely. Make sure it is on a solid, level surface, is steady, and easily accessible.
(Never apply excessive loads to any part of the equipment.)
The following instructions may have already been completed for you. If so, go straight to Section 2.
- Place an assembled Test Frame (refer to the separate instructions supplied with the Test Frame if necessary) on a workbench. Make sure the ‘window’ of the Test Frame is easily accessible.
- There are four securing nuts in the top groove of the bottom member of the frame. Slide them to approximately the positions shown in Figure 2.
- Fit the left-hand support to the frame using two thumbscrews (on the front only) into the frame securing nuts.
- Fit the right-hand support in roughly the correct position and fasten as per the left-hand support.
- Adjust the position of the right-hand support until the distance between the pivots is 500 mm.
- Fit the uniform portal frame to the pivots using two shims on each side. Ensure the frame is secure by tightening the grub screw at each end.
- Referring to Figure 2, mount the digital indicator onto the back of the Test Frame. Ensure that there is at least 3 mm of travel in each direction. If there is not fine adjust the positions of the two supports, maintaining the 500 mm between centers.
- Check the frame is square and true on the supports; adjust the supports if required.
- Make sure the Digital Force Display is ‘on’. Connect the mini DIN lead from ‘Force Input 2’ on the Digital Force Display to the socket marked ‘Force Output (Thrust)’ on the right-hand side of the support. Connect a second mini DIN lead from ‘Force Input I’ to ‘Force Output (Moment) on the left-hand support.
- Undo the knob securing the dial indicator and swing it away so that the contactor no longer touches the portal frame. Carefully zero the force meter using the dial on each support of the experiment for both inputs (use the selector switch to view the appropriate input). Gently apply a small load with a finger to the center of the frame cross member and release. Zero the meter again if necessary. Repeat to ensure the meter returns to zero.
Note: If the meter is only ±0.l. N, lightly tap the Test Frame (there may be a little ‘stiction’ and this should overcome it).
Experiment 1: Analysis of a No-Sway Portal Frame
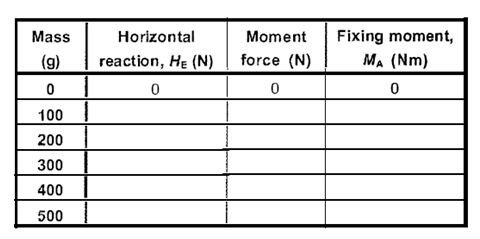
In this experiment, we will apply increasing vertical load to the centre of the uniform portal frame and investigate how this affects the horizontal reactions and fixing moments. You may find the following table useful in converting the masses used in the experiments to loads.
Table 1: Grams to Newtons conversion table
Undo the screw on the reverse of the digital indicator and swing it 90° clockwise so the contactor no longer touches the frame (it is not required for this experiment). Position a knife-edge hanger in the center of the frame cross-member. A line indicates the center. Ensure that the force meter reading is zero, and then put a mass (on a hanger) of 100 g on the knife-edge. Record the resulting force meter readings for the ‘moment’ and ‘thrust’. Increase the mass in 100 g increments. Record the force meter readings for each increment in Table 2. Using the Vernier provided, accurately measure the section of the frame and calculate the second moment of area of the section. Make a note of this value.
Table 2: Results for Experiment 1
Analysis and Calculations
Calculate the moments from the moment force by multiplying it by the length of the moment arm (0.05 m) complete Table 2.
Plot graphs of the moment and horizontal reaction against the applied load (convert the mass to a load in Newtons).
The relationship between the horizontal reaction and the load as shown in the graph is a linear positive relationship. Notably, as the horizontal force increases, the load also increases by a linear- positive factor of force. However, the relationship between the moment of force and the load is a non-linear negative relationship. In this case, a positive moment of force corresponds to a non-linear negative factor of load. At a load of 4.9N from the graph, the horizontal and moment forces are 0.98N and -0.18N respectively.
State the nature of the relationship between the moment and horizontal reaction and the load. Read off values for a load of exactly 4.9 N.
Sketch the detected shape of the frame below:
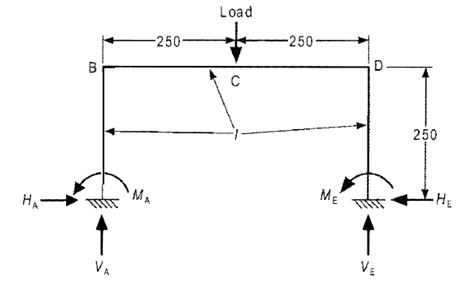
Use static equilibrium and the symmetry of the frame to calculate values for the vertical reactions, VA and VE.
- Vertical reactions, VE for 100g
Moment about A
VEx (0.025m+0.025m)-0.49Nx0.025m-0.98NX0.025m=0
VE=0.735N
Therefore, Vertical reaction, VA:
VA=0.98N-VE
VA=0.245N
- For 200g
Moment at A
VEX0.05-0.98NX0.025m-1.96NX0.025m=0
VE=1.47N
Therefore, VA
VA=1.96N-VE
VA=0.49N
- For 300g
Moment at A
VEX0.05-1.47X0.025-2.94NX0.025=0
VE=2.205N
Therefore, VA
VA=2.94N-VE
VA=0.735N
- For 400g
Moment at A
VEX0.05-1.96X0.025-3.92X0.025=0
VE=2.94N
Therefore, VA
VA=3.92N-VE
VA=0.98N
- For 500g
Moment at A
VEX0.05-2.45X0.025-4.9NX0.025=0
VE=3.675N
Therefore, VA
VA=4.9N-VE
VA=1.225N
Using Static equilibrium, calculate the horizontal reaction and moment reaction at points A and E.
Reactions for both horizontal and moments at 100g
Sum of Moment at E=0 (Hibbeler, 2020)
0.735×0.025-0.98xEx=0
HE=0.01875N
However,
+ sum of Fx=0
-Mf-0.01875+0.025×0.49=0
Mf=0.0065N
At 200g
HE=0.01875N
However,
+sum of Fx =0
-Mf-0.01875+0.025×0.98=0
Mf=-0.00575N
At 300g
HE=0.01875N
However,
+sum of Fx=0
-Mf-0.01875+0.025×1.47=0
Ax=-0.018N
At 400g
HE remains constant= 0.01875N
However,
SUM of Fx=0
-Mf-0.01875+0.025×1.96=0
Mf=-0.03025N
At 500g
HE remains constant= 0.01875N
However,
Sum of Fx=0
-Mf-0.01875+0.025×2.45=0
Mf=-0.0425N
Do your results correspond favourably with theoretical answers? Comment on any discrepancies.
The experimental values of the results above do not correspond to the theoretical values. The difference in values may be due to the disparities of the diffusion voltage or the non-zero electric fields at the borders of the deflection machine. The diversity in the values could also results from errors in the deflection computation of flexural members of the frame deflection machine. Temperature affects the expansion of metals. In this regard, the room temperature could results in errors as they often lead to abnormal expansion of the aluminium alloy, which is used as the frame beam. Lastly, errors due to calibration of the frame deflection machine might results in experimental errors, hence differences in both the theoretical and experimental data.
Reference List
Hibbeler, R.C. (2020) Mechanics of materials. 8th edn. New York, NY: McGraw-Hill.