Experiment 1: Shear Force Variation with an Increasing Point Load
Calculate the theoretical shear force at the cut and complete the Table 2.
Calculations:
- Theoretical Shear Force (N)
Sc=w*a/L
Where L=0.44m
And a=0.26m.
- For 100g (0.98N)
Sc=w*a/L
Sc=0.98*0.26/0.44=0.579N
- For 200g (1.96N)
Sc=w*a/L
Sc= 1.96*0.26/0.44=1.158N
- For 300g (2.94N)
Sc=w*a/L
Sc=2.94*0.26/0.44 =1.737N
- For 400g (3.92N)
Sc=w*a/L
Sc=3.92*0.26/0.44=2.316N
- For 500g (4.9N)
Sc=w*a/L
Sc=4.9*0.26/0.44=2.895N
Plot a graph which compares your experimental results to those you calculated using the theory. Comment on the shape of the graph. What does it tell us about how shear force varies due to an increased load? Does the equation we used accurately predict the behaviour of the beam?
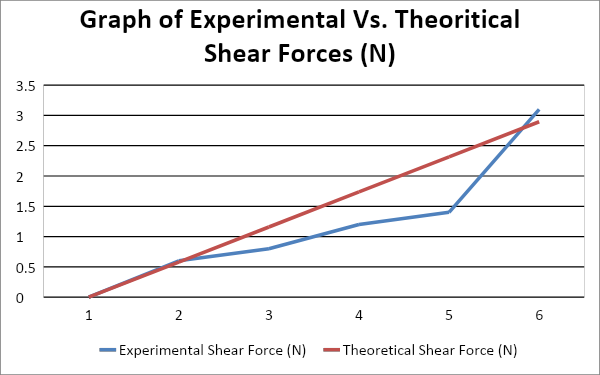
The shape of the graph shows a linear relationship between shear forces and the weight of material on the beam for experimental shear force. This means that for every increase in weight on the beam, there is a linear increase in shear force. However, for the experimental shear force graph, it indicates a nonlinear relationship, which creates a curved line on the graph. This could be attributed to such experimental errors as permanent deformation of the beams after long years of use. Despite the difference in shear forces between theoretical and experimental, the results do indicate that the equation used could predict the behavior of the beam, but not accurately predict it because of experimental errors.
Experiment 2: Shear Force Variation for Various Loading Conditions
Record the Digital Force Display reading in a table as in Table 3.
Calculate the support reactions (RA and RB) and calculate the theoretical shear force at the cut.
- For Figure 4
The algebraic total of the moments produced by the forces operating to the left or right of the cut determines the bending moment at the “cut.” Therefore;
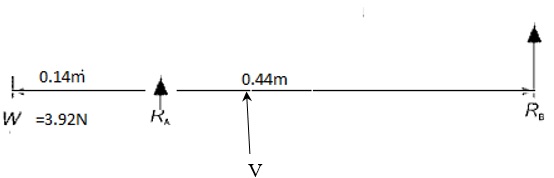
Mcut (moment at cut)
∑Fy=0
=RA+RB-W=0
=RA+RB-3.92=0………………………………………………………..Equation 1
∑MB=0=-(RAx0.44) +Wx0.58=0
∑MB=0=-(RAx0.44)+3.92×0.58=0……………………………….….Equation 2
-0.44RA=-2.2736
RA=5.17N
But;
RA+RB-3.92=0
RB=3.92-RA
RB=3.92-5.17
RB= -1.25N
Moment at cut
However, the product of the force being applied to the beam with respect to the cut between the fixed end of the beam and the force application point is the shear force moment.
Therefore, ∑fy=0
= V+RA-3.92=0
=V+5.17-3.92=0
= -1.2N
- For Figure 5
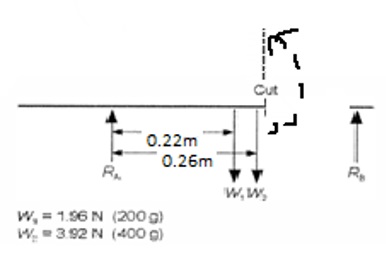
∑Fy=0
=RA+RB-W1-W2=0
=RA+RB-1.96 -3.92=0
=RA+RB-5.84=0………………………………………………………..Equation 1
Moment at B
∑MB=0=
-RAx0.44+1.92×0.22+3.92×0.18=0………………………..……….….Equation 2
-0.44RA+0.4224+0.7056=0
-0.44RA=-1.128
RA=2.564N
But; RB=5.84-RA
RB=5.84-2.564
RB=3.276N
However, shear force from the cut to balance the beam;
=∑fy=0
=∑fy = V+RA-W1-W2=0
V+2.56-1.96-3.92=0
V+2.56-5.88=0
V=5.88-2.56
V=3.32N
Therefore, the theoretical shear force is equal to 3.32N
For Figure 6
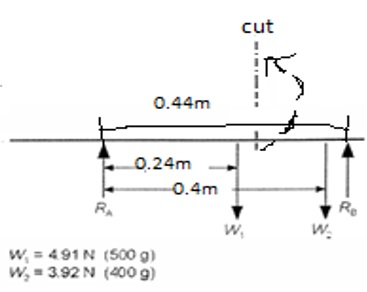
Mcut (moment at cut)
∑Fy=0
=RA+RB-W1-W2=0
=RA+RB-4.91 -3.92=0
=RA+RB-8.83=0………………………………………………………..Equation 1
Moment at B
∑MB=0
-RAx0.44+4.91×0.2+3.92×0.04=0………………………..……….….Equation 2
-0.44RA+1.1388
-0.44RA=-1.1388
RA=2.588N
But;
RA+RB-W1-W2=0
2.588+RB-4.91-3.92=0
RB=-8.83-2.588
RB=6.242N
However, theoretical shear force
=∑fy=0
V+RA-W1=0
V+2.588-4.91=0
V=4.91-2.59
V=2.32N
Comment on how the results of the experiments compare with those calculated using the theory.
The results of the experiments and those of the calculated figures using the theory were. For instance, in Figure 4, the experimental shear force is -1.4N, yet using theory to calculate the shear force, a value of -1.2N was obtained. Moreover, the results were different for both Figure 5 and Figure 6. For Figure 5, the experimental shear force obtained is 2.4N, yet its theoretical shear force is 3.32N. The results are also different in Figure 6, where the experimental shear force obtained is 1.9N as compared to its theoretical shear force of 2.32N. The difference in the experimental results and those from calculated theoretical figures could be as a result of experimental errors. Such errors may include using old beams that have undergone permanent deformation, errors in reading the shear forces, or errors due to room temperature that might result in the materials making the beams expand, hence wrong results.