Background
Inspired by the movie “Up” from the animation studio Pixar, people have begun to wonder whether it is realistic to bring a significant sci-fi invention to life. Specifically, it is about lifting a building, whether a private home or a skyscraper with commercial offices, high into the air using helium-filled balloons. Obviously, this task has no practical value since moving a building through the air between points raises a number of problems related to foundations, engineering, and economic considerations, as well as national security. In addition, it is very likely that the ultimate economic benefit of such an undertaking would be disproportionate to constructing precisely the same building at the destination point. Nevertheless, lifting hefty objects into the air is intriguing to the mind and of high scientific interest in terms of classical physical and mathematical calculations.
The present work assumes that even a large building can be lifted into the air using a large number of balloons. The most impressive building of the Burj Khalifa skyscraper, which has a height of 828 meters and a total mass of 500 thousand tons, was chosen for specification. The Burj Khalifa is located in the center of Dubai, which is located in the UAE. The key focus of the mathematical essay is to determine the minimum number of balloons that can lift the building into the air and consider the associated features of this event.
Some Assumptions
There are too many physical and logical variables that can impede calculations and make the entire study impractical. For the purposes of this mathematical essay, many of these variables are omitted for lack of use. For example, air resistance is not taken into account, and therefore it is assumed that balloons can theoretically rise infinitely high. In addition, balloons are assumed to be made of a material strong enough not to be ruptured by the change in pressure in the air. The balloons used are medium-sized, that is, their optimum diameter is 0.30 meters. It is also necessary to assume that the ball is perfectly spherical, which simplifies the mathematical calculation of its volume. Meanwhile, the theory of resistance of materials suggests that the basic materials for building a building, such as cement, wood, brick, or reinforced concrete, cannot withstand tensile loads. This means that if such a house is pulled upward by the upward force of balloon lift, it is more likely to break apart than to be lifted by monolithic blocks. The assumption that the Burj Khalifa is a solid building with no seams is another critical assumption.
Calculating the Number of Balloons
The basic idea of how balloons work is intuitively obvious: the greater the number of balloons used, the easier it is to lift a heavy object. This works perfectly with everyday objects: one can lift a writing pen with a few medium-sized balloons, and one can lift two pens with twice as many. In this context, lifting an entire building must be realized through a potentially massive number of balloons. Attempting to answer the question of how many are needed in theory must begin with determining the amount of gas that can fit in a single balloon. If elongated balloons were used, their volume could be calculated from the amount of water they would hold. However, the assumption of a spherical balloon shape allows the mathematics to be used. Equation (1) reflects the general formula for calculating the volume of a spatial ball shape. Given that the diameter of the balloon was given as 0.30 meters, the average volume of the balloon should be 0.01413 m3 or 14.13 liters.
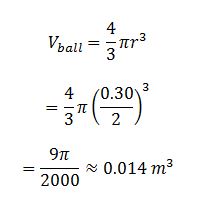
Once the volume of one balloon has been found, it must be pointed out that the combination of volumes will work according to the superposition principle. To put it differently, combining several balloons will cause the total volume of the entire structure to be numerically and equivalently equal to the total volume of all balloons. This assumption noticeably optimizes the calculations and allows one to almost increase the total volume of all balls simply infinitely by adding a new one.
Now it is necessary to discuss why a helium-filled balloon rises into the air in the same way that bodies remain floating in the water. Helium was chosen as the filling for balloons because it is one of the most obvious, and therefore most cost-effective, options with which to inflate flying balloons. The reason for this effect is the Archimedes force, but instead of classical water as a medium, in this case, there is pushing out by air, as shown in equation (3). The calculation shows that the Archimedean force for one average spherical ball is 0.168 N. However, this force is not the only thing that affects the ball in the air. Equation (4) shows calculations of weight (not mass) for the ball since it cannot be excluded that it has mass. It can be seen that the total weight is composed not only of the weight of the helium inside the balloon but also of the weight of the latex shell, i.e., the actual empty balloon. To be specific, the mass of the empty balloon was taken as two grams.
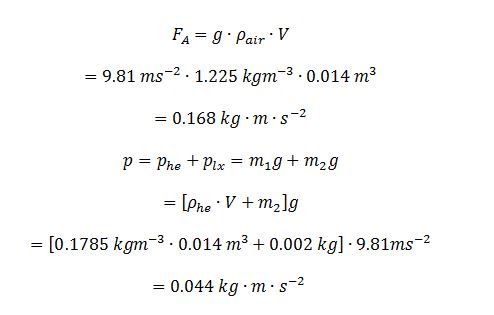
Thus, for a single ball, it is evident that its force is almost four times higher than the force that attracts it to the surface of the Earth. Then the total lifting force of one ball is calculated by subtracting one value from the other, as shown in equation (6). This data can be interpreted differently: one such ball can lift about 12.6 g.

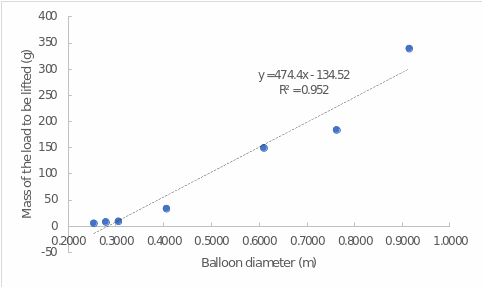
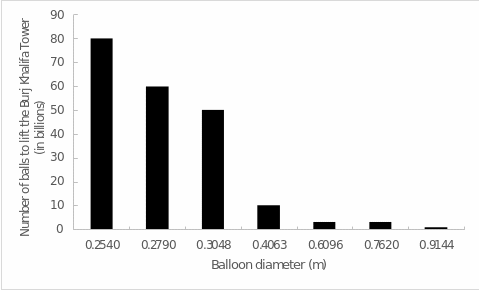
The obtained data correspond well to the accurate calculations for balloons. In fact, if one turns to the reference data, it becomes clear that the calculations for a 30-centimeter balloon are close to what is published. In addition, it can be seen that each of the balloon types has its own lifting force, which depends directly on the volume of helium alone. Figure 1 below shows this trend well, and the increase in mass of the lifted load as a function of balloon diameter can be called almost linear (R2 = 0.952).
The last action in the calculations is one of the easiest. It was known that the mass of the Burj Khalifa is equal to 500 thousand tons, or 500 billion kilograms. Since it is now clear that one balloon can lift a mass of 12.4 g, it is not difficult to determine the theoretical number of balloons that would be required to lift the entire skyscraper. The calculations are shown in detail in equation (7):
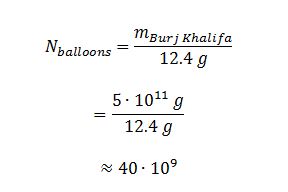
To put it another way, the simulations showed that it would take about 40 billion such medium-sized balloons to lift the Burj Khalifa skyscraper using balloons. It was fascinating to estimate how many other balloons (based on Figure 1) would be needed to lift such a tower. Thus, Figure 2 confirms the expectation: the larger the volume of balls used, the smaller the number required. For example, unlike an average ball of 30 centimeters, large balls with diameters of almost 1 meter will require 40-50 times less.
Finally, one can calculate the economic benefit of such an event using as input the cost of one latex balloon of the right size sold on Amazon. For example, the average cost of a batch of 100 balloons 30 centimeters in diameter is $17. Equation (8) shows that the number of packages needed is 400 million, which means the total cost of such a purchase would be nearly seven billion dollars. By comparison, Canada’s GDP for 2020 was four times less, at $1.6 billion. In addition, the construction of the Burj Khalifa Arab skyscraper cost $1.5 billion, which is still significantly cheaper than the proposed measure.
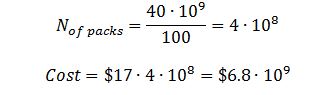
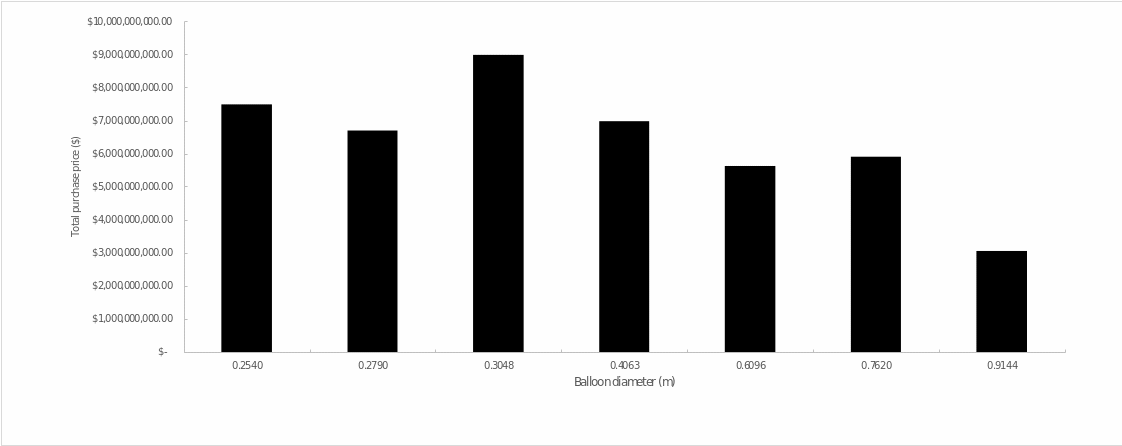
If one looks again at the different sizes (Figure 3), one can see that the cheapest purchase cost will be fair for the largest balloons, but it is still twice as much as the construction of the new Burj Khalifa tower.
Reference List
“Is Our Earth Getting Heavier With The Increase In Construction,” construction life cycle, para. 1, 2019. Web.
Ashish, “Why Does Concrete Have Great Compressive Strength, But Poor Tensile Strength,” scienceabc, para. 7, 2021. Web.
Al-Dahhan, W., and E. Yousif. “Hydrogen balloons: Bright colors but hidden fire hazard,” International Journal of Public Health & Safety, vol. 3, no. 1, 2018. Web.
“Balloon Lift Ability Chart,” balloon market, n.d. Web.
World Bank, “GDP (current US$) — Canada,” data world bank, 2021. Web.
Abraham, O. A. “Effective project management in contemporary developments: Case study Burj Khalifa tower,” IRE Journals, vol. 3, no. 2, 2019. Web.