Introduction
The in-depth study of complex compounds is a particular area of analytical instrumental chemistry that uses existing theories and practices to establish a substance’s formula. Standardly, complex compounds are considered to be the most problematic substances in which the central complexing atom (M) is chemically bonded to a certain number of ligands (L), which forms the coordination number as shown in the Equation 1. The compound’s entire inner sphere then combines with the outer sphere, usually represented by a metal ion or an acidic anion.
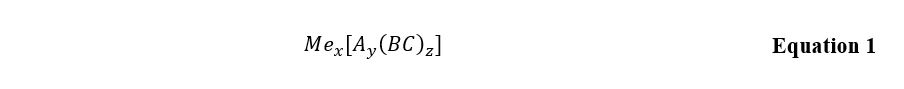
In analytical chemistry, there are several techniques for determining the formula of a complex compound, but in this laboratory work, the emphasis was on the applicability of Beer’s law, recognizing the fact that when a complex is formed, one of the substances is in excess. The following mass balance equations are characteristic of the inner sphere of the complex.:
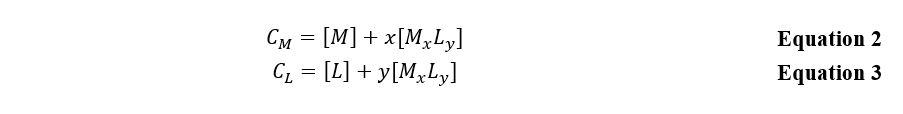
Consequently, if the ligand concentration is excessive, this leads to a negligible amount of the complexing agent, which can be excluded from the calculations. Then, applying this assumption to Beer’s law, the following expression for the optical density of the substance can be obtained:
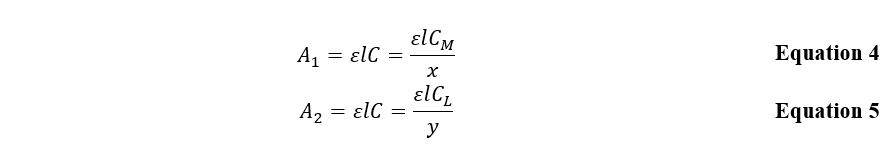
A similar expression, Equation 5, is characteristic for the situation when the complex-forming agent turns out to be an excessive amount. In both cases, the plot of the dependence of optical density on the substance concentration has a slope that depends on the complexing agent or ligand’s atomic amount. Then the ratio of these slopes is determined by the Equation 6 and is numerically equal to the ratio between the number of groupings in the inner sphere of the complex.
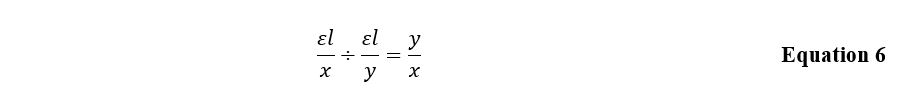
The above information forms the purpose for this laboratory study, in which the nature of the orange-red complex formed by the reaction between divalent iron and o-phenanthroline is investigated. By the spectroscopic study of a series of different solutions with excess iron and excess tricyclic organic at a wavelength of 515 nm, the relationship between the slope coefficients was established, and as a result, the ratios of atoms in the inner sphere of the complex were determined.
Experimental
Reagents
- Acetic Acid-Acetate Buffer, high purity
- Hydroxylamine hydrochloride,
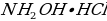, 10 % (w/v), high purity
Solutions
- stock iron(II) solution,
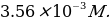A substance weighing 0.3589 g was dissolved successively in 50 mL of distilled water and 1.0 mL of concentrated hydrochloric acid, then diluted with distilled water to the 250 mL mark. - working standard iron(II) solution,
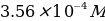. Transferring 25 mL of the prepared solution into a flask for dilution with distilled water to the 250 mL mark. - 1,10-phenanthroline solution,
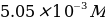. 0.0906 g of organic substance was dissolved in 70 mL distilled water heated to 75 ℃, and after cooling was quantitatively transferred to a 100 mL flask.
Procedure
Instrumental Methods of Analysis Chem 447 Winter 2020 manual experiment titled, Determination of the Formula of a Complex with the Slope-Ratio Method written by Judith Bazzi.
The procedure for this experiment was based on the methodological guide offered in this course. The experiment was based on the idea of creating a series of working solutions with different concentrations of divalent iron (five solutions in total) and o-phenanthroline (five solutions in total). Ten solutions were examined using ultraviolet spectroscopy.
Results and Discussion
The obtained series of five solutions each were sent for optical density studies at an electromagnetic wavelength of 515 nm. The direct measurement results are shown in Table 1 and Table 2 for excess iron and excess o-phenanthroline, respectively. Concentrations of each of the working solutions required for the subsequent plotting of the dependence and determining the straight line’s slope coefficients were calculated according to the Equation 7. The concentrations of the substance in the analyzed solutions with an excess of ligands were calculated according to the Equation 8.
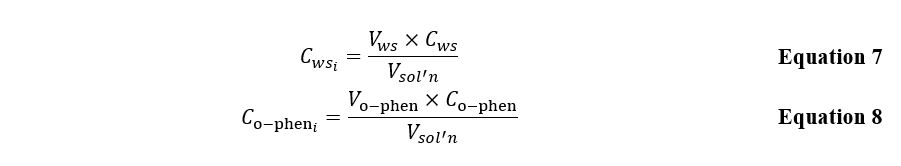
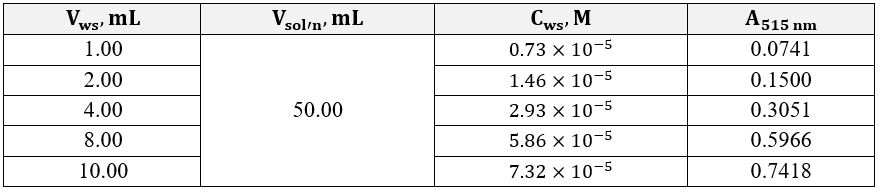
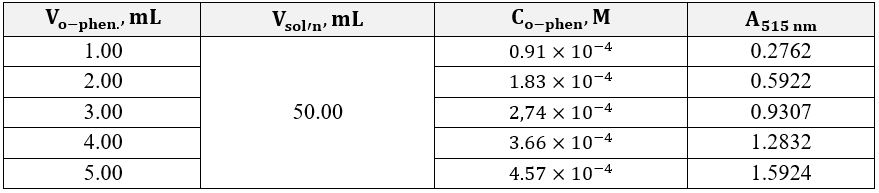
Figures 2 and 3 show the linear dependences of optical absorption on the starting substance’s concentration for iron and o-phenanthroline, respectively. Linear regression was used to determine the formula relationship and calculate the slope. The corresponding slope coefficients were 10,123 for the graph with excess iron and 3,635 for the graph with excess organic matter. Consequently, the ratio between the atoms in the complex can be calculated using Equation 9. It should then be shown that the complex formula based on the calculations is as shown in Equation 11. It is worth admitting that these data agree well with the known information where this complex is discussed as a correct version of the synthesis in the reaction sought 2,3.
Summary
To summarize, it should be noted that the spectroscopic method of investigation presents excellent opportunities for studying the formulation of complexes. In this work, the theory of Beer’s law and the relation of slope coefficients to the number of atoms in the inner sphere of the complex was used. For solutions with excesses of divalent iron, the slope coefficient calculated using linear regression was equal to 10,123, and for the series of solutions with o-phenanthroline, 3,635. The ratio of these numbers, equal to 3:1, showed the ratio between the components of the complex compound’s inner sphere, namely [FeII(o-phen)3]2+. The obtained formula of the substance agrees well with the data published in the literature. The relative error of the calculations was 7.33%. From this, it is possible to conclude that this work demonstrates a qualitative, meaningful study.
References
- Adhikamsetty, R.K.; Gollapalli, N.R; Jonnalagadda, S.B.; Complexation Kinetics of Fe2+ with 1, 10‐phenanthroline Forming Ferroin In Acidic Solutions. Int. J. Chem. Kinet. 2008 40(8), pp. 515-523.
- Budroni, M.A.; Calabrese, I.; Miele, Y.; Rustici, M.; Marchettini, N.; Rossi, F.; Control of Chemical Chaos through Medium Viscosity in a Batch Ferroin-Catalysed Belousov–Zhabotinsky Reaction. Phys. Chem. Chem. 2017 19(48), 32235-32241.
- Chouhan, S.; Kushawaha, A.; Jain, S.; Iron-Based 1, 10-Phenanthroline As ligands For Sensing Of Nitro Explosives. UGC CARE J. List G. I 2020 10(6), 133-139.
- Filimonova, T.A.; Volkov, D.S.; Proskurnin, M.A.; Pelivanov, I.M.; Optoacoustic Spectroscopy for Real-Time Monitoring of Strongly Light-Absorbing Solutions in Applications to Analytical Chemistry. Photoacoustics 2013 1(3-4), 54-61.