Introduction
The increasing emphasis on the question of the central problem of how long our lives last or how long a person can live continues to be investigated in econometrics. A study by Andrews shows the life expectancy (dependent variable) is affected by changes in the GDP of the country, income level, and other stochastic variables (12).
However, in this study, not all variables will be held ceteris paribus because of different factors such as uneven economic background and income levels of people. However, in this study, it was necessary to conduct an analysis by using the theoretical estimation of E ( y∨ w, c) because of the conditional effects of y on the two variables w, c hold.
In the expression, E( y|w, c) has a relationship with stochastic variables because it allows the model to accommodate other econometric variables other than those mentioned and used in the study. By using statistically available and recurring econometric panel data on health care, education, and others, econometric equations, it is easy to calculate the life expectancy of people easily (Greene 2).
Different economists have developed different models to answer the question of how long a person can live based on different variables. For instance, this study attempts to model the life expectancy of people on different variables to answer the fundamental question of “how can researchers use econometric factors to predict the lifespan of a person”?
Some of the models that have been developed are based on latent econometric variables that are based on policy. Greene argues that many of the answers are based on results from theoretical models, which show positive linear correlations that have been used to verify empirical data on the effects of econometric variables on the life expectancy of a person (3).
However, besides the economic variables noted above that dominate people’s life expectancy, other variables with the same effects include human capital investment, fertility, human behavior, human incentives, pensions, and intergenerational transfer accounts. Here, labor, which is a strong contributing factor to the GDP of a country in the form of human capital, makes a significant contribution to the well-being of people’s lives. Baltagi maintains that the empirical panel data on education and people’s health are some of the human capital factors, which are critical components that have serious implications on the life expectancy of people (4).
Human factors affect every aspect of the longevity of life and the economic performance of a nation. It is important to note that when people are healthy, they make significant contributions to the economic growth of a country. In conclusion, there is evidence to show that a positive causal relationship exists between the life expectancy of people and the economic growth of a country (Baltagi 4).
In this paper, life expectancy is represented by the dependent variable Y, which has a causal relationship with the independent variables, which include the Gross Domestic Product (GDP) of the target country (β1 = GDP), expenditure on education (EE), and expenditure on food (Food Expenditure) (FE). Typically, the model for econometric analysis is generally represented as:
Yi = β0 + β1 GDPi + β2EEi + β3PMVi + β4FEi + ε
The model was modified to make the next expression shown below.
GDPi (Xit – MXi) β + εit – Mεi+ MYi
Yit = β0 + β1 GDPi + β2EEi + β3PMVi + β4FEi + ε
Yit = (Xit – MXi) β + εit – Mεi+ MYi
The model is based on the assumption that there are stochastic variables besides those identified in the model that has an effect on the life expectancy of people in a country.
Research problem
The central problem of the life expectancy of a person has been modeled using different variables, leading to models that have some inherent weaknesses. The weaknesses have created a gap in knowledge to be filled in this paper by developing a comprehensive model by taking the life expectancy as the dependent variable and the GDP, education expenditure, average annual PM 2.5 value (2.5), and food expenditure as independent variables in a linear relationship using the following guiding objectives.
Study objectives
- Investigate the statistical relationship between the GDP of a country and the life expectancy of people
- To investigate the implications on the health of the people’s life expectancy
- Investigate the econometric effects of expenditure on education on the life expectancy of people.
- To determine how the average annual PM 2.5 value (2.5) (PMV) affects the life expectancy of people.
- To conduct an econometric analysis of the effects of food expenditure on the life expectancy of people.
- To combine the variables into a single life expectancy econometric model.
Research questions
- What is the econometric relationship between the GDP of a country and the life expectancy of people
- What are the implications of the health on the people’s on their life expectancy
- How does expenditure on education affect the life expectancy of people?
- How does the average annual PM 2.5 value (2.5) (PMV) affect the life expectancy of people?
- What are the effects of food expenditure on the life expectancy of people?
- What econometric model is obtained by combining the dependent and independent variables of the study?
Literature Review
GDP of a country and the life expectancy of people
The life expectancy and quality of life are affected at the national level because governments are obliged to use their resources to improve the quality of people’s lives (Baltagi 5). The quality of life can be determined by using different economic indices, which depend on the economic development of a country. A country’s Gross National Product (GNP) per capita and the Gross Domestic Product (GDP) per capita show the strength of the purchasing power, the parity of income, and the positive effects of the GDP and GNP on the life expectancy and quality of the people’s lives.
Typically, a wealthy country creates an environment for more people to earn more money, which they spend to improve the quality of their lives (Bergh and Nilsson 5). By using historical and present data, researchers can conduct an empirical inspection of the complex relationship between life expectancy and the GDP of a country (Wooldridge 2). However, the bulk of literature shows that most of the factors that affect the growth rate of the GDP of a country cannot be controlled.
Baltagi affirms that the best predictions of the growth rate of the GDP of a country can only be estimated using historical panel data (4). Here, the indicators of the quality of life include higher life expectancy, which is a community variable that is assigned the value of one, the material well-being of the people, job security, and political freedom, better family life with low rates of divorce, good climatic conditions, and gender equality (Baltagi 8).
The study showed in table1was conducted among 74 respondents using R as a multiple of 0.919, which was adjusted to R2 (0.823), having a standard error of 0.482. The results showed that some of the variables were positive, while others were negative. Here, political freedom gives -0.1052, job security, family life, and climate and geography scored negative values showing that the statistics with negative values indicate low-quality life.
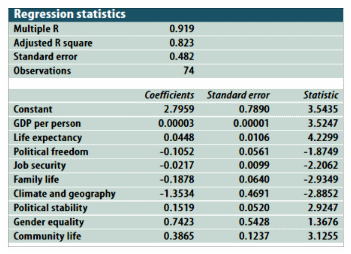
However, different models can be used to explain the relationship between GDP and life expectancy variables (Lancaste 5). The statistical approach provides a detailed study on the behavior of different variables and their effects on the relationship between the GDP and the life expectancy of a person. A study, which was conducted using the Generalized Additive Model to statistically analyze panel data by avoiding the ‘curse of dimensionality, showed that many of the variables used to make the model have a strong impact on the quality of people’s lives.
In addition, the model enabled the researcher to use non-parametric factors to conduct a non-linear regression analysis on the response variables. Here, the model exhibited the statistical components and properties of an asymptotic distribution with converging variables. Here, the general model can be expressed as:
Yi = β0 + β1Xi+ εi
The left side of the expressions shows the response variable, which in this case is the growth rate of GDP per capita for a designated country of interest. The model shows the exploratory variables that have a linear relationship with the growth rate of the GDP, which affects the life expectancy of the people.
On the other hand, the model can be modified to come up with a new model such that Yi = β0 + β1Xi+ εi where εi is the stochastic or error term, which shows the existence of heteroskedasticity. A clear restatement of the above-generalized model that includes life expectancy and the GDP is expressed below.
yij = ∑pj=1 fi (xjit) + μi + i
According to the expression, fi occurs as a univariate function that can be estimated from the expressions, and the variable xjit allows for an arbitrary correlation with the unobserved individual values of µi to occur. On the other hand, the errors that occur in the expression in the form of εi can be assumed to be independent of the effects of the distribution on the results of the study. However, the builders of the model argued that they could not place temporal restrictions on the variance of the results that were generated using the equations (Baltagi 23).
However, the model does not work well when unobserved effects that are caused by noise variables are still used in the equation. Differentiating the expression leads to the removal of the unobserved effects and a working solution.
yij – yit – 1 = ∑pj=1 fi (xjit) – ∑pj=1 fi (xjit – 1) + μit
Equation (2) above is obtained by subtracting the difference in the equations that result from lagging equation 1. By using the equations to estimate the interplay between the GDP per capita and the life expectancy, it is possible to model the two variables that represent the GDP and life expectancy of a person on a linear relationship (Lancaster 29).
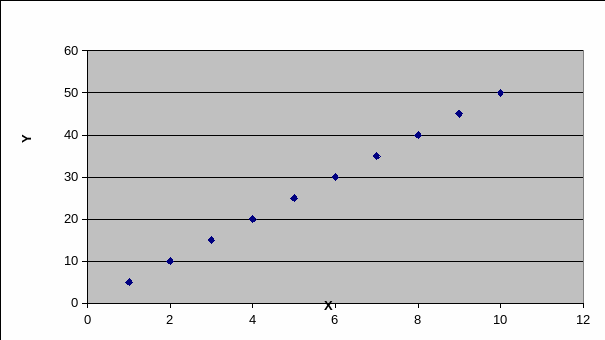
An investigation of the effects of the dependent and independent variables can be plotted on a regression analysis graph, which shows a strong positive correlation.
A study of the graph shows that life expectancy increases with an increase in the GDP of the country. The study shows that the linear model uses demographic factors and economic development as parametric variables to build the model. In this case, far more complex issues are factored when doing an econometric analysis of the effects of the GDP on the life expectancy of the people (MacKinnon and White 12).
One theory that has been used to explain the econometric relationship between the GDP of a country and the people’s life expectancy is the consumer problem. Here, the quality and utility of the life of a person depending on what they consume. In addition, issues such as positive wealth, the amount of wealth one has, progressive aging of a person, and the instantaneous probability of death can be used to form the equation shown below (Andrews 23).
Health and life expectancy
Research on the latent variables that have effects on the expectancy of life in the health care econometrics literature shows that the effects of consuming health care services and the money invested in health care two most important components that have critical effects on the quality of life and life expectancy (Mairesse 34). In addition, there is a reciprocal connection between the health of the people and the production function. A high production function denotes better income and high-quality life, which is one of the factors of the utility function.
Typically, health is seen as a capital investment in human beings because it leads to higher productivity based on Grossman’s model that shows the importance of utility in econometrics. The model enables an endogenous determination of the length of life, and the utility gained in the lifetime of a person (Mairesse 34).
Grossman proposed a health capital standard model for health care support, which states the investments in health care and the demand for health care services constitute the elements that influence the positive outcomes on the quality of people’s lives (2). According to Grossman, the relationship between health care expenditure and the quality of life translates to the life expectancy of people (9). Here, good health leads to a high production function and a longer life span. By making high capital investments in the people, the “timely and effective health care prevents the mortality of the people, leading to a longer lifespan” (Galı and Mark 1).
Galı and Mark conducted a study where they used life expectancy as a general indicator of health and the expected lifespan of the people (9). By using the per capita GDP on the health of the people as an independent variable, it was established that the people from countries with higher income levels lead better quality lives and have a longer lifespan than those who come from low GDP countries. Here, the health expenditure is high, and that could positively affect the lives of the people because the investment in health is higher.
The theoretical macroeconomic dynamic model based on regression analysis shows the relationship between life expectancy and health expenditure. The study used a hypothesis that was tested using multiple regression models with data from different countries. The test involved grouping countries with different GDPs, indicating the most developed and least developed countries. A correlation was done on the data using the following linear expression model.
LExp = 36.60 + 5.43 * ln (HealthExp)
The model shows a positive correlation between the life expectancy and health care expenditure of a nation by mapping the general equation Yi = β0 + β1Xi+ εi with into the following expression:
LExp = 36.60 + 5.43 * ln (HealthExp),
The coefficient, 0.543 of the health care expenditure, was an indicator of good microeconomic investment in the health of the people, which was counterproductive because for every unit invested, there was an equivalent output.
However, by introducing two variables into the model, it was possible to determine the points at which the lines of interception occur along the x and y axes when comparing the health expenditure of the two countries. The approach enabled the researcher to develop a linear model showing the points of intersection along the axes. Here, β is used to measure the elasticity of life expectancy using various factors such as the GDP of a country, health care expenditure, and investment in education.
Yi = β1 + β1X1i + β2X2i + β3X1i X2i+ εi
E (εi ) = 0
The above model is flexible because more variables such as poverty, pollution, and environmental issues could be accommodated in the model. On the other hand, by factoring the point at which the x axis is intercepted, the model could be manipulated into:
X2i=1:
E (Yi) = β1 + β1X1i + β2(1)+ β3X1i (1) = (β1 + β2) + (β1 + β3)X1i
X2i=0:
E (Yi) = β1 + β1X1i + β2(0)+ β3X1i (0) = β1 + β3X1i
The models show that health is a product good in which a country invests if it expects to increase the health stock of the people, greater healthy days, and an increase in wage levels. A study to determine the health expenditure and return on investment yielded an inverse relationship showing that when a person is born healthy or lives a healthy life, the medical expenditure on that person is low.
A similar study using 0.26 coefficient of elasticity on medical expenditure showed an increase of 2.6% increase in health when 10% increase in expenditure in health occurred. In conclusion, the higher the expenditure on medicine on a person, the higher the returns on investment and the better the quality of life of the person and the longer one expects to live.
Expenditure on education and life expectancy
Education plays an important role in shaping productive human capital in any country because it leads to economic development. It has been established that a country with high enrolment rates of students at the lower and higher levels of academic institutions is an indicator of the growth of the economy because educated people contribute positively to better economic growth. The effect is higher economic growth, better living conditions, availability of resources to invest in other sectors of the economy, and better quality of life that translates to longer life expectancy (Nelson 9).
The investment in education is an econometric variable that Keynesian economists used to evaluate the quality of life that governments offer to their citizens. Most of the microeconomic literature has analyzed the relationship between economic growth and investment in education by analyzing what the people earn and the quality of life their live.
A study of the behavior of the dependent and independent variables using an econometric model consisting of parameters that were determined by the use of Ordinary Least Square (OLS) in a regression equation was investigated. The researcher tried to minimize the errors that were caused by summing the squares to study the effects of education on the economic development of a country and the overall impact on the quality of life. Wooldridge conducted the study on the expenditure on education by modeling expenditure on the aggregate output function (10).
LnY = α + β1Ln (EDUEXP) + β2Ln (LFPR) + β3Ln (GFCF) + μi
The variables used in the equation include μi = error correction term, EDUEXP = Government Expenditure on Education % of GDP, GFCF = Gross Fixed Capital Formation, Ln = Natural Logarithm, Y = Real GDP, and LFPR = Labor Force Participation Rate. In this study, a time series data sample was used, covering the years between 1981 and 2010.
Table 1: Using the aggregate output function method.
The results show that the GDP has a 2.36 effect on the economic growth of the country if the y-intercept is at 2.36. However, the effect on economic growth that is caused by a GDP of 2.36 is achieved when the other variables are assigned a value of zero to temporarily remove their stochastic effects on the model. However, deducing from the model shows that if a government devotes part of its income to education, there is a positive effect on the GDP, which results in higher income. The model shows that a 1% change in the expenditure on education leads to 0.41% positive change in the GDP.
On the other hand, the study conducted by Wooldridge shows a very low coefficient of R2, which showed results that differed by 7.7% GDP leading to a right-skewed graph (21). When the graph is skewed to the right, the results do not validate the notion that spending on education increases the GDP and quality of life of the people.
Despite the above results being inconclusive, other studies to compare how the education factor influenced the life expectancy of people in East Java (Indonesia) was done. The study used a model used economic, social, health, and education and data from the central bureau of Central Bureau of Statistics of East Java using spline regression analysis (Bollerslev 19).
The results for all the 6 variables generated an F test statistic of 1, 0796 and a p-value less than 0.05, which showed the degree of freedom of the p-value. The results showed that education affected the quality of life and the life expectancy in Indonesia. Other factors that yielded significant values that were related to education include the number of years one attended school and an endogenous variable,
Determine how the average annual PM 2.5 value (2.5) (PMV)
The positive or negative outcome of the life expectancy of a person based on a study that used the co-variation of particulate matter with the people’s mortality rate when exposed to the particulate matters in the short or long term. In a nutshell, PM is a widespread air pollutant and any exposure to the particulate matters has serious consequences on the quality of life and the life expectancy of a person. However, the most commonly used indicators that describe the PM of matters are the “mass concentration of particles with a diameter of less than 10 μm (PM10) and of particles with a diameter of less than 2.5 μm (PM2.5)” (Popa 21).
In addition, ultrafine articles with a diameter of 0.1 μm or less can cause trans-boundary effects because they stay in the air for several weeks. The particles are said to have both anthropogenic and non-anthropogenic origins and chemical reactions. Exposure to the inhalable particles leads to high respiratory and cardiovascular morbidity and mortality from cancer, which causes repertory problems and high hospital admissions, which lead to higher expenditure on health (Galı, 12).
The short-term effects of respiratory infections show a 0.2–0.6% per10 μg/m3 of PM10 and long term effects of 6–13% per 10 μg/m3 of PM2.5.Here the short-term exposure to PM10 has a short-term effect on the health of the people, but PM2.5 has a stronger effect and more risks on the health of people, which increases the “cardiopulmonary mortality by 6–13% per 10 μg/m3 of PM2.5” when used on a person.
Determine how the average expenditure on food and life expectancy
It has been demonstrated in various studies that increasing the expenditure on food does not necessarily increase the life expectancy of a person. For instance, if there is a lot of farming going on and the people consume the food they grow, they will not be contributing anything to the GDP of the country showing that no linear relationship between the GDP per capita and the food produced exists because no exchange of money occurred (Popa 8).
A study of the expenditure on food and life expectancy can be described by analyzing household data and food expenditure against income. Heteroskedasticity occurs at the point where income and expenditure are depicted together because the way income was dispersed influences the level of expenditure on food (Greene 16). A linear model with Heteroskedasticity can be used to express the relationship between income and expenditure.
Income also has a heteroskedasticity effect on the quality of life assuming the ordinary least squares (OLS) are constant and unbiased. However, in this case, the standard errors are not taken to be biased to allow for the use of the usual statistical analysis tools such as the t-statistic. On the other hand, the analysis can be done even in the presence of OLS errors. By assuming that there is no loss of generality, the expression becomes:
Y = β0 + β1Xi+ εi
However, by assuming that there is heteroskedasticity, then, the equation has a high degree of consistency of the OLS, which is unbiased. The rationale is that E (ε|X) =0 and if X and Y are substituted in the equation, then the expression becomes E(Y |X) = β0 + β1X. In addition, the consistency property in the above equation has not been removed when considered under the heteroskedasticity. In addition, the variance of the error, which is expressed as var (εi) = α2 is not taken to be constant. The causes are that despite the people being under the same country with a high GDP, the expenditure on food varies significantly from one household to the other (Frey 7). The reason is that different families have different income levels and the number of family members is not constant. When related with life expectancy, again, other variable such as the health of a person, age, and the quality of medical care affect the life expectancy of a person. Typically, expenditure of money on food is one of the variables that affect the quality of life and the life expectancy of a person (Wooldridg 12).
Other variables on the life expectancy
While the above analysis has concentrated on education, health, GDP, food expenditure, and the PM 2.5 value (2.5) (PMV), it is fair to consider other variables to determine if they have an impact on the life expectancy of a person. An analysis done to determine the multi-collinearities with life expectancy used other variable such as Fertility Rate and Contraception Prevalence Rate, Country Development and Newspapers, CO2 Emissions and Commercial Energy U, school enrollments, and Population Growth and Urban Population Growth. The analysis showed a significant degree of correlation among the factors that influence the life expectancy of a person. For instance the ratio of the t-ratio for literacy rate when compared with the school enrollment was 1.30 and the t value was 2.20.
Methodology
Investigating the effects of various variables such as health, education, expenditure on food, GDP per capita, and many other variable on the life expectancy of a person depends on various indicators. A statistical analysis of panel data from different sources and theoretical models constitute the cohort of this study. The general model used in this study is a linear model that accommodates all variables in a linear relationship and appears as:
Yi= β0 + β1X1i + βnXni
The model will be analysed using time series and cross sectional panel data. However, panel data is always more biased towards cross sectional analysis because it depends on observations that are made over time. In this general model, Yit = Xitβ + Ziπ + εit (Yi = β0 + β1 GDPi + β2EEi + β3PMVi + β4FEi + ε), a regression analysis can be done on it because the heterogeneity effects are generated by constant terms in the regression model. However, the observed effects of heteroskedasticity do not uniformly apply in all cases, showing that there is lack of linearity in the behavior of the variables.
In addition, there is need to test for multicollinearity among the variables used in the model to determine the significance of the variables and their correlation with the life expectancy of a person. The variables of interest include the GDP, education, expenditure on food and education, and the PM 2.5 value (2.5) (PMV) and the life expectancy.
The data was analysed using a multiple regression analysis by fitting the variable into the equation, to create a linear model to solve the coefficients of the equation where the y-intercept occurs. On the other hand, a cross-sectional analysis of the life expectancy shows that it occurs at the point of data where the y-intercept occurs. However, to make the expression to accommodate a multiple regression analysis, there must be statistical significance among the variables.
Typically, among the requirements for a regression analysis is that the dependent and independent variables must be statistically dependent on each other to avoid the problem of multicollinearity. In addition, the study uses regression analysis to show that the data fits well into the model in this study because they are reflected in the t-statistic where t is used as the coefficient of determination for R2.
Results and Analysis
The results show that there are no effects caused by the presence of fixed variables on the dependent variable, which is the life expectancy. However, a correlation exists between the variables when the OLS estimators are used to show the biased nature of the independent variables such as the GDP, expenditure on education, and other variables that have already been discussed. In addition, the estimable equation of the model is embodied in all the observable effects of the group variables on the behavior of the model.
On the other hand, when the variables were formulated, they showed some heterogeneity, which do not have any correlation with the constant values. However, the model can be modified to show the random effects of the variables on the behavior of the model.
Yit = Xitβ + E [Ziπ] + + εit, which leads to = Xitβ + α + ui + εit
The above expression is an illustration of the random effects of the variables and their effects on life expectancy of the people. By manipulating the expression, it is possible to get a new expression whose behavior is affected by the random effects of the variables. However, suppose the constant term in the equation has observable effects on the equation using the differences across the units, the equation then becomes:
Yi = Xiβ + iαj + εi
However, the new equation has a linear relationship with other variables in a time T so that after the time elapses, a sample size of µT is obtained for analysis. If the unit vector is I in an expression, it is possible to collect different groups together in a given time, T to formulate the following model.
Y = Xβ + Dα + ε
A critical analysis of the model shows that it is a least squares dummy variable model that shows the relationship among the variables that affect the life expectancy of a person. The variables have a linear relationship with life expectancy as shown in the model, which consists of dummy variables for each group. However, it is not necessary to make the groups large otherwise there could be computational problems when analysing the data. In addition, it is possible to estimate the above model using the OLS because of the large number of dummy variables that are used in the equation.
The rationale for the dummy variables is that the additional effects are due to the noise variables that have been used in the model. However, it is important to make the model computationally possible by first determining the estimates of β by assuming that Mεi= 0. The rationale is that the group mean can be calculated using the expression MYi= MXiβ + α + Mεi. In the expression, the mean that was found after T observations were made is denoted by MYi because the equation or model was modified into a new form to accommodate the variables as follows.
Yit – MYi= (Xit – MXi) β + εit – Mεi
However, the use of α = MYi – MXiβ can be effected if the value of can be estimated in the equation. The value of α can be estimated by finding the difference between the means for each group and multiplying α with the mean values obtained from group X. The model becomes Yit – MYi= (Xit – MXi) β + εit – Mεi. However, the individual effects on the model are not yet explained and clarified.
Typically, the random effects of the variable are examined to see if they have any effect on the model. Here, the effects can be studied by finding the value of σ2ε, which is obtained by looking at the equation on the equation, Yit – MYi= (Xit – MXi) β + εit – Mεi and its relationship with the value of σ2ε.
To achieve that, the expression, Yit = Xitβ + α + ui + εit can be determined by use of the OLS squares because they are consistent and unbiased. The determinants from the regression can be used to determine the probability limit of the regression using the mentioned classical OLS, which becomes σ2ε + σ2u. However, by manipulating the expression, σ2ε + σ2u, it is possible to estimate the value of σ2ε.
On the other hand, if the number of parameters in the model is depicted by (K-1), the model shows a significant occurrence of heteroskedasticity that is spread across the variables used to build the model. In addition, it is evident that the model performs well across all the variables used in the study because the model, Yit – MYi= (Xit – MXi) β + εit – Mεi, shows that each variable has a significant impact on the life expectancy of the people. In other words, the life expectancy of the people depends on the variables mentioned and used in the study, with each variable having a significant impact on the life expectancy of the people.
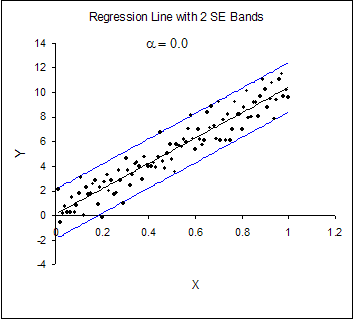
It is clear from figure 1 that the y intercept when the value of alpha is equal to 0 is at 0.2 on the x axis and -2 on the y axis. On the other hand, when the value of alpha is changed to 0.2, the x intercept occurs at zero and they intercept occurs at zero also.
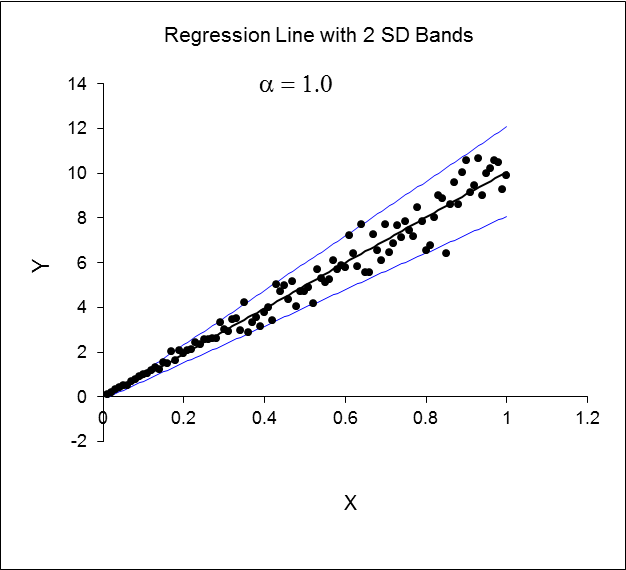
It is important here to note that the rule of thumb was followed because of the presence of heteroskedasticity when analyzing the data, which has some effects on the OLS estimates in the equation. The rule of thumb was used to ensure that the coefficients in the estimates were not biased even if they were inefficient in determining the impact of the variables on the life expectancy of the people. On the other hand, the dispersion of the OLS was kept as close as possible to increase the accuracy of the model and reduce the errors to which the model was prone to.
On the other hand, the σ2 was used to investigate the potential impact and behavior of the variables because σ2 can be a multiplier in the model. In conclusion, it is possible to say from the analysis that many more variables affect the life expectancy of a person, besides the variables mentioned and used to model the relationship between life expectancy in the left hand side and independent variables in the right hand side.
However, to be sure that the effects of multicollinearity on the model are removed, the dummy variables, which are many in the study are catered for by defined at the start of the process of formulating the model. By defining the variables correctly, it is possible to avoid perfect multicollinearity so that any errors that happen during the regression analysis can be detected when computing the data.
In conclusion, the model shows a strong relationship between the life expectancy of people with the independent variables such as expenditure on food, the GDP of the country, the level of education of the people. However, it is clear from the study that other variables not mentioned in the study have additional effects on the life expectancy of a person such as the quality of medical care, which form part of the group variables that introduce the problems of heteroskedasticity and multicollinearity, which can be avoided to make the model as accurate as possible by making the dispersions of the OLS as close as possible.
Works Cited
Andrews, Donald WK. “Heteroskedasticity and autocorrelation consistent covariance matrix estimation.” Econometrica: Journal of the Econometric Society (1991): 817-858. Print.
Baltagi, Badi. Econometric analysis of panel data. Vol. 1. John Wiley & Sons, 2008.
Bergh, Andreas, and Therese Nilsson. “Good for living? On the relationship between globalization and life expectancy.” World Development 38.9 (2010): 1191-1203.
Bollerslev, Tim. “Generalized autoregressive conditional heteroskedasticity.” Journal of econometrics 31.3 (1986): 307-327.print.
Galı, Jordi, and Mark Gertler. “Inflation dynamics: A structural econometric analysis.” Journal of monetary Economics 44.2 (1999): 195-222.Print.
Greene, William H. “Solutions Manual Econometric Analysis.” (2000). Print.
Frey, Bruno S., and Alois Stutzer. Happiness and economics: How the economy and institutions affect human well-being. Princeton University Press, 2010. Print.
Lancaster, Tony. The econometric analysis of transition data. No. 17. Cambridge university press, 1992.Print.
MacKinnon, James G., and Halbert White. “Some heteroskedasticity-consistent covariance matrix estimators with improved finite sample properties.” Journal of Econometrics 29.3 (1985): 305-325.Print.
Mairesse, Jacques, and Pierre Mohnen. “Using innovation surveys for econometric analysis.” Handbook of the Economics of Innovation 2 (2010): 1129-1155. Print.
Nelson, Daniel B. “Conditional heteroskedasticity in asset returns: A new approach.” Econometrica: Journal of the Econometric Society (1991): 347-370.Print.
Popa, Ana-Maria. “The Impact of Social Factors on Economic Growth: Empirical Evidence for Romania and European Union Countries.” Romanian Journal of Fiscal Policy (RJFP) 3.2 (2012): 1-16. Print.
Wooldridge, Jeffrey M. Econometric analysis of cross section and panel data. MIT press, 2010. Print.