Maths Information: Inverses of Functions Essay

Introduction

A function is called one-to-one if no two values of x produce the same y (Dawkins, 2007 p.198). This can be demonstrated best using an example of a function that is not one-to-one. Example, the function f(x)=x² is not one-to-one because both f(-2)=4 and f(2)=4. Geometrically, the graph of f(x) would then be intersected twice by the horizontal x-axis line at the points 2 and -2. But the function can be made one-to-one if it’s restricted to 0≤×≤∞. Therefore it’s important to note that only one-to-one functions can be inverse functions. In other words, a function is one-to-one if and only if no horizontal line intersects its graph more than once. Example, a function f(x)=x³, and x₁ ≠ x₂ then x³₁ ≠ x³₂ therefore two different numbers can’t have similar cube, by above definition, then f(x)=x³ is one-to-one.

Given two one-to-one functions f(x) and g(x), if (fog)(x)=x and (gof)(x)=x, then we say that f(x) and g(x) are inverses of each other (Dawkins, 2007 p.198). Therefore, we can say that

g(x) is the inverse of f(x) and denoted by g(x)=f¹(x) and f(x) is the inverse of g(x) denoted by f(x)=g^-1(x). Caution should however be made at this point not to confuse f¹ for an exponent. Thus, f¹(x) does not mean 1/f(x). The reciprocal of 1/f(x) can however be written as [f(x)]^-1.

Steps of finding the Inverse of a Function

Below are steps to finding the Inverse of a Function.

1. The first step will involve replacing f(x) with y. This is done to make the process easier.
2. Then, replace every х with a y and every y with an х.
3. Solve the equation from step 2.
4. y is then replaced with f¹(x). At this stage we have found the inverse.
5. At this stage we verify our work by checking that (fof^-1)(x) and (f¿¿ -1 of)(x)=x¿ are both true.

Example of an inverse function

Example 1

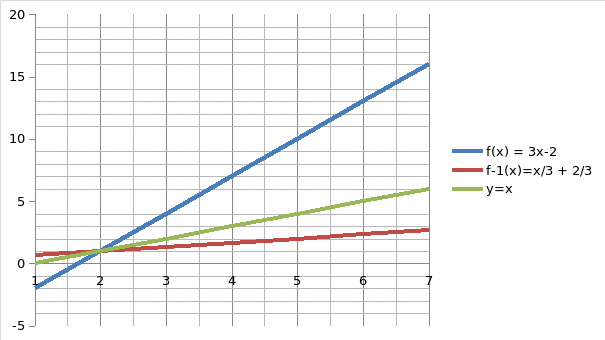
Given f(x)=3x-2 find f¹(x).

Solution

The first step is to replace f(x) with y. Therefore, y=3x-2.

In the second step we will replace all х with y and all y with х.

Therefore, х = 3y-2_x.

Solving for y, x+2 = 3y → 1/3(x+2) = y → x/3+2/3 = y

Then finally we replace y with f^-1(x) → f^-1(x) = x/3+2/3 which is the inverse of our function above

Verifying the results that (fof^-1)(x)=x

Example 2

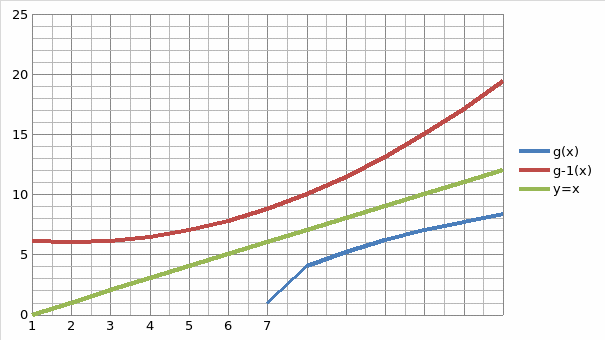
Given the function g (x) = 1+3√x-6

find g^-1(x)

Solution

The first step is to replace g(x) with y. Therefore

y=1+3√x-6

Secondly, we replace all x with y and all y with x.

Therefore

x=1+3√y-6

Solving for y

Finally, replacing y with

Verifying the result that (gog^-1)(x)=x

The graph of the function and its inverse

Below are graphs of the functions solved above and their inverse. It can be seen that the inverse is a reflection of the actual function about the line y=x.

Conclusion

For a function to have an inverse it must be a one-to-one function. This can be tested using the horizontal line test that no horizontal line intersects the graph more than once, and manually, by checking that the function never takes the same value twice f(x₁) ≠ f(x₂) whenever x₁ ≠ x₂.

References

Dawkins, Paul. (2007). Paul’s Online Math Notes. College Algebra (Math 1314). Web.