Introduction
Cyclotrons are technologies used to accelerate charged ions in a vacuum lying between two magnets with a strong magnetic field. The particles injected into the systems are either from internal or external sources. Each of the sources has specific benefits based on the functionality and behavior of the ionized particles. Typically, the particles move in circular orbits with the centripetal force acting on them mathematically modeled based on either relativistic or non-relativistic environments. Typically, in a relativistic environment, the ionized particles acquire centripetal forces due to the effects of the transverse magnetic field. The field, B goes through an angular displacement, w, mathematically expressed as Bqv. On the other hand, cyclotrons are designed to generate uninterrupted stream of a beam ionized particles. However, some limiting factors are related to the relativistic detuning and the behavior of the radial magnetic field. Therefore, ideal situations cannot be attained in the process. Large areas of magnetic fields are applied in restricting the moving ions during their translation from zero energy to new energy levels which are acquired at the output. As mentioned above a number of cyclotron machines have been designed for the specific purpose of accelerating charged particles. Some examples are discussed in the following document which details the mathematics of cyclotrons and the behavior of ions that form the main focus of the study.
Literature Review
Cyclotrons are systems designed and developed for the purpose of accelerating hydrogen ions in a magnetized environment. The accelerated particles acquire characteristic properties specific to the energy of the accelerating environment. These particles move in a circular path since the magnetic field is circular in nature. The circular motion creates a centripetal that acts on the moving particles (Su, Wagner & Grobe, 3). In order for the particles to move in a circular path, the particle accelerator has a vertical magnetic field that alters the trajectory of the particles into isolated cavities. Analytically, the particles may not always move in circular orbits and that depends on the architecture of the cyclotron. Large cyclotrons are made of different sections that are either circular or straight in nature, depending on the position of the accelerating component (Kim, Kwon & Lee, 2).
Different types of cyclotrons have been developed with different characteristics and capabilities. One characteristic common to all cyclotrons is that they can accommodate charged particles from internal and external sources (Kim, Kwon & Lee, 3).
Typically, some of the machines have been designed and developed to propel negative hydrogen ions (H–). The movement of the H– ions in an energized field is referred to as cyclotron motion (Kim, Kwon & Lee, 4).
Some of the cyclotrons are circular in their design. Circular machines are characterized by particles which repeatedly orbit through the same path with each event registered in the same acceleration gap. Notably, a low gap voltage is an important prerequisite to the acquisition of higher kinetic energy levels (Kim, Kwon and Lee, 5).
Different energy machines have been designed with significant functional advantages while previous machines only have historical significance.
The study is going to focus on circular machines. In that respect, there are various circular cyclotron machines in use today. Typically, cyclotrons are designed to generate an uninterrupted stream of particles. These particles are subjected to large areas of magnetic fields applied to restrict ion movements during their transition states from zero energy levels to higher output energy levels. As mentioned above a number of cyclotron machines have been designed for the specific purpose of accelerating charged particles. These cyclotrons operate on different principles as discussed below (Kim, Kwon and Lee, 6). It is important to mention some of the cyclotrons at this point.
- Uniform field cyclotron
- Separated sector cyclotron
- Azimuthally-varying field cyclotron
- Superconducting cyclotron
- Spiral cyclotron
The uniform field cyclotron was the first to be designed and developed for scientific use during at the onset of the technology. Thus, the cyclotron has a lot of historical significance in the scientific discipline. Each of the cyclotrons is has characteristics. One such is the separate sector cyclotron. The cyclotron is characterized by several separate sectors that bend the magnetizing force into a number of sectors. The cyclotron operates on the principle of molarity. The modularization technique is used to construct the constituent magnets to equip them with the capacity to apply accelerating forces on the rf feeds that lie between the sectors (Su, Wagner & Grobe, 3)
On the other hand, the spiral cyclotron operates on the principle which recognizes the spiral boundaries which have a pole positioned at the center of the spiral. The high field regions at the boundaries of the cyclotron enable the moving ions to be inclined while in motion. On the other hand, a vertical confinement of the moving ions can be achieved by using an edge focusing mechanism. To further increase the vertical confinement of the ions, two techniques are used. These include the focusing and defocusing techniques (Su, Wagner & Grobe, 4).
Different cyclotrons utilize different techniques to focus ions. Superconducting cyclotrons utilize to a significant extent the focusing technique. Ions in the cyclotron which utilize the technique are characterized by a high degree of compactness which is a desirable characteristic for cyclotrons. Additionally, the predictability of the electric field of the cyclotron can be made more accurate (Su, Wagner & Grobe, 5).
Focus Mechanisms
Characteristically, early cyclotrons used a weak focusing mechanism and operated in a field index typically defined by n<1. The stream of the resulting beam occupied a large area. On the other hand, modern cyclotrons have a focusing mechanism that relies on lenses that exploit the technique of transverse focusing systems. However, it is of critical importance for the magnets to be precisely positioned, thus reducing the size of the occupied space (Su, Wagner & Grobe, 5).
These machines operate on different principles as examined below.
Uniform Field Cyclotron
The kinetic energy acquired by the accelerated particles and the gryofrequency of the non-relativistic ion forms the basic operating principle of the uniform field cyclotron. The kinetic energy of the moving ion places it in an orbital motion creating a field that is orbital in nature constraining the ions into an orbital path. The figure below illustrates the behavior of the entire machine in constraining ions to a circular path with the acting magnetic force remaining perpendicular to the moving electron. In the following illustration, ions are accelerated in a field with a D shaped metal structure. The structure is positioned within the field region. Typically, the entire system becomes operational by applying an electric current from the rf resonator. The functionality of the resonator can be optimized based on the mathematical relation wg (Su, Wagner & Grobe, 6).
The path of the accelerated particle is illustrated in the diagram 15.1b below. The principles upon which it operates is based on low energy ions which experience an accelerating force towards the positively charged environment which constitutes half of the rf cycle. The ions move through a gap containing an electric field which may distort their movement. However, during the return cycle, they are shielded from the effects of the electric field to force them move in a circular orbit. On their return path, further energy is applied on the ions to accelerate them further to boost their energy. Typically, that is achieved by reversing the polarity of the dee (Su, Wagner & Grobe, 7)
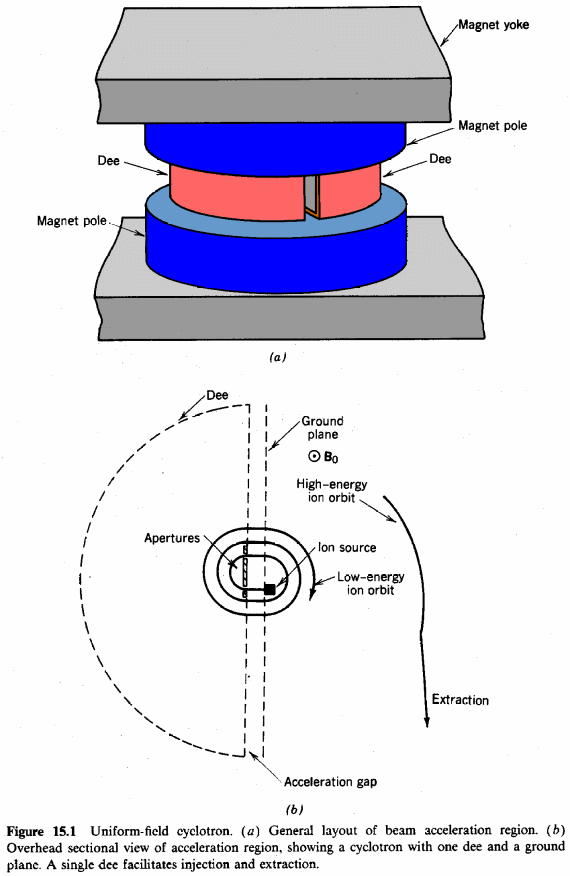
The entrance into the acceleration gap consists of an aperture that limits the range of the ions. Typically, a limiting factor is incorporated into the design of the machine to reduce the energy spread of the ions. Then the ions are accelerated through the gyro-radius to boost their kinetic energy before they are eventually extracted. Mathematically, gryofrequency is related as illustrated below.
Fo = qBo/2µmi= (1.52×107) Bo (tesla)/A.
In the mathematical expression, A is the atomic mass number of the particle under consideration. Observations indicate that the frequency of the system in question is in the range of 10MHz. The frequency has been observed to lie in the range of 1 Tesla. On the other hand, the energy acquired by the accelerated ion is subject to limiting factors. The limiting factors include relativistic de-tuning and the intensity of the radial magnetic field. Therefore, ideal situations cannot be attained in the process (Su, Wagner & Grobe, 8). However, the variables that influence the outcome of the ions are expressed mathematically as follows.
Tmax= 48 (Z _RB) 2/A
Typically, the mathematical relation is specifically applied on a uniform field magnetic environment. However, the above relation provides a mathematical expression of the kinetic energy acquired by the moving ion. In addition to that, other variables such as the non-relativistic orbital radius of the stream under examination can also be calculated. The units of measurement for the variables used in the mathematical relation include Tmax measured in MeV, R measured in meters, and B which is measured in Tesla.
On the other hand, transverse focusing is performed on a small field which is azimuthally symmetrical. In addition to that, the operation occurs in a radial field with the orbits covering a wide range of radii. That is because magnetic fields are positioned vertically. The radial variations are influenced by the magnetic fields and the magnitude of the field index has no direct or inverse relationship with the magnetic radius. Mathematically, the field index should be maintained at a zero value at the center of the magnetizing force (Vorobiev &York, 6).
The value of the field index, n, has to be designed to meet the above mentioned requirement to fit into the magnetizing environment of the cyclotrons. An appropriate value of n provides a case to minimize the value of the orbiting particles with a desynchronization property. The following diagram illustrates the whole concept of the magnetic field which is descriptive of a uniform field cyclotron.
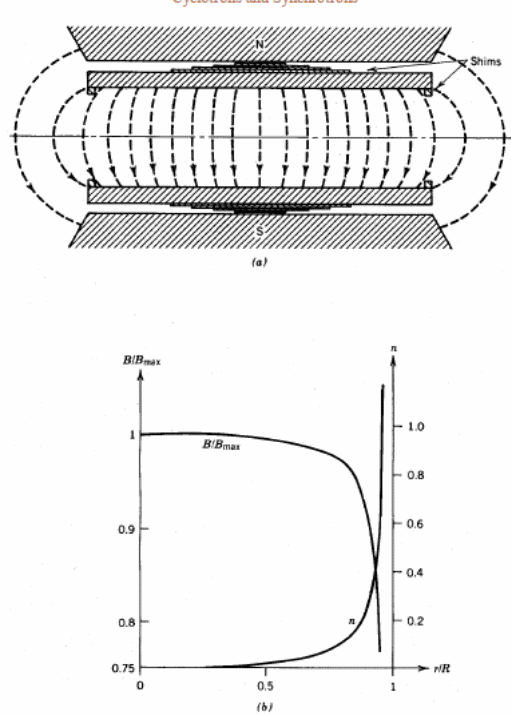
The diagram above indicates the behavior of magnetizing shims which define the optimal distributions of the magnetic field. On the other hand, diagram b illustrates the behavior of the vertical field magnitude.
Typically, low energy ions are acquired by focusing them electrostatically. On the other hand, the field patterns differ significantly by providing the service of the immersion lens that is typical of a single dimensional equivalent of electrostatic forces. During the particle acceleration lifecycle, a level of particle energy and speed may be acquired by focusing the ions towards the entrance of the exit while deflecting them from the exit.
Typically, when the particles are in motion, they exhibit specific characteristics as they revolve within that system by acquiring higher levels of energy when in motion. It is important to note that the lifecycle of the ions have to be noted or documented using software tools that have been designed for the purpose. It is important to identify tested and proved tools when selecting a software tool for the purpose.
Ion extraction
Eventually, ions can be extracted from the machine by applying a deflection mechanism on the ions. Typically, the deflection allows ions to be extracted at any point in the machine. In order to ensure the ions are captured effectively, ions with the maximum amount of energy are deflected (Vorobiev &York, 3).
The captured ions have to be shielded from the effects of the electric and magnetic fields using a mechanism that allows a separator or a septum working in tandem with an electrode with an image charge current to shield the ions from the effects of the electric and magnetic fields.
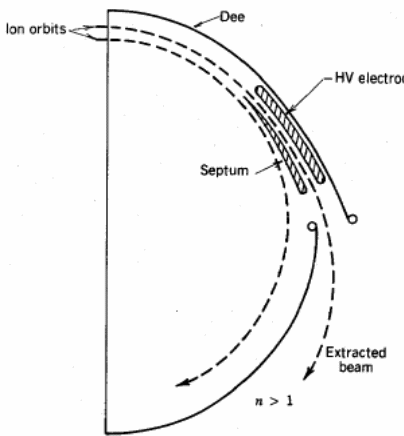
Separator
To attain the maximum deflection of the ions, a strong magnetic and electric field is applied on the ions to deflect those ions with maximum energy. Typically, the radius of deflection is characterized by the relation, n>1. The trajectories of the electrons have to be well established and defined. Observations indicate that the ions move in a spiral manner when subjected to the deflecting fields as they move out of the separator. It is important to harvest an optimal number of ions during the deflection process by designing the cyclotron to minimize the number of interruptions on the ions. However, it is not in the scope of this study to evaluate the design criteria for capturing the ions based on the design of any cyclotron (Vorobiev &York, 4).
Observations based on the orbits of streaming particles indicate that they occur in large orbits and the separation can be calculated based on the mathematical relation shown below:
R =(R/2) (2qVo sin Ɵ s/T).
Typical Examples of Cyclotrons
Many technologies have been developed to demonstrate how cyclotrons work. A typical example of a cyclotron that may acts as a learning point on a practical basis is the BEST 35 CYCLOTRON. Typically, the cyclotron is designed to accommodate negative hydrogen ions only (H–). It is also designed to operate with an extraction beam voltage which is between 15 and 32 MeV.
A number of characteristics inherently define the characteristics of the machine. These include the main magnet which is part of the machine. Typically the architecture of the main magnet enables it to accommodate a four sector coil current with a capacity equivalent to 9800AT. On the other hand, rf resonators constitute a connective frequency of 70Hz with a dee voltage equivalent to 50Kv. In addition to that, the machine oscillates with an oscillatory harmonic equivalent to 4. One characteristic of the ion source is that the ions are externally injected with an injection line that operates with a current in excess of 15 mA. Technically, the particles move in a spiral path to the axial injector.
On the other hand, a vacuum acts as the source of the ions that are extracted using a simultaneous dual beam with beam lines following a 2 way and 3 way switching magnet.
Another type of cyclotron in commercial use is the BEST 14 CYCLOTRON. Typically, the cyclotron is designed to operate at a 14MeV capacity. It operates on a fixed energy multi-foil carousel. The cyclotron operates by integrating internal and external sources of ions. One additional benefit or characteristic of the machine is that it can be upgraded to accommodate ions from different sources depending on the nature of the environment under consideration. The flexibility of the machine is based on projections which increase in strengths based on the dunes and the energy of the beam.
One general characteristic of the system is its control system. The control system is characterized by a real time mechanism that allows users to control the functionality of the machine and to allow real time communication of safety signals. Typically, the system is computerized and input and outputs are communicated through a computerized system. A software mechanism provides a link to the system and provides a reliable interface between the system and the user. Cyclotrons play different roles in different industries. One such industry is the hadron therapy.
Cyclotron for Hadron Therapy
A real life experience where cyclotrons are used is in the medical industry. One such is in the hadron therapy. The cyclotron has various characteristics. Some of the typical characteristics include its ability to deliver a range of particles that allows it to be tagged as one of its kind in the world today. Typically, particles delivered by the cyclotron include alpha particles, carbon particles, and protons. An electrostatic generator plays a critical role in the extraction of the particles mentioned above (Sabaiduc, Du, Boiesan, Zhu, Suthanthiran, Johnson, Ladysmith, Gelbart & Conard, 4).
It is important to note that the particles accelerated include carbon and helium ions which are subjected to a 400MeV/u. On the other hand, hydrogen ions are projected to be accelerated by a 265 MeV/u which are purposely extracted using a stripping mechanism.
The magnetic core of the cyclotron is 6.6 m in diameter with the entire mass of the magnetic core being 700t. On the other hand, superconducting coils are integrated into the design by enclosing them into the cryostat (Sabaiduc, Du, Boiesan, Zhu, Suthanthiran, Johnson, Ladysmith, Gelbart & Conard, 3).
The basic operating concepts are based on different parameters. These include a fixed amount of kinetic energy, a constantly applied magnetic field, and an integrated rf frequency mechanism that allows switching between different streams of accelerated ions (Sabaiduc, Du, Boiesan, Zhu, Suthanthiran, Johnson, Ladysmith, Gelbart & Conard, 3).
The Magnetic System
The magnetic system of the entire component structure consists of symmetrically arranged spiral sectors. In addition to that, the magnetic mechanism borrows from the deep-valley concept that incorporates elliptically shaped pole gaps. Typically, the design of the magnetic system optimally utilizes the space reserved for the magnets integrated into the system. Low levels of resonance, ability to attain a vertical tune equivalent to a Qz value of 0.4 specifically targeting areas from which the ions are extracted, and the ability to maintain the last orbit of the stream of ions close to working and acceptable levels are some of the benefits derived from the system. In addition to that, the entire system incorporates a strong acceleration system (Vorobiev &York, 4).
Acceleration System
The main function of the acceleration system is to enable the ions acquire an orbital frequency equivalent to 75MHz making in order to acquire a threshold of the 4th harmonic level. Typically, the functionality of the system is based on a pair of conducting cavities positioned opposite one another in the operating valley of the component. On the other hand, the dee is 20 mm thick with rounded edges that are 10 mm thick with blunted or circular finishes (Kim, Kwon and Lee, 2).
Ion Dynamics
The dynamics of the ions involved in the study can either be in closed orbits or open orbits. Typically, the ions resonate with different radii within acceptable parameters. Typical examples of values generated from the environment are tabulated below.
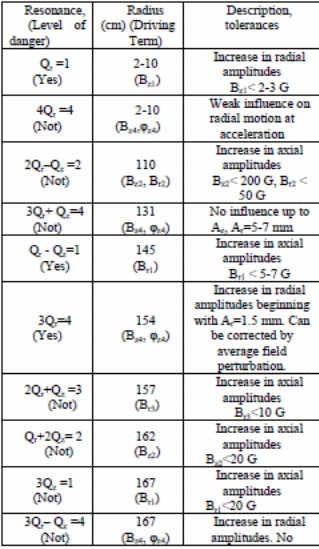
On the other hand, the system has to conform to vacuum requirements specific to the operational functionality of the machine (Kim, Kwon and Lee, 7). Typically, the following section details vacuum requirements for the set up.
Vacuum Requirements
The efficiency of the cyclotron can be hampered by the residual gas molecules which reduce the strength of the streaming ions due to bombardments between the ions and gaseous molecules in the system. That weakens the intensity of the beam which has a strong correlation with pressure variations in the in the cyclotron (Sabaiduc, Du, Boiesan, Zhu, Suthanthiran, Johnson, Ladysmith, Gelbart & Conard, 5).
One most important benefit of the system is that it is projected to provide a beam of protons that can be used in MeV/amu machines which can be attained using a compact environment (Kim, Kwon and Lee, 4).
Radiation Shielding
Radiation is one of the critical factors to consider in the design and installation of a cyclotron. Large cyclotrons are susceptible to emitting large amounts of radiation and should be considered in the design. Typically, cyclotrons should be installed in a thick walled environment inside a bunker. Typically, the installation and shielding of the cyclotrons differ significantly with each other. Smaller cyclotrons are configured to be accommodated in lighter radiation shields (Sabaiduc, Du, Boiesan, Zhu, Suthanthiran, Johnson, Ladysmith, Gelbart & Conard, 3).
It is important in the study to examine methods used to attain high level of focused ions in cyclotron systems (Vorobiev &York, 3).
Principle of Operation of Cyclotrons
Typically, cyclotrons operate by energizing particles which are then accelerated in a spiral path through a space which exists between two dee cylinders enclosed in a vacuum chamber. Notably, an equipotential condition defines the volume between the dee and the enclosing chamber. In addition to that, to achieve the desired acceleration potential for the ions, the volume of the dee is designed to lie between two magnetized poles to enable the magnetic field act on the ions effectively. The design restricts the ion movements to a circular and flat path. The potential difference experienced in the dee enables the ions to acquire higher acceleration speeds in their path (Sabaiduc, Du, Boiesan, Zhu, Suthanthiran, Johnson, Ladysmith, Gelbart & Conard, 6)
Identifiably, the beam particles originate from the center of the cyclotron iteratively acquiring more energy as the ions keep moving through the same path.
The projectiles of the accelerated particles enable the particles to gain more energy with each pass as the radius of the projectile increases. The path length of the ionized particle is related to the energy of the particle in the following mathematical equation.
Ekin= (q^2r^2B^2)/2m.
Each of the above variables is related to the other variables in the equation and represents different factors. Thus, r symbolizes the radius of the stream of ions under projection. On the other hand B and Ekin represent the strength of the magnetic field. To successfully operate the system, a compensatory scheme is used where the increase in the velocity of the particles in relation to the path of the stream of ions is integrated into the system. In addition to that, the ions under acceleration have to acquire a positive charge at the time they cross through the path to enable the particles accelerate further. Typically, all the operations therefore rely on the principal of phase stability (Vorobiev &York, 4).The above status can be calculated based on the using the following mathematical relation.
V=qB/2m and v=v/2m
The particle velocity is represented in the relation by v. The particle streams move on a radius defined as r in the equation. It is important to note that an increase in the relativistic mass is directly related to an increase in the energy of the streaming ions (Vorobiev &York, 3).
Methodology
The study provides a general inquiry on cyclotrons both in practice and in theory. A literature review in particular has focused on technical details about the uniform field cyclotron and further studies on the behavior of the ions and approaches used to capture moving ions are detailed. A theoretical framework for studying the behavior of ions in motion is based on an experimental set up detailed below. A literature review and a detailed examination of the behavior of the particles will inform the study.
Having studied the mechanism of the cyclotron, it is important to examine the theory of cyclotron motion as an experimental set up.
Suppose two different environments in the above mentioned cyclotron are set up and considered in the study. The environments under examination include a circular polarized field and a linear polarized field. Suppose the behavior of a particle of mass m is examined which has a charge q. Assume the magnetic field under which the particle is moving is uniform and defined by the relation B = B0^ez. Suppose the electric field is defined by E which is a time influenced value and suppose the electric field is orthogonal and defined by B. Analytically, different variables will be obtained from the setup. These variables include vector ^ei, which acts along the direction i. An experimental analysis of the motion of the particles is analyzed later in the study. In the setup, one force is allowed to exit along the z direction while the motion of the particle takes place in the xy plane.
Circular Electric Field
The circular electric field can mathematically be related in the following expression that allows us to determine the level of polarization of the circular electric field (Kim, Kwon & Lee, 2).
E = E0 cos wt ^ex + E0 sinwt ^ey
Typically, there are two potential issues to consider in the relation. One of the potential factors to consider in the relation is the scalar potential. The other factor is the vector potential. Both potentials can be presented mathematically by the mathematical symbols α, and A respectively and expressed below.
α =xE0 coswt – yE0 sinwt;
On the other hand, A is represented mathematically below.
A=yB/2 ex×+xB/2ey
Typically, we consider in this relation a non-relativistic motion, two constants of motion result from the equation. On the other hand, a relativistic motion may also result in specific constants under consideration. Therefore, both types of motions are integral in nature while the electric field indicates a polarization that is characteristically circular in nature (Venturini, Kishek&.Reiser, 3).
Linear Polarization
On the other hand linear polarization can be mathematically expressed based on the stream polarization direction. Typically, the mathematical presentation of the electric fields is illustrated below (Kim, Kwon & Lee, 4).
E = E0 coswt ^ey:
In this case, the scalar potential subject to use is illustrated above. On the other hand, the vector potential is similar to the equation, A=yB/2 ex×+xB/2ey
is mentioned above.
On the other hand, the rotating frame can be evaluated based on the following equation:
L=1/2m(x^ 2 + y^2) -1/2m(x^2 + y^2)µ^2+qE0(y cost coswt-x µsint coswt).
Results
It can be concluded from the above mathematical results that the movement of a particle that has been ionized in a magnetic field is characteristically defined as an integral of a circularly polarized field. Typically, the above findings apply to a relativistic environment for the moving particle. On the other hand a non-relativistic movement of particles has no correlation with the charge on a polarized environment and is an integral function irrespective of the environment under consideration. The environment may constitute circularly polarized fields or linearly polarized fields depending on the choice taken. In addition to that, the nature of the motion defined by a relativistic environment is qualitative in nature and is strongly correlated to the polarization state of the field under which the study is being conducted. Typically, a rotating frame provides clearer insight into the effects of a polarization on a moving ion. On the other hand, the rotating stream is proven to be strongly influenced by the magnetic field and the degree of polarization of the magnetizing environment (Kim, Kwon & Lee, 3).
Discussion
Cyclotrons are a historical development that has gone through different development phases with a lot of scientific significance. Typically, a stream of particles is accelerated through a circular or closed orbit. The trajectory of the particles can be reflected by applying a force on the trajectory due to a magnetic field on the stream of ionized particles. Typically, these particles can be re-circulated to achieve higher levels of resonance while in orbit. As the particles continue passing through the same field repeatedly, ions acquire higher levels of energy and speed.
Different types of cyclotrons are characterized by different operational functionalities. One of the earlier cyclotron inventions was the uniform field cyclotron. Typically, the machine could work on a 15MeV capacity. The operational efficiency of the machine depends on the increase or decrease of the relativistic mass of the ionized particles. On the other hand, a number of cyclotrons have been developed and their operational efficiency examined depending on the strength of the magnetic field and other design factors. Typically, the ions keep moving and acquiring higher resonant capabilities based on the phases covered by the particles as detailed by(Sabaiduc, Du, Boiesan, Zhu, Suthanthiran, Johnson, Ladysmith, Gelbart & Conard, 3).
Two examples of the operating environment include a circular field and a linear polarized field. The relativistic motion of a moving charged particle is characterized by influencing factors that are inherently defined in the relation. Typically, the entire environment is integrative, be it polarized or not. On the other hand, the entire working environment is not integrative if the functional environment is non-relativistic. On the other hand, different approaches are used in viewing the particle behavior in either a relativistic or non-relativistic environment.
Either is mathematically related based on the variables of the operating environment. The mathematical relations are illustrated below as detailed by (Sabaiduc, Du, Boiesan, Zhu, Suthanthiran, Johnson, Ladysmith, Gelbart & Conard, 4).
For linear polarization, the electric field is mathematically related as follows:
E = E0 coswt ^ey:
On the other hand, for a circular electric field the mathematical relation is provided as follows:
E = E0 cos wt ^ex + E0 sinwt ^ey
Typical examples of cyclotrons include the 400MeV Hadron therapy machine that is applied in the medical industry. The cyclotron is designed to deliver alpha particles, carbon particles and other particles dedicated to the study. Each of these machines comes with specific characteristics discussed in detail in the literature review. The operating concept of the machine is based on an axial injection of particles under the influence of a strong magnetic force. The magnetic system of the 400MeV cyclotron has elliptical shapes and designed for optimal operational efficiencies. The system optimizes the use of magnetic fields and is designed to avoid instances of undesirable resonance.
Conclusion
In conclusion, cyclotrons are machines designed and developed for the purpose of accelerating ionized particles in a vacuum moving in a circular path. Typically, the mechanism of moving particles in a circular orbit is attained by positioning a strong magnetic field in the trajectory of the electrons. In addition to that, the path of the ionized particles is attained by the use of resonant accelerators. On the other hand, it is important to consider the fact that the energy of the moving particle can be enhanced to higher levels. In addition to that, there is a strong relationship between the gap voltages that enables ionized particles to move in a circular orbit and the speed and trajectory of the ions. The advent of the cyclotrons was based on the uniform field cyclotron with a vertical magnetic field defined by the positive field index.
Works Cited
Kim, Sang, W., Kwon, Duck-Wee, and Lee, Hai-Wong. Relativistic Cyclotron Motion in a Polarized Electric Field. Journal of the Korean Physical Society, 32-1. 1998.
Sabaiduc, V., Du, D., Boiesan. T. Zhu, J. Suthanthiran, K., Johnson, R.R., Ladysmith, Gyles, W., Gelbart, W., Z., and Conard. New High Intensity Compact Negative Hydrogen Ion Cyclotrons. n.d. Web.
Su, Q., Wagner, Peverly, P.J., and Grobe, R. Frontiers of laser physics and quantum optics: proceedings of the International Conference on Laser Physics and Quantum Optics.
Venturini, M.,. Kishek, R.A. and Reiser, M. “Dispersion and Space Charge”, Shelter Island Workshop on Space Charge, AIP Proc. 448. 1998. 278.
Vorobiev, L.G. and York ,R.C. “Analysis of the Injection Line for the University of Maryland Electron Ring Including Dispersion and Space Charge”. 1999. MSUCL- 1122.