Introduction
Newton’s second law is of fundamental importance to learning and understanding physics. This law states that the rate at which momentum of an object changes is proportional to the forces imposed and goes in the direction of the force. The law is represented by the formula F = Ma where F is the force applied in a particular direction, M is the mass of the object upon which the force has been applied, and ‘a’ is the acceleration in the direction of the force (Serway and Jewett 5).
The concept of Newton’s second law stems from mass and force applied on the same. Mass is the amount of matter in an object and is a scalar quantity meaning that it has no direction. The heavier the objects, the larger the mass of that object. When force is applied to an object, the object responds to the force based on its mass. A massive object responds slowly compared to a lighter object. When force is applied on an object, it becomes unbalanced if it does not meet an equally opposing force. As a result, there will be acceleration depending on the direction of force applied with an inverse relation to the mass of the object.
Newton’s second law of motion is vital in science because it aids in understanding behaviours of universe. The universe exerts its action through force and matter, which are important pillars that Newton’s second law provides a relation for the same. This relationship aids in summing up Newton’s three laws.
Weight and Mass
Mass is the quantity of matter in an object. It is a scalar quantity meaning that it has no direction. This implies that the mass of an object will be the same everywhere in the world and the outer space. Weight on the other hand is the measure of the force of gravity acting on the object. It is a vector quantity meaning that it has mass and direction. The gravity is a force that holds objects on the ground. If this force is weak, the weight of the object will be less since there will be less force holding the object. This implies that weight of an object changes with the change of place and is therefore not constant in the outer space (VanCleave 2).
If a one kilogram mass is attached to a spring balance on earth, it will read one kilogram. Moreover, if a mass of one kilogram on earth is placed on a beam balance, it will require a one kilogram mass on the opposite end to balance it. When the two experiments are carried out on the moon, the spring balance will read about 100 grams while the beam balance will still require the same amount of one kilogram weight to balance the mass on the other side. This denotes that mass is constant but weight varies.
Free fall vs. Terminal Velocity
When an object is in a free fall, it means that it is in the motion where there is no other force acting on it apart from the weight of the object. Based on the Newton’s second law of motion, it means that an object on free fall will continue to accelerate as long as they are falling freely. Since the gravity is the only force of acceleration on the object on free fall, it means that the object on free fall will accelerate with the same rate of 9.8 m/s2 despite the consequences of their mass. On the other hand, terminal velocity is a state attained by the object moving in a fluid when its force of drag acting on it equals the force of gravity acting on it. At terminal velocity, the object no longer accelerates but rather continues to move in the velocity it was moving in when it attained the terminal velocity (Serway and Jewett 10).
Newton’s second law of motion is given by the equation F = ma meaning that a = F/M. For a small object, F will be small and M will be small also. For a big object, F will be large and M will be large also. This means that the ration of ‘a’ will be the same for all objects. In free fall, the object is affected by both M and F. During the free fall, the only acceleration is a = F/M = 9.8 m/s2= gravitational force.
In addition, the net force of drag force acting on the object is given by mg – ½ pv2 ACd where p is the density, v the velocity, A is the area, Cd is the coefficient of drag, g is the gravitational acceleration and m is the mass of the object. The net force acting on the object is thus given by Fnet = ma= Newton’s second law = mg – ½ pv2 ACd at terminal velocity, the net force is zero. This mean that 0 = mg – ½ pv2 ACd and V becomes terminal. Solving for Vt gives Vt = 1/2
Simple Harmonic Motion
When an object in a state of equilibrium is slightly displaced from its point, it will oscillate from the equilibrium position. When displacement occurs, the object will experience a restoring force that depends on the displacement distance from the equilibrium point. An illustration is shown bellow
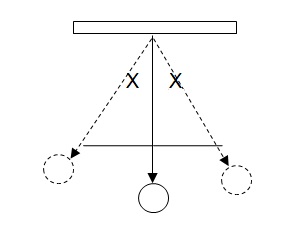
From the diagram above, the object is displaced by distance X from its equilibrium position. The motion repeats itself and is called simple harmonic motion. According to Hooke’s law, the restoring force F = KX where k is a constant of the material and X is the distance of displacement. Simple harmonic motion is mostly experienced in a springs. Simple harmonic motion is characterized by the two quantities; the frequency or period and the amplitude. In harmonic motion, the displacement is assumed to be small. And the resistance of air or the drag assumed to be zero.
There are some real life examples of simple harmonic motion in everyday life. One of them is the children play swing. The swing goes on and forth in a simple harmonic motion. When the child swings, he or she is restored by the force that depends on the weights of the child. This force is given by F = Mg.
Another example of real life example of simple harmonic motion is the pendulum clock. The pendulum of the clock swings on and forth in simple harmonic motions. The pendulum has a small weight of mass attached at the tip, which provides the restoring force to the pendulum (Snape 35).
Centripetal Force
Centripetal force is the force that holds an object in circular motion. Planetary bodies are in constant motion around the sun. The illustration is as shown bellow.
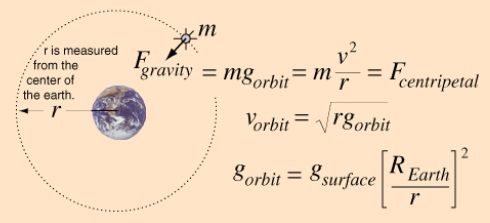
From the above diagram, the planets revolve around the sun and are held in place by gravitation force, which is the centripetal force. The force of gravity is given by F = Mg = mV2/R = centripetal force. The gravitational force tries to pull the earth towards the sun but the centrifugal force pulls the earth away from the sun leading to a balance. From the equation above, R is the radius of the orbit and thus the orbit in this case is assumed to be circular. This force is perpendicular to the motion of the planet and therefore the force of gravity does not work on the objects on orbit. However, in normal cases, the earth’s’ orbit is not circular as assumed by the equation above. The earth’s orbit is elliptical in shape. This is because the earth at rotates at its own orbit at the same time revolves around the sun’s orbit. During the cause of rotation, the centrifugal force of rotation makes the earth to bulge at the centre or to the equator (Russell. 4). As a result, the earth is elliptical in shape. The information is shown in the figure below.
The discoveries by Kepler that the earth’s orbit is elliptical led to scientific discoveries in the modern science. Prior to this, there were arguments that the earth was at the centre and the sun revolved around it. Important equations that are used in the modern science were formulated by Kepler. The first law of planetary motion that states that planets moves in elliptical orbits and the kepler’s second law that explains the relationship between the speed of rotation and the distance from the sun were formulated and are used in the current science. These discoveries led to the revolution of the science of the orbit that was propagated by Galileo. Further study into the same led to the modern science of the four seasons of the earth, which are influenced by the earth’s elliptical orbit (Afzal 8).
Works Cited
Afzal, Khadija. Why the earth is elliptical? Inforpedia. 2011. Web.
Russell, Randy. Elliptical orbits. Windows to the Universe. 2005. Web.
Serway, Raymond and Jewett , John. Physics for scientists and engineers. Cole: Brooks Publishing Press, 2004. Print.
Snape, Charles. Newton’s laws of motion. London: Cambridge University Press, 2010. Print.
VanCleave, Janice. Mass vs. weight.Sceince Fair Projects. 2010. Web.