Introduction
Among the household names in the scientific sphere that has formed the basis for contemporary scientific thoughts is Sir Isaac Newton. Indeed, great thinkers regard Newton as one of the elite polymaths to have ever lived as his contributions in an array of disciplines remain exceptional. His major contributions in fields such “as mathematics, physics, astronomy, theology, and chemistry did highlight him as a great thinker.” He was typically a genius, whose commitment to the unraveling of mysteries greatly affected his social life since he spent sleepless nights, do without his food, and skip his lectures.
Moreover, religious orientation depicts Newton as a rationalist because much of his studies skewed toward myth and alchemy. As one of the great scientists of the 17th century, Newton published his scientific theories and findings in the Principia, his masterpiece in the realm of science. In the Principia are the three laws of motion, which elucidate laws that govern the motions of objects in the universe. Therefore, this report examines the background of Newton’s life with a view of exploring his three laws of motions as defined in the Principia, while providing examples of their applications in real life.
Background of Newton’s Life
Newton existed from the mid 17th century to the early 18th century (1642 to 1727), which is a period of about 85 years. In his early life, Newton never lived to see his father because he died three months prior to his birthday in 1642. His parents were successful farmers, although his father, also called Isaac Newton, was uneducated. Faced with the challenges of growing up under a family situation of a single parent, his childhood and future seemed bleak. Since his dad died, his mother decided to remarry, and thus she left him under the care of his maternal grandfather because he never liked his stepfather. Consequently, Newton and his mother only reunited after the stepfather died.
Despite the experience of poor parenting, Newton managed to study and pursue his dreams. At the age of 12 years and 17 years, Newton learned Latin at The King’s School in Grantham. Although Newton wanted to forgo his studies, the master of King’s School persuaded him to continue, and thus he joined Trinity College in Cambridge after obtaining a scholarship. The college transformed his career because he managed to read the works of philosophers such as Aristotle and Descartes, and astronomers like Galileo. During his studies, Newton focused on optics, the law of gravitation, and mathematics, which later became the pillars of his discoveries in the realm of science. When he received his bachelors in arts, and subsequently, masters in arts, Newton succeeded his professor because of exemplary performance that he exhibited in college.
Before Newton defied the odds to emerge as one of the greatest scientists, who have ever lived, he faced many challenges. His early phase of his carrier was particularly very challenging. Aside from his illustrious life in the sphere of influence, Newton never married throughout the 85 years he lives on earth. He maintained a click of very few friends, with much of his time dedicated to his researches. Consequently, Newton experienced a number of nervous breakdowns.
In 1677-1678, Newton suffered the first nervous breakdown when he was at the age of about 35 years. Newton also experienced another severe nervous breakdown in 1693, which considerably affected his health. Newton’s professional life was very rough because he experienced massive challenges, which made critics fault his schools of thought. Nevertheless, in spite of the controversy, he occasionally harbored, he died a celebrated icon in his sphere of influence and commanded great respect from all people across the world. He died as a “wealthy man and had a lavish funeral ceremony at Westminster Abbey, where he is buried.” Chemical analysis of his hair after his demise showed that mercury poisoning could have contributed to his ill health and untimely death.
He was reluctant to publish his researches owing to the fact that much of his early discoveries attracted much criticism. His modest personality and enormous criticism complicated the exposition of his discoveries. Even the encouragement from the elite minds could not prompt him to publish his works. However, it took the support of Isaac Barrow, his professor, and other scientists to convince Newton to publicize his works. After his debut publication, one publication that has been a major highlight of his career was the Principia Mathematica.
Newton reframed the title of his publication from Philosophiae Naturalis Principia Mathematica, where he derived his three laws of motion to the Principia Mathematica, which has “become one of the most important and influential works on physics of all times.” Moreover, it is in this publication that he gave insights into elliptical orbits and the effects of forces on a body. It is noteworthy that Newton published his works on fluids and mechanics in the aforementioned publication.
The Principia Mathematica, which great thinkers dubbed the Principia, was a product of Newton’s industrious years of the mid-1660s. In the late 17th century, Newton had done numerous researches, and thus he managed to publish the Principia in 1687. This work considerably transformed the world because it acquired scientific recognition as “one of the world’s most important scientific treaties.” The Principia is a publication that made Newton rise to fame and rank as one of the scientific theorists of the 17th century. The Principia enlightened modern scientists it offers a novel perspective of science from physical and mathematical angles. Through the application of the scientific theories in the Principia, scientists were in a position to explain the motions of celestial bodies.
The emergence of the novel findings rendered many hypotheses and theories obsolete. Before the advent of the Principia, hypotheses and theories that explained the existence of orbits and revolution of planets around the sun were baseless since they were devoid of mathematical foundation (Calculus). This publication encompassed “works from other scientists like Johannes Kepler, a German, who discovered that planets’ orbits are elliptical in nature.” Moreover, he also gave vital information about orbital radii, and the period a planet takes to complete a revolution. However, his findings lacked mathematical foundation, and therefore, Newton seized the opportunity to incorporate mathematical principles.
By applying mathematical principles, Newton came up with a general theory of gravitation, which governs all bodies in the universe. Importantly, even with its revolutionary effect, very few scholars could comprehend the Principia during the 17th century. Not even Newton’s contemporaries could unravel the contents of the Principia and apply them empirically. The difficulties of understanding the contents of the Principia originated from the complexity of mathematical principles and intricacy of theoretical conceptions. However, the three laws of motion that stand out in the Principia are laws that elucidate the motions of objects in the universe. The discovery of the gravitational force enhanced practical application of three laws of motion in the study of universal forces.
Newton’s Laws of Motion
Newton’s First Law of Motion
Newton’s first law of motion dubbed as the law of inertia states that “an object at rest stays at rest and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced.” The Newton’s first law of motion is the law of inertia because it explains about the tendency of bodies or objects to resist change in velocity, both speed and direction. The existence of other forces influences movement of objects or bodies in terms of speed and direction. A resting body has neither speed nor direction, and thus it resists forces that compel it to speeds towards a certain direction.
Likewise, a moving body has both speed and direction, and thus it resists forces that compel it to slow, increase the speed, or change direction of movement. Hence, the first law of motion constitutes two clauses: one that defines bodies at rest and the other one that covers the bodies in motion. These clauses describe what happens when objects experience forces under different conditions of rest and motion. As an illustration, figure 1 below depicts these two clauses.
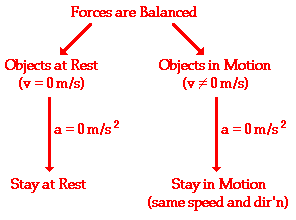
From the figure one, the first clause indicates that an object at rest has a zero velocity (v = 0 m/s). As the inertia requires balancing of forces, it holds that the object is always at rest, unless an external force compels it to change its velocity. Essentially, an object at rest has an inertia force that makes it resist the influence of external forces. Novice’s interpretation is that an object resists external forces that compel it to move from one place to another. Fundamentally, the clause depicts the Newton’s notion that an object maintains its position so long as external forces do not compel it to change velocity. Since velocity is a vector quantity, which has both speed and direction, a body at rest has zero velocity. This implies that both speed and direction are zero, which contrasts that of a moving body.
The other clause depicts an object in motion and velocity. For instance, a moving body at a velocity of 10 m /s, which has both speed and direction, has inertia force. According to the first law, a moving body has the ability to move continuously with constant speed in a specific direction if other forces do not influence it to act otherwise. The inertia of the body is dependent on speed and direction. This implies that a moving body resists change of speed and direction. For the moving body to change speed, it must encounter an external force. Similarly, for the moving body to change direction, it must encounter a force that compels it to do so. The fundamental condition of the first law is that unbalanced forces compel bodies to change their status: rest and motion. As the law of inertia, the first law elucidates resistance that bodies experience during rest or motion.
In the Principia, Newton’s typical words while framing the law states that, “everybody will stay in a state of rest or uniform motion in a straight line unless that state is changed by forces impressed upon it.” The law explicitly reveals two elements of velocity, which are ‘uniform speed’ and ‘straight direction.’ In real life situation, the first law is evident when one jumps out of a moving vehicle. When one is in a vehicle moving at a velocity of 40km/hr, it means that the person is also moving at the same velocity.
Jumping out of a vehicle that is moving at 40km/hr requires one to resist that speed or risk falling down. The direction in which one falls when jumping out of a moving vehicle is the direction of the vehicle. As per the first law, a person falls down because the body tends to move at the same velocity as the moving vehicle. However, the effort that one applies against inertia prevents one from moving at the same velocity as the vehicle. Furthermore, another example is that when a stationary vehicle moves quickly, people jerk back because they resist motion. Thus, these real life scenarios depict the instances where the first law of motion is evident.
Newton’s Second Law of Motion
The first law of motion forms the foundation of the second law because Newton supposes that either an object is at state of rest or in motion. Essentially, bodies that the first law governs have constant velocity. Since objects in the universe experience numerous unbalanced forces, Newton tries to understand the behavior of these objects. As per his thoughts, an object will experience acceleration or deceleration once there is a net force compelling it to act differently. From the equation below, Newton depicts acceleration or deceleration as derivative of velocity.
F = m![]() = ma
= ma
From the equation, F = force, m = mass, v = velocity, a = acceleration or deceleration.
The second law of motion indicates that mass and acceleration or deceleration determines forces that bodies have in their motion. Mass and acceleration have negative correlation because an increase in one leads to a decrease in the other. According to the Principia, Newton states that the “size of the acceleration is directly proportional to the force applied, and inversely proportional to the mass of the body.” Fundamentally, when a body increases velocity over a certain period, it accelerates, while it decelerates when it reduces velocity over a specific period. Figure 2 below depicts how unbalanced forces occur and how they influence acceleration or deceleration of bodies.
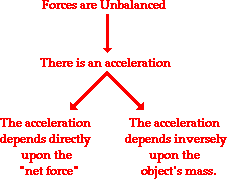
The equation below provides the mathematical interpretation of the law — Acceleration = Net Force /mass or a = F/m
The above equation can be rearranged such that the net force becomes the subject formula i.e. Fnet = ma
The above equation represents the equation of the second law of motion, which forms the basis of many calculations. Given that acceleration is a vector quantity, it values can either be negative of positive figures, which depict deceleration or acceleration respectively. Ideally, the sign of the force acting on the body does not take an arbitrary sign, but it assumes a vector quantity.
The equation of the second law agrees “with the definition of a unit force which is given as the product of a unit mass and unit acceleration.” When put in equation form using the international systems of units, the equation below emerges.
1 Newton = 1 kg × 1 m/s2
As such, one Newton is “defined as the amount of force required to give a 1-kg mass an acceleration of 1 m/s/s.”
One important application of the second law of motion in real life happens when one is pulling or pushing a cart. The velocity and direction of the cart depend on the effort applied to it (Force). The amount of force applied just before the cart starts to move has zero acceleration. However, when one pulls the cart, a net force that makes the cart move and causes it to accelerate exists. Thus, acceleration of the cart is dependent on the amount of force exerted on it.
Newton’s Third Law of Motion
Fundamentally, the third law of motion holds that reaction force is equal to the action force. To experience “its effect, there is need for interaction between two objects.” When object A exerts a certain force on object B, it experiences same quantity of force from Object B. This means that interacting forces are equal, but they act in opposite directions or against each other. According to Newton, “this pair of forces is called action and reaction forces.” The opposing forces are equal in magnitude because they do not only act against each other, but are also dependent on one another. Hence, in the third law of motion, Newton explores the relationships between a pair of forces and affirms that they are equal and opposite.
In his book the Principia, Newton frames the third law of motion by postulating that, “for every force applied to a body, there is an equal and oppositely directed force exerted in response.” Simply put, when two bodies interact, they exert against each other equal magnitude of force, which act in opposite directions. Therefore, the third law of motion indicates that when two bodies interact, none experience greater pressure or force than the other. This law depicts how bodies interact and experience similar forces, which are action and reaction forces.
The third law of motion has numerous practical applications in life, which have transformed the lives of humans. One of the major applications of the third law of motion is in construction of rocket engine or jet engine. The principle behind the rocket or jet engine is that of the third law of motion. The motion of rocket or jet is dependent on thrust that it generates from the combustion of fuel. The combustion of fuel and their release with a very high pressure constitute an action force.
Comparatively, the thrust that a rocket or jet gain is a reaction force that emanates from the combustion of fuel. Hence, the pressure that combustion of fuel generates is equal to the thrust that rocket or jet gains. Another example is the principle that the firing of a gun uses. During firing of a gun, trigger sparks fire, which causes gunpowder to explode and cause massive pressure. The pressure propels the bullet forward with a very a high speed that is commensurate to the force of the gunpowder explosion. In essence, the action of the gunpowder explosion is equal to the reaction of bullet propulsion.
Among living organism, third law of motion is evident in the manner in which a fish swims. What happens is that the fish’s fins pushes water in a backwards direction (action). Consequently, the water molecules accelerate backwards resulting in a backward force. The backward force generates and equal and opposite force (reaction) on the fish, resulting in acceleration, which propels the fish forwards. The process recurs and causes propulsion of fish further forwards. Furthermore, a bird on flight exhibits the principle of their law of motion. To fly high, the wings of a bird must interact with the air molecules. Ideally, whatever happens is that the wings push the air molecules backwards (action), and hence, cause them to accelerate backwards. The forward force emerges as a reaction force to the backwards force. Thus, the action and reaction forces of flight recur as long as the bird keeps on pushing the air molecules backwards.
Conclusion
Sir Isaac Newton is among the celebrated personalities, who have made significant contributions in a wide scope of disciplines. His contributions have truly metamorphosed a scientific perspective of the universe. As such, through his ideas, scientists have solved many mysteries and his principles continue to dominate various realms of knowledge in modern society. His ideas solely took scientific thinking to new heights, where now ‘reason’ rather than ‘hypothesis’ dominates a scientific explanation. Importantly, he came to the public limelight following the publication of his book, Philosophiae Naturalis Principia Mathematica (1687).
In his masterpiece, the Principia, Newton elucidates the three laws of motion, which govern the movement of objects in the universe. In the first law, Newton postulates that a body upholds its state of motion/rest unless compelled to do otherwise, while in the second law of motion, Newton states that force is subject to mass and acceleration of a body. The third law focuses on the interactions of force and asserts that action and reaction forces are equal although they act in opposite directions. Analysis of these three laws of motion shows that they are applicable both in the movement of animals and objects.
References
C. Maclaurin, An Account of Sir Isaac Newton’s Philosophical Discoveries (Millar and Nourse Publishers, London, 1970), pp. 4. Web.
C. Martins, Sir Isaac Newton’s Mathematical Principles of Natural Philosophy and His System of the World (University of California Press, Berkely, 1934), pp. 34. Web.
I. Newton, The correspondence of Isaac Newton, (Cambridge University Press, Cambridge, 1940), pp. 10. Web.
J. Deighton, Isaac Newton’s Papers and Letters on Natural Philosophy and Related Documents (Cambridge University Press, Cambridge, 1958), pp. 12. Web.
J. Edleston, Correspondence of Sir Isaac Newton and Professor Cotes, including letters of other eminent men (New York University Press, New York, 1990), pp. 8. Web.
R. Cotes, The Unpublished Scientific Papers of Isaac Newton (Cambridge University Press, Cambridge, 1962), pp. 5-8. Web.
S. Thayer, Newton’s Philosophy of Nature: Selections from His Writings (Liverpool University Press, Liverpool, 1980), pp. 122. Web.
T. Parker, Isaac Newton’s ‘Theory of the Moon’s Motion’ (Dawson, London, 1975), pp. 90. Web.
T. Whiteside, The Mathematical Papers of Isaac Newton (Cambridge University Press, Cambridge, 1999), pp. 32. Web.