One-Way Between-Group Analysis of Variance Essay

Basic One-way ANOVA Study

One-way between-group analysis of variance (One-way ANOVA) applies in cases in which there are independent variables or groups with three or more groups or levels and one dependent continuous variable (Pallant, 2005). One-way implies that the question only has one independent variable while the measure between groups implies that there are various subjects or cases in every group.

One-way ANOVA must meet the following assumptions to make it acceptable(Jackson, 2012):

• Independent samples.
• Normal distribution of responses.
• Equal variances of subjects.
• Independent responses.

An appropriate research question that would require the use of a one-way

• Is there a difference in consumption scores for young, middle-aged, and adult subjects who consume alcohol?

Why this question is appropriate for the selected statistical test

This question is appropriate for one-way ANOVA analysis because it captures the vital conditions required for this type of statistical analysis.

• It has one categorical independent variable, which has three different groups. They are continuous variables that capture three equal groups. The focus is on the age group of the research subject. For instance, we can have three categories of the subjects’ age group: between 18 and 24 as younger, between 25 and 30 years as middle-aged subjects, and between 31 years and above as adult subjects.
• The question also has one continuous dependent variable (the rate of consumption scores).

From this question, the researcher would show whether there are significant differences in the mean scores of the dependent variable in all the three age groups of alcohol consumers.

The variables in this study and each of their attributes

• Continuous categorical independent variable (age group of the research subjects)

Age group is measured on a nominal scale.

• Continuous categorical dependent variable (the rate of consumption scores)

This would also take a nominal scale of measurement.

Do the variables fit the qualifications for the selected statistical test?

Categorical independent variable

Categorical variable assumes one of a restricted and normally fixed number of a given value. The age groups of respondents are limited and fixed within a group of alcohol drinkers.

Continuous dependent variable

We have created infinite numbers with various values between two points of a scale to measure alcohol consumption among young, middle-aged, and adult participants.

Categorical variables are also known as nominal variables. They have two or more categories without intrinsic order. We simply assigned age categories of respondents in various groups.

The researcher will be able to manipulate the categorical independent variable to observe changes that will take place. For instance, manipulation of subjects’ age would have effects on the rate of alcohol consumption among subjects. If no change takes place, then there would be no response in the continuous dependent variable.

The statistical notation and written explanation for the null and alternative hypotheses

Notation for a linear model:

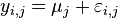
(Means model) or

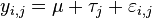
(Effects model)

• In which i = 1, …, I
• is experimental groups j = 1, …, J
• is manipulated, groups I_j
• is the number of experimental groups in the j^th manipulated group

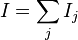
is aggregate of experimental groups yi,j = observed changes μi = the mean of the observed changes for the j^th manipulated group μ = grand mean of the responses τi = the j^th manipulated effect

∑τi=0, μi = μ, ε∼N(O, σ²), εi,j is normal distribution zero-mean random error.

Hypotheses

• H₀: There is no difference in consumption scores for young, middle-aged, and adult subjects who consume alcohol.
• H₁: There is a difference in consumption scores for young, middle-aged, and adult subjects who consume alcohol.

References

Jackson, S. L. (2012). Research methods and statistics: A critical thinking approach (4^th ed.). Belmont, CA: Wadsworth.

Pallant, J. (2005). SPSS Survival Manual. Sydney: Ligare.