Introduction
There are ten stocks in the portfolio, including Amazon, Inc., Intel Corporation, Twitter, Inc., Visa, Inc., Nokia Corporation, Ford Motor Company, Chesapeake Energy Corporation, Universal Forest Products, Inc., Tesla, Inc., and MKS Instruments, Inc. The reasons for selecting these stocks are their recent price gains and positive financial news. The stock performance and its volatility of all stocks are provided in the following.
Table 1. Stock Performance and Volatility.
Main body
It is noted that the top performer was Chesapeake Energy Corporation, and the bottom performer was Amazon, Inc. on a monthly return basis. However, Amazon had the highest stock gain of 425.86% over the five years, and Chesapeake Energy Corporation made the most significant stock loss. The highest volatility was recorded in the stock value of Chesapeake Energy Corporation, and the lowest was of Visa, Inc. The S&P 500 index had an average monthly loss of -0.5723% over the last five years (see table 1). Its volatility was 0.03483, which was less than all stocks included in the portfolio that implies that it is well-diversified, and investors will be exposed to lower risk if they have an investment in all 500 stocks.
The correlation matrix between all the stocks over the past five years is provided in the following.
Table 2. Correlation Matrix.
Table 2 indicates that the coefficients of correlations between AMZN and V and INTC and MKSI are more than 0.6 (see table 2). It could be due to the close relationship between these companies. There is a significant number of business transactions on Amazon’s e-commerce website, which is paid by users using VISA credit cards. Moreover, Intel, Inc. and MKS Instruments have similar businesses related to products/equipment used by other companies and industries. There are three combinations of companies’ stocks, including CHK/TWTR, CHK/NOK, and TSLA/F, which have small coefficients less than 0.1 (see table 2).
It implies that these companies are entirely unrelated to each other. For example, Tesla and Ford Motor Company are competitors, and their stocks are not correlated. The coefficient of TSLA/UFPI is negative (see table 2), which cannot be explained as both companies are operating in different industries and are not related to each other at all. The covariance matrix is provided in Appendix A. The optimal portfolio is created by determining the lowest value of the portfolio variance. In this case, short-selling is allowed, and the results are provided in the following:
Table 3. Optimal Portfolio.
The lowest value of portfolio variance is 0.0014, and the expected portfolio return is -0.64% (see table 3). The weight of each stock is provided in the following.
Table 4. Stocks’ Weightage (No Short Sale).
The highest weight is assigned to Visa, Inc., and no allocation of funds is made to AMZN, TWTR, CHK, UFPI, and MKSI (see table 4). The weight does not seem reasonable as it left out stocks such as AMZN, TWTR, and MKSI, which had significant growth rates recorded over the last five years. I will be reluctant to present this portfolio choice to a client. The minimum variance frontier is given in the following.
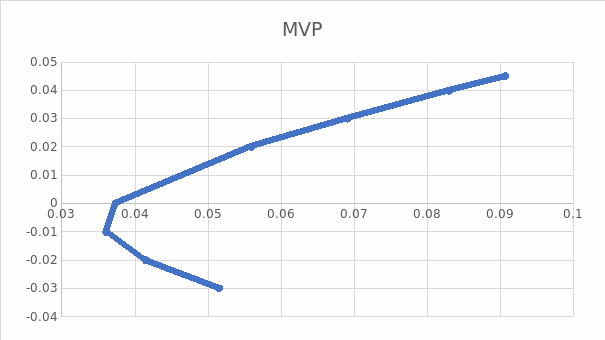
The expected return is nil when the standard deviation is 0.037 (see figure 1). The use of historical information as inputs to portfolio theory is useful in many ways. The historical stock returns are crucial to determine the performance of stocks over a period. It is the primary indicator observed by investors when making their decisions about investing in stocks. The primary objective of an equity investment is to maximize the expected return.
If a firm has poor stock performance in the past, then investors will be reluctant to invest in its stocks. The covariance between stocks assists in determining which stocks to be included in the portfolio. It is a statistical measure used by portfolio theory to lower the overall risk. It is also suggested that stocks that have a negative covariance with each other reduce the portfolio risk. Negative covariance, as it has been noted between TSLA and UFPI, is a good indicator and suitable for developing an efficient portfolio. It can help in creating an efficient portfolio of stocks that can optimize the portfolio return at a low level of risk.
It is stated that the standard deviation is a measure of the systematic risk of investing in an individual stock. Its use by portfolio theory helps in understanding how investors can reduce the degree of investment risk by reviewing the historical data and then choosing stocks that have lesser volatility. The criticism of the Modern Portfolio Theory lies in its use of historical data, which states that it is difficult to select a representative subset of historical data to use. Moreover, there may be certain economic events in the past that could have distorted the trend in the stock return.
If no short sales are allowed, then the optimal portfolio is achieved where the Sharpe Ratio value is the highest (see table 5).
Table 5. No Short Sale Allowed.
The weight assigned to each stock is provided below:
Table 6. Stock Weightage.
When this is compared with the previous optimal portfolio, it is noted that the allocation to INTC, TSLA, and F is reduced to zero. On the other hand, funds are allocated to stocks, including TWTR, CHK, and V, which had zero allocation in the previous portfolio. Furthermore, investment in NOK is increased, and still, no allocation is made to AMZN (See table 6).
I decided not to invest in Nokia because of its misleading advertising case reported in 2012 as it attempted to deceive its customers by using false imagery in its advertisements. Furthermore, I excluded Chesapeake Energy Corporation as it was involved in a land price manipulation case. The following optimal portfolio was achieved without these two stocks.
Table 7. Green Listing.
Conclusion
In this case, the Sharpe Ratio is 0.3650 (annualized) (see table 7), as compared to 1.1777. It implies that this portfolio is more efficient than the previous one. Moreover, the weight assigned to each stock is given below.
Table 8. Stock Weightage (Green Listing).
The cost of the above portfolio is determined by using the current price of these stocks along with their allocation (see table 8).
Table 8. Portfolio Cost.
It is noted that the value of the portfolio has reduced from August 8, 2019, to October 25, 2019 (see table 8).